
- •1.Математичне сподівання дискретної випадкової величини та його властивості
- •2.Помилки першого і другого роду при перевірці гіпотез.
- •1.Нормальний розподіл
- •2. Нелінійна кореляція??
- •1.Локальна теорема Лапласа
- •2.Перевірка гіпотези про нормальний розподіл генеральної сукупності
- •2. Метод найбільшої правдоподібності
- •Властивості
- •Статистичне визначення ймовірності
- •1.Геометрична ймовірність (Також Варіант 21,№ 1)
- •[Ред.] Використання геометричної ймовірності
- •1Інтегральна формула Пуассона
- •2. Метод найбільшої правдоподібності
- •2,Точкова оцінка
- •[Ред.] Визначення
- •[Ред.] Властивості точкових оцінок
- •1. Формула Байєса
- •Наслідок
- •2. Задача математичної статистики
- •3. Дисперсія та її властивості
- •Властивості
- •4. Основний принцип перевірки статистичних гіпотез
- •5. Показниковий розподіл
- •Квантилі
- •6. Коефіцієнт кореляції, перевірка його значущості Коефіцієнт кореляції
- •Властивості
- •7. Функція розподілу та її властивості
- •Властивості
- •8. Перевірка гіпотези про нормальний розподіл генеральної сукупності
- •Теорема додавання ймовірностей несумісних подій:
- •2.Способи представлення статистичного матеріалу:???
- •1.Рівномірний розподіл:
- •2.Знаходження параметрів прямої регресії:
- •1.Локальна теорема Лапласа:
- •2.Числові характеристики розсіяння:
- •1.Теорема множення ймовірностей:
- •2.Точкові оцінки:
- •1.Формули Байєса:
- •2.Метод моментів:
1.Геометрична ймовірність (Також Варіант 21,№ 1)
Матеріал з Вікіпедії — вільної енциклопедії.
Перейти до: навігація, пошук
Геометрична
ймовірність
– це поняття ймовірності,що запроваджується
так: Нехай
![]() -
деяка підмножина прямої, площини чи
простору. Випадкова подія
-
деяка підмножина прямої, площини чи
простору. Випадкова подія
![]() -
підмножина
.
Тоді ймовірність випадкової події
визначається формулою:
-
підмножина
.
Тоді ймовірність випадкової події
визначається формулою:
![]() де
де
![]() -
довжина, площа чи об’єм множин
та
.
-
довжина, площа чи об’єм множин
та
.
Це пов'язане з інтерпретацією ймовірності як міри на обраному просторі елементарних подій. В даному випадку він збігається з eвклідовим простором.
[Ред.] Використання геометричної ймовірності
Голка Бюффона: Яка ймовірність того, що голка кинута на поверхню розграфлену паралельними прямими розташованими через однакові проміжки перетне одну з цих прямих?
Парадокс Бертрана: Яке матсподівання довжини випадково обраної хорди на одиничному колі?
Яка ймовірність того, що три випадково обрані на площині точки формують гострокутній трикутник?
Та подібні...
Варіант 23
1Інтегральна формула Пуассона
Матеріал з Вікіпедії — вільної енциклопедії.
Перейти до: навігація, пошук
Інтегра́льна
формула Пуассо́на
Нехай для гармонічної
в кулі функції u(r,
φ) поставлена умова
рівності на границі функції u0:
u(R,
φ) = u0(φ),
при цьому функції належать наступним
класам гладкості:
![]() ,
де ∂D
— границя кулі D,
а
,
де ∂D
— границя кулі D,
а
![]() —
його замикання. Тоді розв'язок такої
задачі Діріхле можна представити через
інтеграл Пуассона:
—
його замикання. Тоді розв'язок такої
задачі Діріхле можна представити через
інтеграл Пуассона:
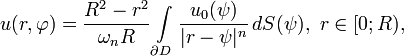
где ωn — площа одиничної сфери, а n — размірність простору.
2. Метод найбільшої правдоподібності
Визначення. Нехай є деяка сукупність x º (x1 ,…, xn) спостережень. Розглянемо імовірність (чи щільність) p(x/a) одержати це x при різних a º (a1 ,…, a). У якості оцінки візьмемо те значення а, для якого імовірність p(x/a) максимальна; такий спосіб оцінювання називається методом найбільшої (максимальної) правдоподібності.
Функція p(x/a), що розуміється як функція від а, називається функцією правдоподібності. Значення а*, при якій досягається максимум функції правдоподібності, називається оцінкою найбільшої (максимального) правдоподібності:
p(x/a*) = p (x/a). (4.2)
Помітимо, що а* є функція спостережень х: а* = а* (х). При звичайних умовах регулярності максимум знаходиться із системи рівнянь
i = 1, …, R. (4.3)
Приклад 4.1. Нехай х º (х1, …, xn) – незалежні спостереження над випадковою величиною, нормально розподіленої з параметрами b і s2 (роль двовимірного параметра а у визначенні грає пари b і s2 ). Щільність розподілу вибірки дорівнює
p(x/ b, s 2) º p(x1, …, xn /b, s 2) = . (4.4)
Оскільки значення х1 ,…, xn відомі, величина p(x1, …, xn/b,s2) є функцією від b і s2. Розглянемо систему:
Розв’язок цієї системи, тобто оцінки найбільшої правдоподібності:
Варіант 21
1.див(в25,№ 1)
2,Точкова оцінка
Точкова оцінка у математичній статистиці — це число, що обчислюється на основі вибірки, імовірно близьке оцінюваному параметру популяції.
[Ред.] Визначення
Нехай
![]() —
випадкова вибірка з розподілу,
що залежить від параметра
—
випадкова вибірка з розподілу,
що залежить від параметра
![]() .
Тоді статистику
.
Тоді статистику
![]() ,
що набуває значення в
,
що набуває значення в
![]() ,
називають точковою оцінкою параметра
,
називають точковою оцінкою параметра
![]() .
.
[Ред.] Властивості точкових оцінок
Оцінка
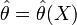 називається
незміщеною,
якщо її математичне
сподівання
дорівнює параметру генеральної
сукупності, що оцінюється:
називається
незміщеною,
якщо її математичне
сподівання
дорівнює параметру генеральної
сукупності, що оцінюється:
![]() ,
,
де
![]() позначає
математичне сподівання за припущення,
що
—
істинне значення параметра (розподілу
вибірки
позначає
математичне сподівання за припущення,
що
—
істинне значення параметра (розподілу
вибірки
![]() ).
).
Оцінка
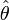 називається
ефективною,
якщо вона має мінімальну дисперсію
серед всіх можливих незміщених точкових
оцінок.
називається
ефективною,
якщо вона має мінімальну дисперсію
серед всіх можливих незміщених точкових
оцінок.Оцінка
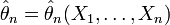 називається
конзистентною,
якщо вона за
ймовірністю
зі збільшенням обсягу вибірки
називається
конзистентною,
якщо вона за
ймовірністю
зі збільшенням обсягу вибірки
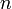 прямує
до параметра генеральної сукупності:
прямує
до параметра генеральної сукупності:
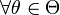 ,
,
![]() за
ймовірністю
при
за
ймовірністю
при
![]() .
.
Оцінка
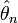 називається
строго
конзистентною,
якщо
,
називається
строго
конзистентною,
якщо
,
майже напевне при .
