Приведений до валу двигуна момент інерції приводу

•^ТТП=^ТТ+«^П+

^/л + Пптьг ’ ^ ТІТТсГ * ( ^б/п І І² +

ч2

^,пр~*^/д^-г*^/р"^г 7-2 ^ ^ПШК ’ ^и ШК ’І У 7)

/І V / ^ІЖ-⁷ /

+ (2-^ + ОТз +т_К)-\^/і²;

1п_Р = 4.5 + 4 +¹²⁰%₅2 + 6 • 1000 ■ (%₈)²/^{252 +}

+ (2 • 7 + 9 + 2.3) • 10³/25² = 62.77 кг • м²;

Кутове прискореня двигуна

є = а • / ; є = 0.6 ■ 25 = 15 рад/с² ,

Момент двигуна, який забезпечить рівноприскорений рух скіпа М = М_с + /_пр • є ; М = 4085.7 + 62.77 ■ 15 = 5027 Н • м .

27. Для механізму, кінематична схема якого зображена на рис. 1.13, визначити момент двигуна, необхідний для забез­печення в період розгону середньго прискорення а — 1.5 рад/с². Знайти також зусилля в канаті без врахування і з врахуванням його жорсткості.

Вихідні дані для розрахунків: маса вантажу т₁ = 5000 кг; маса противаги т₂ = 3500 кг; момент інерції привідного двигуна J = 3.2 кг . м²; момент інерції редуктора, приведений до швид-

кохідного вала J =2.8 кг . м²; # момент інерції барабана У, = 500 кг. м²; діаметр барабана Х)₆ = 2.0 м; передавальне чис- ло редуктора і = 20; ККД пе- редач _л = 0.8; жорсткість од- ного метра канату с = 6 .10 ⁷ Н; довжина канату = 300 м.

1.28. Визначити, з яким прискоренням буде опуска- тись вантаж т_х у механізмі,

кінематична схема якого зображена на рис. 1.13, якщо привід- ний двигун вимкнути з мережі, а механічне гальмо не буде працювати. Дані механізму наведені в задачі 1.27.

1.29. Визначити, як буде змінюватись швидкість і амплітуда коливань підвішеного вантажу при

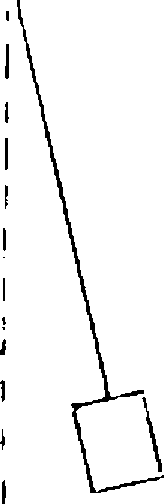
розгоні візка крана (рис. 1.14), та величину моменту, який повинен розвивати двигун, щоб зменшити амплітуду коливань вантажу в два рази.

Вихідні дані для розрахунків: маса візка т. = 7000 кг; маса ван- тажу т₂ = 14000 кг; довжина під- віски / = 4.0 м; жорсткість 1 м ка- нату с = 5.10⁵ Н; момент інерції двигуна і зв’язаних з ним обер-

тальних частин / = 0.3 кг. м²; передавальне число редуктора / = 20; діаметр ходового колеса візка = 0.5 м; середній момент двигуна М = 100 Н . м; момент статичного опору М = 30 Н . м.

де с

Втратами в передачах знехтувати.

—

□

Рис- 1.13

V.

СП

Д'10

Г

ї

Рис. 1.14

Розв’язок

Розрахункова модель, виконана відносно лі нійної швидкості V, наведена на рис. 1.15.

Радіус приведення параметрів

Я

—^ЛЛ^-

т

т

Рс

Рис. 1.15

О

0.5 2 • 20

к

= 0.0125 м

Р =

Р =

2-і ⁵

Приведене зусилля від моменту двигуна

F = Mæ. ; F = ¹⁰⁰ = 8000 H . p ’ 0.0125

Приведене зусилля від статичного моменту

^F‘-T’

Приведена маса двигуна

т„ _зв = ; »ід зв = ——у = 2 • 10³ кг. ^дзв р² ’ ^д 0.0125

Сумарні приведені маси

^ т = от_д зв + т_в + т ; ^ _т = 2000 + 7000 +14000 = 23 • 10³ кг ;

^т\ ^{= т}А зв ^{+ т}в ? = 2000 + 7000 = 9 • Ю³ кг .

Середнє значення прискорення

F-Fç 8000 - 2400

а =

_Z ; а = —— = 0.24 м/с² .

т ’ 23000 ⁷

Жорсткість канату

С_к = Т ; ^СК = ^- = 25 • 10³ Н/м .

*1

Частота коливань

т „ /25 -10³ - 23 • 10³

^Q = і ч— Г = 2-1 1/с.

¹¹ 9 -10 • 14 -10

Щ-Щ

Швидкість переміщення v₂ = а • і - (a/Q) • sin Qf ; v₂ = 0.24 * ґ — 0.114 - sin 21t. Величина відхилення вантажу

As = J v_xdt - J v₂dt = - ^{a mi} cos Qt.

А

з

25 • 10

а - т₂ .

^ск

30. Скласти розрахункову модель, знайти момент М,, що передається через вал 2 (рис. 1.16), та коефіцієнт динамічного перевантаження £_д при таких умовах: вхідний момент М = const

м

п.

М&х

(}.К

Рис. 1.16

= 120 Н. м; момент інерції двигуна = 0.4 кг.м²; момент інерції передачі JT_V приведе­ний до валу двигуна, /_п] = 0,2 кг. м²; момент інерції передачі Д,, приведений до валу механізму, /,= 18.0 кг.м²; момент інерції

D

механізму J_K = 80 кг.м². ККД передач: _Лі = 0.92, т,, = 0.9; пе­редавальні числа: і = 4.0, /, = 5.0; жорсткість другого валу с, = 8.10⁵ Н.м; момент статичного навантаження механізму М_и = 800 Н.м.

30. Ч^! ■ II¹' •

    р шшш?/////;///

    Рис. 1.17

    Визначити, який момент повинен розвивати кожен із двигунів приводу механізму поворотної платформи екскава­тора, кінематична схема якого наведена на рис. 1.17, щоб забез­печити її розгін з постійним прискоренням _є = 0.05 рад/с². Виз­начити також момент, який передається через вал 1 і коефіцієнт динамічного перевантаження, якщо жорсткість цього вала с₂ = 8.10³ Н .м /рад, а люфт передачі, приведений до валу двигуна, становить _п радіан.

Параметри привідних двигунів і пе­редач однакові. Момент інерції кож­ного приводного двигуна / = 30 кг.м²; момент інерції поворотної платформи зі всім обладнанням J_m = 16 0.10⁶ кг. м²; передавальні числа передач: = 20, і₂ = 25; ККД першої передачі (з і]) ^ = 0.92, другої передачі (з і₂) ^ = 0.9; момент статичного опору на валі двигуна становить 10% від динамічного моменту. Момент інерції редукторів не враховувати і вважати, що втрати в редукторі пос-

тшні и не залежать від статичного навантаження.

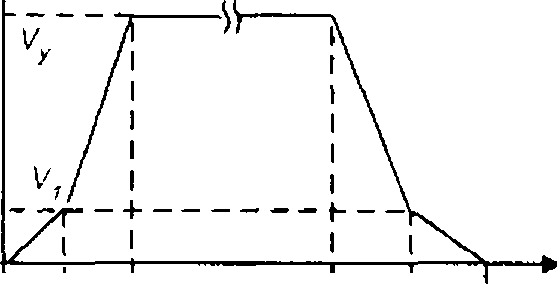
30. Для шахтного підіймача (рис. 1.7) з задан грамою руху (рис. 1.18) побудувати навантажувальну

16

механізму (діаграму зусиль у підіймальному канаті), якщо відомі такі параметри: швидкості руху кліті \\ =1.5 м/с, V = 4.5 м/с; допустиме прискорення в інтервалі часу ^ дорівнює 1.1 м/с², а в інтервалі - 4.1 м/с²; висота підіймання Н — 800 м; маса вантажу т_? = 6 ,10⁵ кг; маса кліті т,= 5.10⁵ кг; маса одного метра підіймального канату р = 3.1 кг; маса од- ного метра зрівноважувального канату q = 2.6 кг; довжина підіймального канату /. =

V

« Чи *

І І

Рис. 1.18

800 м; довжина зрівноважувального канату / = 800 м; маса обертових частин механіз­му, приведена до швидкості підіймального канату, т_у = 9500 кг.

Розрахунок статичного зусилля в канаті ведеться за фор­мулою:

Г = к • т • ё + (р - д) ■ (Н - 2Н_Х) ■ g (Н) ;

де к - коефіцієнт шахтних опорів, (можна прийняти £=1.1 ^1.2);

• - прискорення сили тяжіння; к - шлях, що пройшла кліть з початку підіймання.

а.

30. Розрахувати і побудувати графік зміни моменту елек­тродвигуна, який би забезпечував виконання тахограми руху механізму (задача 1.32), якщо момент інерції двигуна / = 4.15 кг.м², усталена швидкість обертання двигуна = 800 об/хв, ККД передач _л = 0.75.

31. Визначити момент на валі барабана в період розгону підіймача (задача 1.32), якщо момент інерції барабана / = 800 кг . м², його діаметр В₆ = 2.5 м.

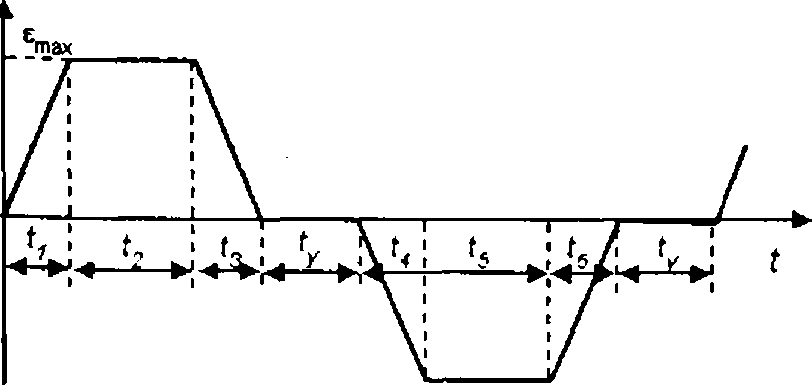
32. Нарис. 1.19 наведена діаграма зміни прискорення _є при розгоні та гальмуванні електроприводу. Розрахувати та по­будувати тахограму і діаграму зміни моменту двигуна, яка забез­печує задану діаграму прискорення. Тривалості часу на діаграмі:

⁽1 ^{= =} К = и = ² с; *2 = и = 4 с;

час ро боти на усталеній швидкос­ті ґ = 8 с. Сумарний приведений до вала двигуна момент інерції приводу /_р = 2.4 кг.м²; макси­мальне прискорення _Єіша = 50 рад/

с²; момент статичного опору М_с Рис. 1.19 =25 Н.м.

30. Визначити, як змінюється статичний момент на валі барабана шахтної підіймальної установки (рис. 1.20) зі змінним радіусом навивання канату в залежності від кута повороту барабана _ф. А саме, який буде статичний момент М_с при таких кутах повороту барабана: _фі = 0, у₂ = _фш /2, = _фш; де <р_ш - максимальний кут повороту, який забезпечує підіймання вантажу на задану висоту Ь.

І

д

Д - двигун Р - редуктор В - барабан К *■ кліть

т*т₉ + т_к

Рис. 1.20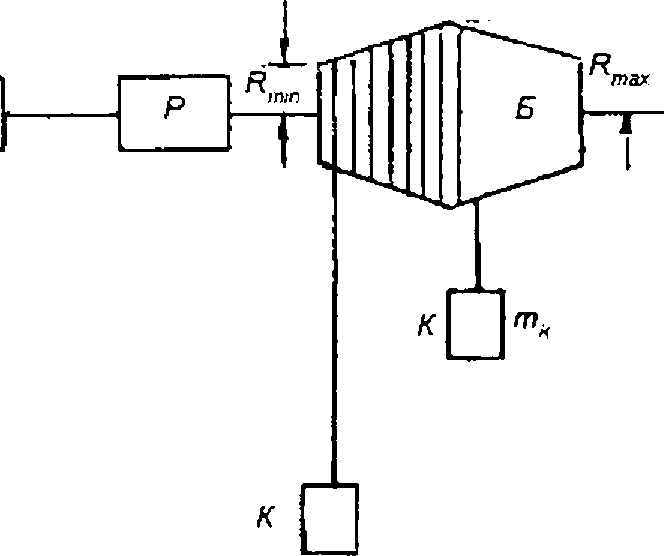

Вихідні дані: Маса вантажу т_ъ = 3000 кг, маса посудини т_в = 3500 кг, подовжинна маса канату р_т, = 3.1 кг/м, висота під-

л

німання Ь = 350 м, мінімальний радіус барабана Я_тіл = 1.5 м, мак­симальний радіус барабана і?_тах =

5. м.

30. Визначити момент на валі двигуна шахтної підіймальної установки (рис. 1.20) в кінці роз­гону до усталеної швидкості, якщо прискорення барабана при розгоні постійне і рівне 0.5 рад/с², усталена швидкість обертання двигуна п_у = 420 об/хв; передавальне число редуктора / = 11, момент інерції барабана X = 560 кг.м², ККД передач _л = 0.9.

31. Нарис. 1.21 наведена кінематична схема і тахограма руху робочих рольгангів. На відрізку 0-1-2 тахограми рольганг переміщує металеву заготовку, на відрізку 3-4 гальмується без заготовки. Розрахувати і побудувати навантажувальну діаграму двигуна. Вихідні дані: маса переміщуваного металу т_и = 4.10⁵

а)

б)

Д - двигун П - редуктор Т - трансмісія Р- ролик

V

Рис. 1.21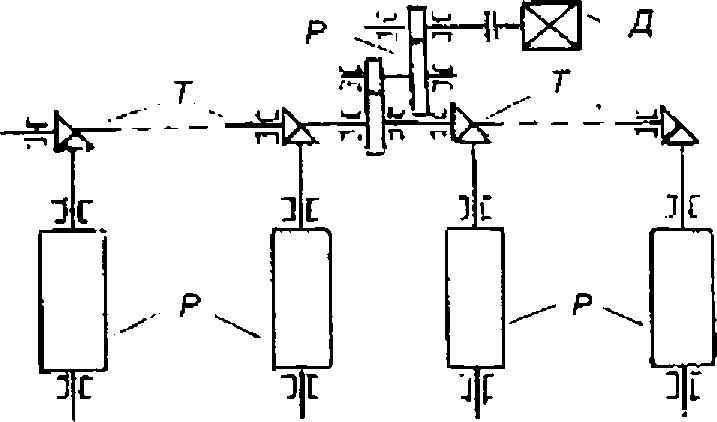

кг; максимальна швидкість пере­міщення т_тах = 3 м/с; шлях пере­міщення / = 6 м; кількість роликів к_? = 6; момент інерції ролика ^ = 70 кг.м²; ККД редуктора при навантаженні _Пі = 0.9, а при не­робочому ході _Л2 = 0.5; переда­вальне число редуктора і = 12; діаметр ролика І)_р = 0.4 м; статич­ний момент опору одного ролика М = 600 Н.м; момент інерції двигуна з редуктором / = 5 кг.м²;

прискорення і сповільнення рольгангу І а \ = 1.5 м/с².

30. Розрахувати, як буде змінюватись зусилля в канаті шахтної підіймальної установки (рис. 1.13), яка приводиться в рух асинхронним двигуном з фазним ротором потужністю Р_я = 500 кВт (л_н = 953 об/хв, = 2.2, / = 228 кг . м²), при розгоні з початковим пусковим моментом М_и = 1.8 Л/. Механічну харак­теристику вважати прямолінійною. Сумарний момент інерції обертових частин механізму, приведений до валу двигуна, /_мпр = 156 кг.м²; маса кліті з вантажем т_г = 15 .10³ кг; жорсткість одного метра канату с, = 1.8.10* Н .м; довжина канату / = 450 м; передавальне число редуктора і = 13; діаметр барабану Л. —

м.

Визначити також величину максимального зусилля в канаті, якщо пусковий момент залишатиметься постійним і рівним 1.8 М_н'

30. Скласти структурну схему й визначити всі її пара­метри для шахтної підіймальної установки (рис. 1.16), яка при­водиться в рух асинхронним двигуном з фазним ротором при розгоні з послідовно ввімкненими в колі ротора резисторами. Завантжена посудина знаходиться в нижньому положенні. Штуч­ну механічну характеристику асинхронного двигуна вважати пря­молінійною. Жорсткість одного метра підіймального канату с. = 2.2 .10⁸ Н.м. Момент інерції двигуна ^ = 3.1 кг.м²; усталена швидкість підіймання посудини г_м = 4.5 м/с відповідає номі­нальній швидкості обертання двигуна п_к = 570 об/хв; середнє прискорення посудини а_к = 3.1 м/с².

31. Робочий механізм з’єднаний з редуктором за допо­могою довгого валу, який має жорсткість с = ЗЛО⁵ Н.м/рад. Коефіцієнт в’язкого тертя передачі с_р = 2 .10³ Н . м с/рад; момент інерції механізму 7_м = 420 кг.м²; момент інерції двигуна з редуктором ^ = 1.2 кг .м²; передавальне число приводу і = 20; ККД передач г| = 0.9. Момент статичного навантаження меха­нізму М_и = 2700 Н .м; момент, який розвиває двигун під час розгону, вважати постійним і рівним М = 350 Н .м.

Визначити закон зміни моменту, що передається через гнучкий, вал та порівняти максимальні значення моментів з врахуванням і без в’язкого тертя.

Розв’язок

Середнє кутове прискорення валу

350 20 - 2700/0.9 ^

У, і² + /_м ' ^р 1.2 • 20 + 420

Частота коливань моменту при відсутності в'язкого тертя

^С{2 • (л • *Р + «^м)/(Л * ^гр ^м) ;

Q = ^3 • 10⁵ • (і.2 • 20² + 42о)Ді.2 • 20² • 42о) = 36.6 1/с .

Коефіцієнт заникання

а = Ріг • П²/2 • с₁₂ ; а = 2 ■ 10³ • 36.6²/2 ■ 3 • 10⁵=4.47 1/с . Частота коливань моменту при наявності в’язкого тертя Q₀ = Jn² - а² ; Q₀ = ч/зб.б² - 4.47² = 36.5 1/с •

Закон зміни моменту, що передається через гнучкий вал

м_в = м_и +/_м -е_сер ~/_м -є_сер-е-‘ • ((а • sin П₀/) / Q₀ + cosO₀/);

Л/_в = 2700 + 420 • 4.4 - 420 ■ 4.4 • е^АЛ1‘ • (X); де: (X) = ((4.47 • sin Зб.5ґ) / 36.5 + cos 36.5/).

Максимальне значення моменту при відсутності в’язкого тертя

М_в0 = 2700 + 420 • 4.4 + 420 - 4.4 = 6396 Н • м .

Максимальне значений Моменту при наявності в’язкого тертя буде, якщо Q₀t = тт, тобто при t = л/36.5 = 0.086 с.

М_{ъ ш} = 2700 + 420 • 4.4 + 420 • 4.4 • е~⁰'³⁸⁴ = 5812 Н • м

Співвідношення моментів к_и = М_ъ JЛґ_р0

к_и = 5812/6396 = 0.909 .

Максимальне значення моменту при наявності в’язкого тертя зменшиться на 91 %.

42. На рис. 1.22 зображена кінематична схема механізму

підіймання екскаватора ЕКГ 36/65А. Основні параметри меха­нізму: момент інерції барабанів з муфтами й гальмівними шкі­вами X = 300 ,10⁴ кг.м²; вага ковша з вантажем G_r = 130 т; вага

О к

Рис. 1.22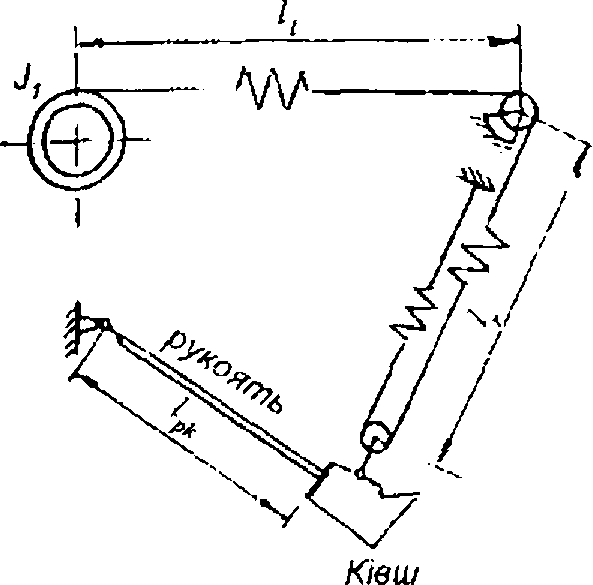

рукояті G = 22.8 т; кратність поліспаста к_л = 2; КІД механізму _л = 0.92; номі­нальна швидкість підіймання ковша v,

К

= 1.6 м/с; діаметр барабанів D₆ = 2.4 м ; діаметр канатів с/_к = 60 мм; модуль пружності канату Е_К = 1.05 ,10⁶ кг/см²; довжина канату /₂ = 92 м; довжина

канату /, змінюється. Номінальна шви-

•> і

дкість обертання двигуна n_v = 26 об/хв; момент інерції двигуна J = 300 кг. м². Привести що систему підіймаль­ного механізму до двомасової моделі та визначити її коефіцієнти й параметри.

• * *