- •Методические указания
- •Оглавление
- •Введение
- •1. Равномерное распределение
- •2. Экспоненциальное распределение
- •3. Распределение Эрланга -го порядка
- •4. Гамма-распределение
- •5. Распределение Вейбулла
- •6. Нормальное распределение
- •7. Логнормальное распределение
- •8. Бета-распределение
- •9. Распределение Пирсона типа V
- •10. Распределение Пирсона типа VI
- •12. Связанное распределение Джонсона
- •13. Несвязанное распределение Джонсона
- •14. Треугольное распределение
9. Распределение Пирсона типа V
Как уже отмечалось,
тогда и только тогда
![]() ,
когда
,
когда![]() .
Таким образом, мы получаем следующий
алгоритм, основанный на специальном
свойстве этого распределения.
.
Таким образом, мы получаем следующий
алгоритм, основанный на специальном
свойстве этого распределения.
1.Генерируем
![]() .
.
2. Возвращаем
![]() .
.
Можно использовать
любой метод для генерирования случайных
величин с гамма - распределением, только
необходимо учитывать, будет ли
![]() или
.
Применяя метод обратного преобразования
следует иметь в виду, что функция
распределения
или
.
Применяя метод обратного преобразования
следует иметь в виду, что функция
распределения
![]() есть функция
есть функция
![]() — функция распределения
— функция распределения
![]() .
Установив, что
.
Установив, что
![]() ,
получаем
,
получаем
![]() ,
как в буквальном методе обратного
преобразования, или
,
если
,
как в буквальном методе обратного
преобразования, или
,
если
![]() и
имеют
одно и то же распределение U(0,1).
В любом случае нам обычно следует
применять численный метод для оценки
и
имеют
одно и то же распределение U(0,1).
В любом случае нам обычно следует
применять численный метод для оценки
![]() .
.
Распределение
Пирсона типа V РТ5( |
|
Варианты распределений
|
Время выполнения какой-либо задачи (график функции плотности принимает форму, подобно графика плотности логарифмического распределения, но может иметь большой острый «выступ» ближе к x=0). |
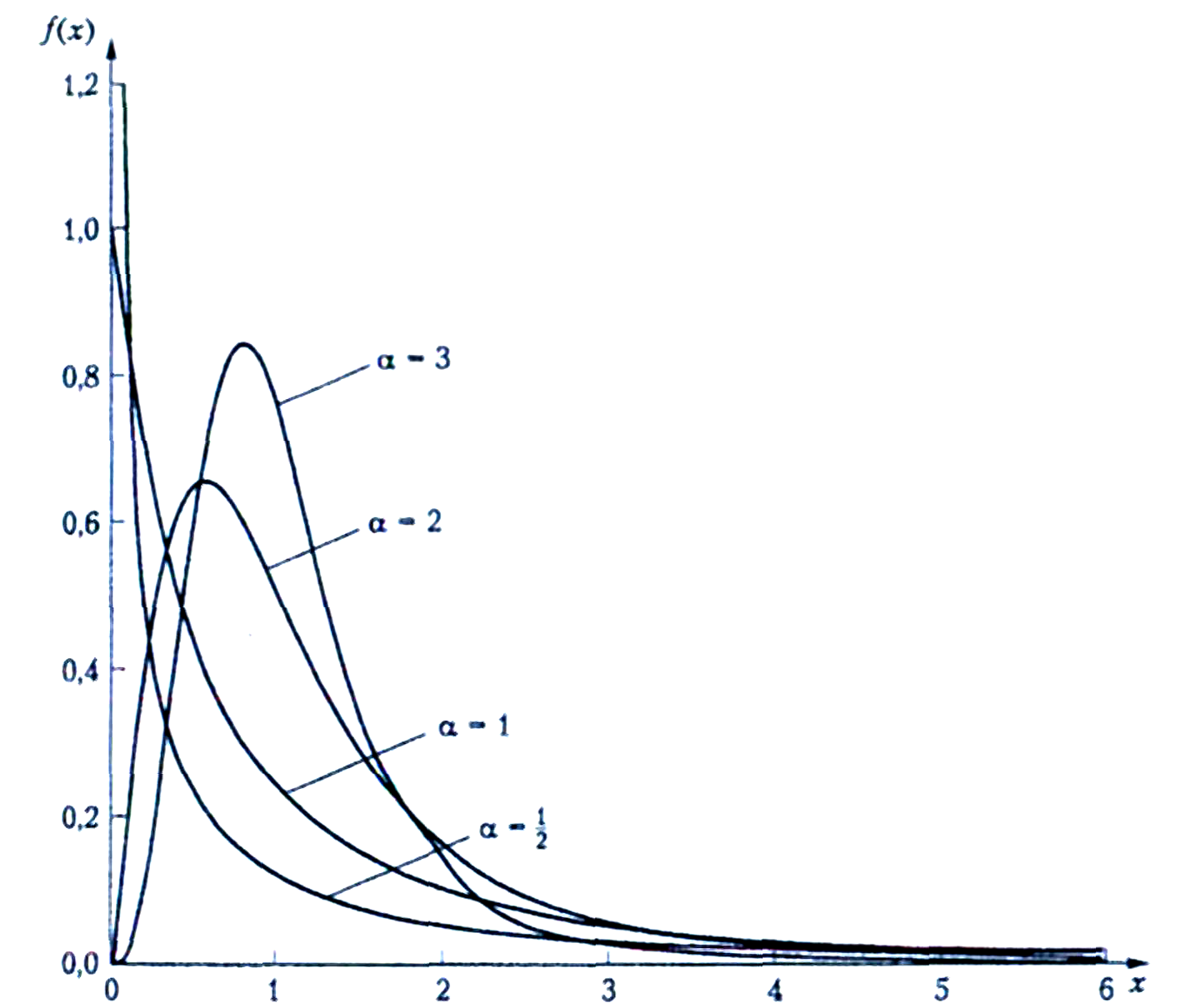
Плотность (рис.1.7.) |
|
Распределение |
где
|
Параметры |
Параметр формы , масштабный параметр |
Область |
|
Среднее |
|
Дисперсия |
|
Мода |
|
Оценка максимального правдоподобия |
При наличии
длинны
|
Примечания |
1. Тогда и только
тогда
2.Заметьте, среднее и дисперсия существуют только для определенных значений параметра формы. |
Рис. 1.7. Функции
плотностей распределения вероятностей
РТ5(
|
|
10. Распределение Пирсона типа VI
![]() ,
,
если
![]() а
а
![]() являются
независимыми величинами. Таким образом,
получаем следующий алгоритм.
являются
независимыми величинами. Таким образом,
получаем следующий алгоритм.
1. Независимо
генерируем![]()
2. Возвращаем
![]() .
.
Можно применять
любой метод для генерирования случайных
величин с гамма-распределением, необходимо
лишь проверить, будет ли
![]() .
При использовании метода обратного
преобразования учтите, что функция
распределения
.
При использовании метода обратного
преобразования учтите, что функция
распределения
![]() равна
равна
![]() для
для
![]() ,
где
,
где
![]() - это функция распределения
.
- это функция распределения
.
Распределение
Пирсона типа VI PT6( |
|
Варианты распределений
|
Время выполнения какой-либо задачи
|
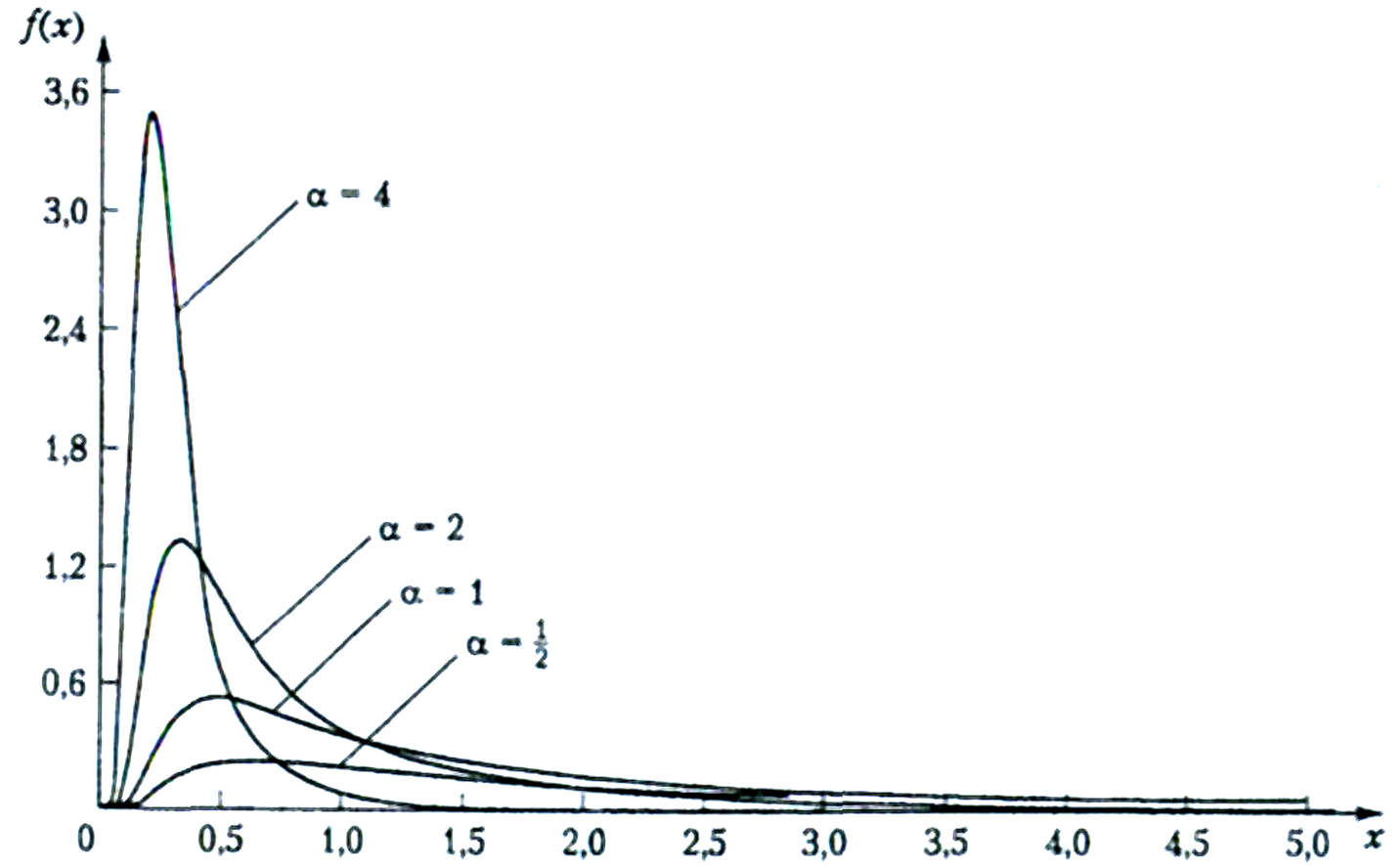
Плотность (рис.1.8.) |
|
Распределение |
где
|
Параметры |
Параметры формы и , масштабный параметр |
Область |
|
Среднее |
|
Дисперсия |
|
Мода |
|
Оценка максимального правдоподобия |
При наличии
данных
имеющих
распределение PT6(
к
|
Примечания |
1. Тогда и только
тогда X~ PT6(
),
когда
2.
Если
и
-
независимые случайные величины с
3.
Обратите внимание, что среднее и
дисперсия существуют только для
определенных значений параметра формы
|
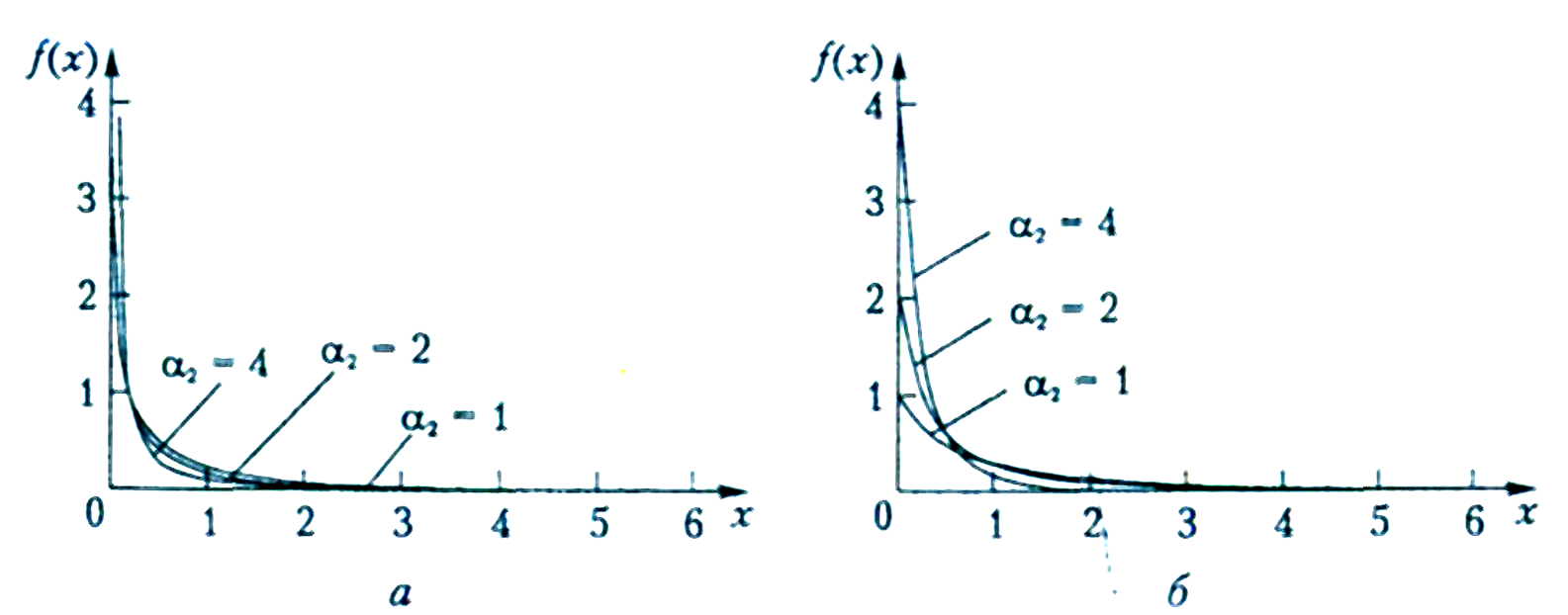
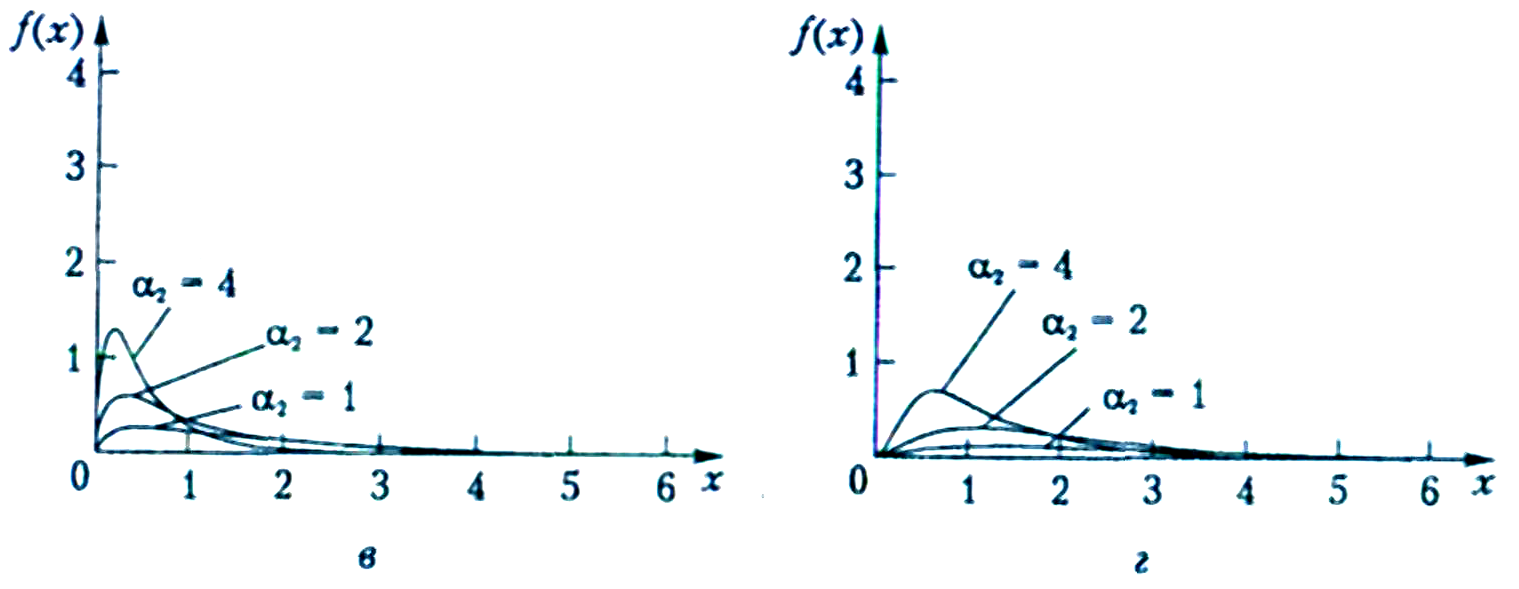
Рис.
1.8. Функции плотностей распределения
вероятностей PT6(
):
а -
Рис. 1.8. Функции
плотностей распределения вероятностей
PT6(
):
в-
г-
|
|
11. Лог-логистическое распределение
Функцию лог-логистического распределения можно обратить, чтобы получить
![]()
и в результате вывести алгоритм, используемый для обратного преобразования.
1. Генерируем .
2. Возвращаем
![]() .
.
Лог-логистическое
распределение
|
|
Варианты распределений |
Время выполнения какой-либо задачи |
Плотность (рис.1.9.) |
|
Распределение |
|
Параметры |
Параметр формы , масштабный параметр |
Область |
|
Среднее |
|
Дисперсия |
|
Мода |
|
Оценка максимального правдоподобия |
Допустим, что
Тогда
оценка максимального правдоподобия
для лог-логистического распределения
будут
Джонсон, Коц и Балакришнан предлагают решать уравнения (1) и (2) с помощью метода Ньютона. |
Примечания |
Тогда и только
тогда
|
Рис.1.9. Функции
плотностей распределения вероятностей
|
|



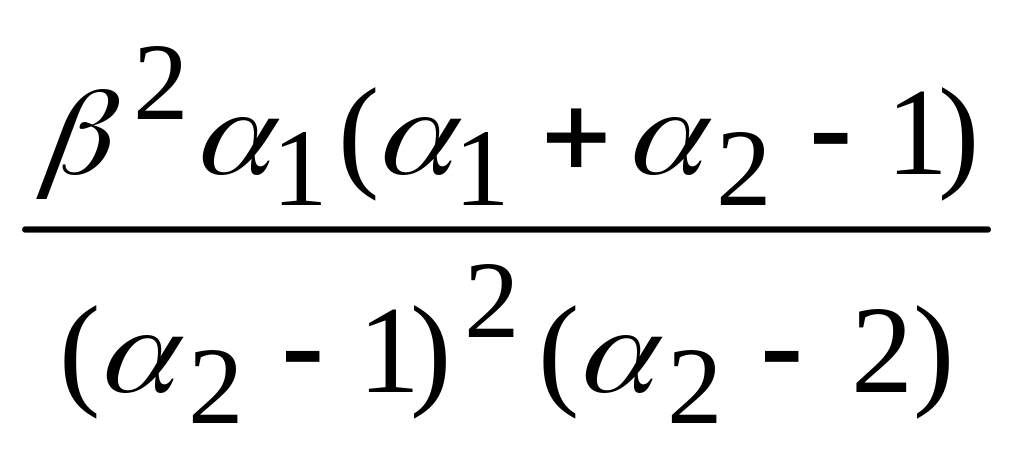 для
для
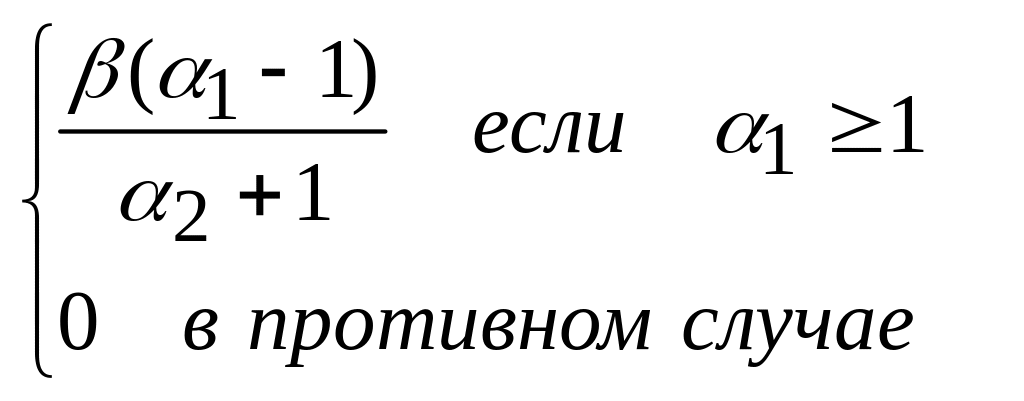
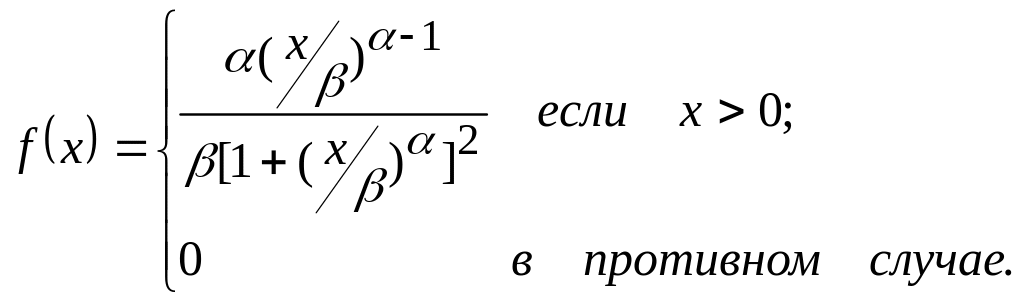
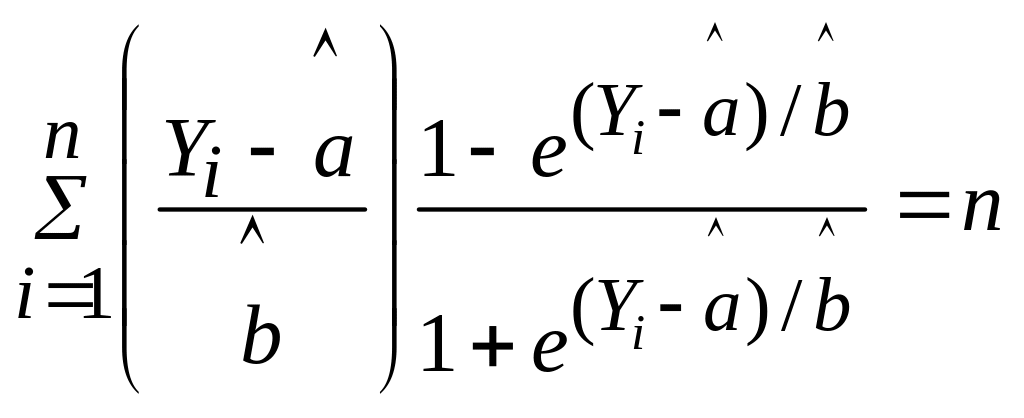 (2)
(2)