2. Экспоненциальное распределение

Рассмотрим алгоритм обратного преобразования экспоненциально распределенной случайной величины со средним :

1. Генерируем

2. Возвращаем

на шаге 2 равно , если мы хотим получить буквальную версию , чтобы добиться положительной корреляции между значениями и . Этот простой метод, обладающий всеми преимуществами метода обратного преобразования, работает достаточно быстро, большая часть времени идет на оценку логарифма.

Экспоненциальное распределение
Варианты распределений	Интервал времени между поступлениями требований в систему, происходящими с постоянной интенсивностью; время безотказной работы устройства.
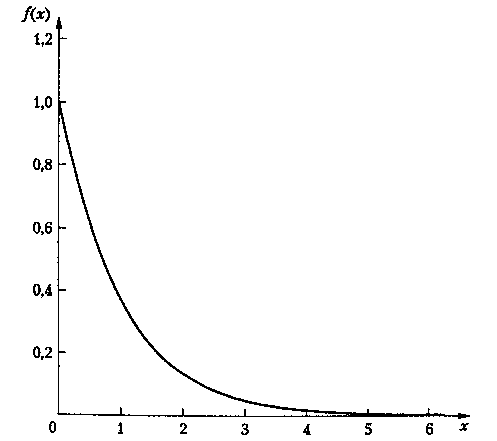
Плотность (рис.1.2.)
Распределение
Параметры	Масштабный параметр
Область
Среднее
Дисперсия
Мода	0
Оценка максимального правдоподобия
Примечания	1. Распределение -особый случай гамма-распределения и распределения Вейбулла (для масштабных параметров и в обоих случаях). 2. Если - независимые случайные величины с распределением , то , именуемое также распределением Эрланга m-го порядка. 3. Экспоненциальное распределение – это единственное непрерывное распределение с отсутствием последствия.
Рис.1.2. Функция плотности распределения вероятности

3. Распределение Эрланга -го порядка

Если X - случайная переменная с распределением Эрланга m-го порядка со средним , можно записать, что , где - независимые и одинаково экспоненциально распределенные случайные переменные со средним каждая. Так был получен алгоритм свертки, однако его эффективность можно улучшить следующим образом. Если мы воспользуемся методом обратного преобразования для генерирования экспоненциально распределенных величин , где - независимые и одинаково распределенные случайные величины с распределением U(0,1)], то получим

,

так что нам понадобится оценить только один логарифм (а не m логарифмов). Тогда формулировку этого алгоритма получим следующим образом.

1. Генерируем как независимые и одинаково распределенные величины с распределением U(0, 1).

2.Возвращаем .

(В данном случае снова нужно заранее вычислить и сохранить его для повторного использования.) Этот алгоритм действительно является комбинацией методов композиции и обратного преобразования.

4. Гамма-распределение

Случайные величины с гамма - распределением сложнее генерировать, нежели три типа случайных величин, поскольку функция распределения для них не имеет конечной формы, для которой мы могли бы попробовать найти обратную функцию. Во-первых, при заданном для любого можно получить случайную величину X', задав , так что достаточно ограничить рассмотрение генерированием величин из распределения . Во-вторых, вспомните, что распределение является экспоненциальным распределением со средним 1, то есть нам понадобится рассматривать только и Поскольку алгоритмы для генерирования случайных величин с гамма - распределением, как правило, действительны только в одной из этих областей значений , мы будем рассматривать их отдельно. В работе Тадикамаллы и Джонсона [Tadikamalla and Johnson, 1981] содержится всесторонний обзор методов генерирования величин с гамма -распределением, доступных на данный момент.

Сначала рассмотрим случай, когда 0< <1. (Заметьте, что, если = 0,5, мы имеем дело с распределением с измененным масштабом и что X можно просто генерировать, нижеприведенный алгоритм действителен и для ) Аткинсон и Пирс [Atkinson and Pearce, 1976] для этого случая проверили три альтернативных алгоритма (представляем один из них, опираясь на исследования Аренса и Дитера [Ahrens and Dieter, 1974]). Алгоритм Форсита [Forsythe, 1972] работает гораздо быстрее алгоритмов Аткинсона и Пирса [Atkinson and Pearce, 1976], но он гораздо сложнее. Рассматриваемый нами алгоритм, обозначенный в работе Аренса и Дитера [Ahrens and Dieter, 1974] как GS, представляет собой метод принятия-отклонения с оцениваемой сверху функцией

Таким образом, , где , в результате получаем

Случайную величину Y плотностью можно генерировать с помощью метода обратного преобразования; при этом функция распределения, соответствующая , будет иметь вид

Ее можно обратить, чтобы получить

Таким образом, чтобы генерировать с плотностью r, сначала генерируем . Если , устанавливаем ; тогда . В противном случае, если , устанавливаем , что будет больше 1.

Учитывая, что

получаем конечный алгоритм должно быть определено заранее).

1.Генерируем , и пусть . Если Р > 1, переходим к шагу 3. В противном случае переходим к шагу 2.

2.Допускаем , генерируем . Если , возвращаем Х= Y.

В противном случае возвращаемся к шагу 1.

3.Допускаем , генерируем . Если возвращаем X=Y. В противном случае возвращаемся к шагу 1.

Далее рассмотрим случай, когда , для которого существует несколько хороших алгоритмов. Принимая во внимание опыты с учетом времени Шмейсера и Лала [Schmeiser and Lai, 1980b], Чента и Фиста [Cheng and Feast, 1979], мы представляем модифицированный метод принятия-отклонения, встречающийся в работе Чеига [Cheng, 1977], автор называет его алгоритмом GB. Время выполнения этого алгоритма связано с , он работает быстрее по мере увеличения значения а. (Модификация метода принятия-отклонения заключается в добавлении более быстрой предварительной проверки на принятие.) Для того чтобы получить оцениваемую сверху функцию , сначала определим и . Затем определяем , где

Функция распределения, соответствующая плотности , составляет

Ее легко инвертировать, чтобы получить

Ченг [Cheng, 1977] в своей работе доказал, что - действительно оцениваемая сверху функция . Это пример получения оцениваемой сверху функции, когда сначала задается известное распределение (R(x) на самом деле является функцией лог-логистического распределения с параметром формы , масштабным параметром и параметром положения 0), а затем изменяется масштаб плотности , чтобы оценивать сверху функцию . Следовательно, мы используем метод обратного преобразования для генерирования величины Y с плотностью r. После добавления эффективного предварительного испытания на принятие и упрощение для вычислительной эффективности Ченг [Cheng, 1977] представил следующий алгоритм (предварительно определяемые константы составляют:

и

1. Генерируем и как независимые и одинаково распределенные случайные величины с распределением U(0, 1).

2.Допускаем

3. Если , возвращаем X=Y.В противном случае переходим к шагу 4.

4. Если , возвращаем X=Y. В противном случае переходим к шагу

Шаг 3 - это добавленная предварительная проверка, в случае прохождения которой можно избежать вычисления логарифма на шаге 4 обычного метода принятия-отклонения. (Если шаг 3 удалить, алгоритм все еще будет действительным, он просто превратится в метод принятия-отклонения.)

Гамма – распределение
Варианты распределений	Время выполнения какой – либо задачи, например обслуживания клиента или ремонта машины
Плотность (рис.1.3.)	где - гамма–функция, определяемая как для любого вещественного числа Свойства гамма – функции для любого для любого неотрицательного целого числа ; для любого положительного целого числа .
Распределение	Если не является целым числом, конечной формы не существует. Если - положительное целое число, тогда
Параметры	Параметр формы , масштабный параметр
Область
Среднее
Дисперсия
Мода
Оценка максимального правдоподобия	Должны выполняться два следующих равенства: которые могут быть решены численно. и называется дигамма – функцией. -производная от .) Альтернатива получения приближённых значений и . Пусть . Получаем как функцию T, пусть .
Примечания	1.Распределение и одинаковы. 2.Для положительного целого числа называется распределением Эрланга m-го порядка. 3.Распределение хи – квадрат с степенями свободы - это то же, что и 4.Если независимые случайные величины с , то 5.Если - независимые случайные величины с 6.Тогда и только тогда , когда имеет распределение Пирсона типа 5 с параметром формы и масштабным параметром , обозначаемое как РТ5 . 7.
Рис.1.3. Функция плотностей распределения вероятностей