Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Восточноукраинский национальный университет им. В. Даля

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1.1 Распределения.doc

Скачиваний:

Добавлен:

23.08.2019

Размер:

5.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

7. Логнормальное распределение

Специальное свойство логнормального распределения - если , то - используется, чтобы получить следующий алгоритм.

1. Генерируем .

2. Возвращаем .

Для выполнения шага 1 можно взять любой из методов генерирования нормально распределенных случайных величин.

Помните о том, что и не являются средним и дисперсией распределения . В действительности, если , и мы определяем , то получается, что . Следовательно, если мы намерены генерировать логнормально распределенную случайную величину X с заданным средним и заданной дисперсией , необходимо сначала определить и в исчислении и , перед тем как генерировать промежуточную нормально распределенную случайную величину Y. Получаем следующие формулы:

;

Логнормальное распределение
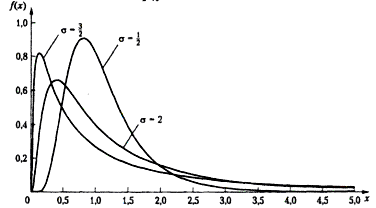
Варианты распределений	Время выполнения какой-либо задачи (график функции плотности принимает форму, как у графиков плотности gamma и распределений Weibull для >1, но может иметь большой острый «выступ» ближе к x=0, что бывает полезно); величины, являющиеся произведением большого числа других величин (на основании центральной предельной теоремы)
Плотность (рис.1.6.)
Распределение	Конечная форма отсутствует
Параметры	Параметр формы , масштабный параметр
Область
Среднее
Дисперсия
Мода
Оценка максимального правдоподобия
Примечания	1. Тогда и только тогда , когда . Поэтому, если считается, что данные имеют логнормальное распределение, логарифмы точек данных могут рассматриваться как нормально распределенные данные для построения гипотез относительно распределения, оценки параметров и проверки по критерию согласия. 2. При логнормальное распределение становится вырожденным в точке . Плотности логнормальное распределения для небольших значений имеют резкое возрастание в моде. 3. независимо от значений параметров
Рис.1.5. Функции плотности распределения вероятностей

8. Бета-распределение

Вначале обратите внимание, что мы можем получить в интервале [а,b] для а<b, установив , где в интервале [0,1]. Так что достаточно рассмотреть последний случай, который мы дальше будем называть распределением .

Некоторые свойства распределения для определенных комбинаций обеспечивают генерирование случайных величин с бета-распределением. Во-первых, если , то , так что мы можем без труда генерировать случайную величину с распределением , если удается легко получить случайную величину с распределением . Такая ситуация возникает, когда или , или равно 1. Если -1, мы получаем для , так что функция распределения , и мы можем без труда генерировать с помощью метода обратного преобразования, то есть возвратив для . Наконец, распределение beta(l,1) - это распределение U(0,1).

Общий метод генерирования случайных величин с распределением для любых значений и основывается на том факте, что если , а , и являются независимыми величинами, то . Таким образом, мы получаем следующий алгоритм:

1. Независимо генерируем .

2. Возвращаем .

Две случайные величины и с гамма - распределением можно генерировать по соответствующему алгоритму генерирования случайных величин с гамма-распределением, так что нам нужно проверить, когда и , будут меньше или больше 1.

Этот метод достаточно удобен, поскольку он, по сути, выполняется для всех значений при условии, что у нас есть генераторы случайных величин с распределением . Эффективность его выполнения зависит от скорости работы выбранных генераторов случайных величин с гамма-распределением.

Бета-распределение
Варианты распределений	Используется как приблизительная модель при отсутствии данных (см.раздел 6.11); распределение случайной доли (доли бракованных товаров в партии); время выполнения задачи, скажем, в сетевом графике
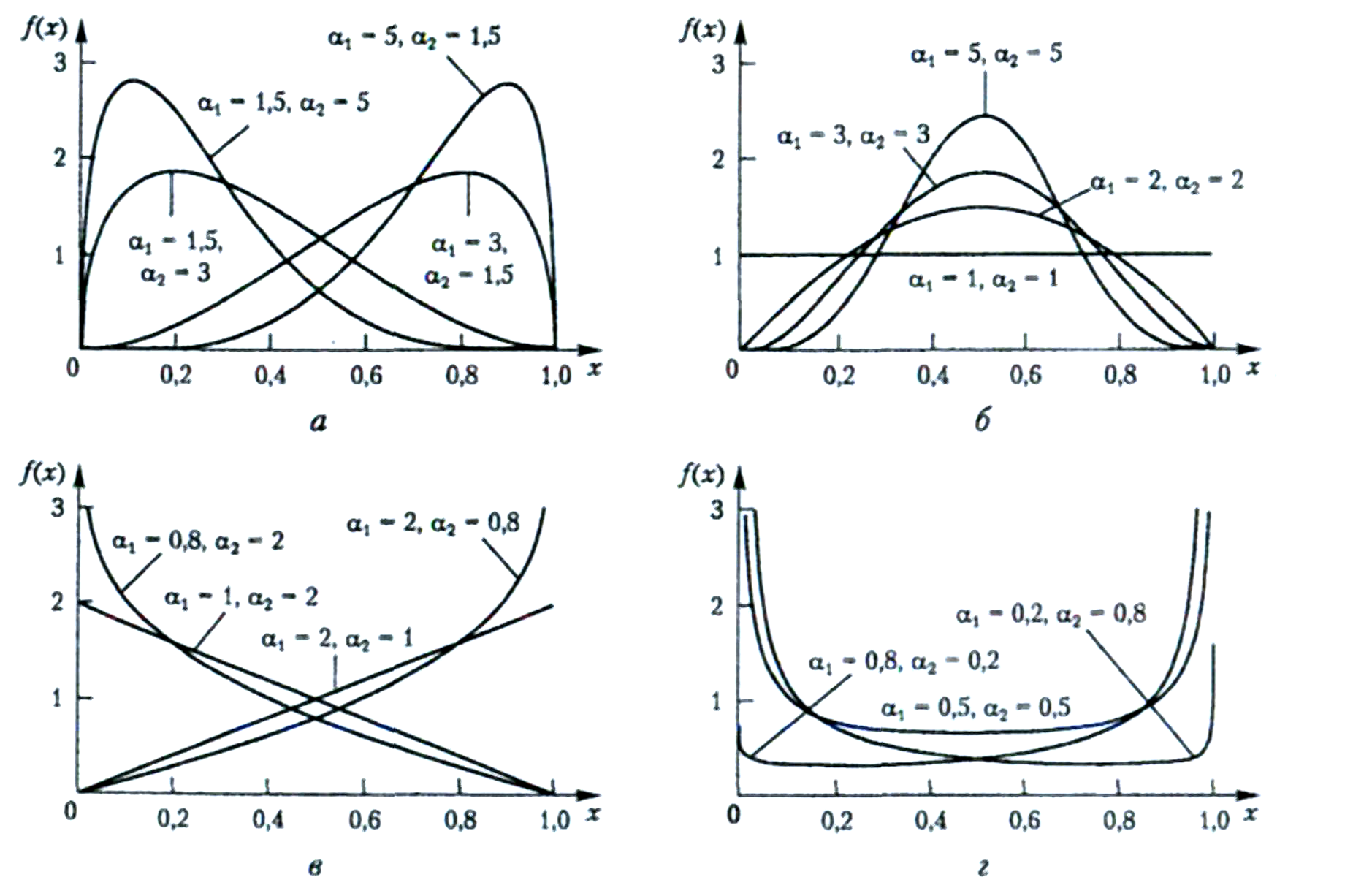
Плотность (рис.1.6.)	где -бета-функция, определяемая как для любых вещественных чисел . Некоторые свойства бета-функции:
Распределение	В целом конечная форма отсутствует. Если или является положительно целым числом, можно воспользоваться биномиальным разложением, чтобы получить , которая будет многочленом в точке х, как правило, будут положительными вещественными числами от 0 до
Параметры	Параметры формы и
Область
Среднее
Дисперсия
Мода
Оценка максимального правдоподобия	Должны выполняться два следующих равенства: где -дигамма-функция; и ; заметьте, что . Найти оценку максимального правдоподобия решив эти уравнения.
Примечания	1. Распределение U(0,1) и beta(1,1) одинаковы. 2. Если и - независимые случайные величины с , то . 3. Для случайной величины Х с бета-распределением в интервале [0,1] можно изменить масштаб и размещение, чтобы получить случайную величину Х с бета-распределением в интервале [a, b] с той же формой путем трансформации . 4. Тогда и только тогда , когда . 5. Тогда и только тогда , когда имеет распределение Пирсона типа VI с теми же параметрами формы и масштабным параметром 1, обозначаемое как РТ6 ( ,1). 6. Плотность beta(1,2) – левый треугольник, а плотность beta(2,1) – правый треугольник. 7. 8. Тогда и только тогда плотность симметрична , когда . Среднее и мода равны тогда и только тогда, когда .
Рис.1.6. Функции плотностей распределения вероятностей а-г при различных значениях и