20. Могут ли формулы и быть формулами одной и той же квадратичной формы в разных базисах?
Решение. (не ручаюсь, что так надо решать, надо спросить у преподавателя).
Инвариантами квадратичной формы являются индексы инерции (т.е. они одинаковые для различных базисов). Индекс положительной инерции равен числу положительных собственных значений матрицы квадратичной формы, а индекс отрицательной инерции - числу отрицательных собственных значений матрицы квадратичной формы (вне зависимости от базиса).
1) Находим собственные
значения для
.
Матрица
квадратичной формы:
.
Решаем характеристическое уравнение: или
или
.
Следовательно,
- индексы положительной и отрицательной
инерции.
2) Находим собственные
значения для
.
Матрица
квадратичной формы:
.
Решаем характеристическое уравнение: или
или
.
Следовательно, - индексы положительной и отрицательной инерции.
Вывод: т.к. индексы в 1-м и 2-м случае совпали, то в принципе формулы и быть формулами одной и той же квадратичной формы в разных базисах
21. Запишите
матрицу билинейной формы
где
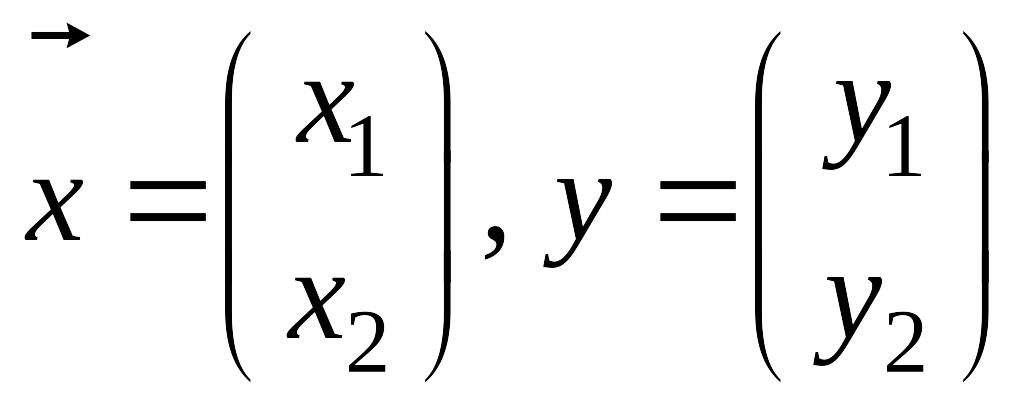- векторы
из R2,
(а)
в стандартном базисе, (b)
в базисе, состоящем из векторов
.
Постройте соответствующую квадратичную
форму и запишите ее матрицу в тех же
базисах. Является ли получившаяся
квадратичная форма положительно или
отрицательно определенной?
Решение. Используя определение скалярного произведения запишем данную форму в виде:
.
Матрица
билинейной формы
в базисе
определяется по формулам:
.
1)
В стандартном
базисе
.
В нашем
случае рассчитываем
;
;
;
.
Матрица билинейной
формы::
.
Квадратичная
форма:
.
Матрица квадратичной
формы в базисе {e}:
.
2) В базисе . В нашем случае рассчитываем
;
;
;
.
Матрица билинейной
формы:
.
Билинейная форма
в базисе
:
.
Квадратичная
форма в базисе
:
.
Матрица квадратичной
формы в базисе
:
.
3) Проверяем квадратичную форму на положительно или отрицательно определенность по критерию Сильвестра. Главные миноры матрицы равны:
.
Следовательно, т.к. не все главные миноры положительные (и не все отрицательные), то это означает, что квадратичная форма не является положительно определенной (и не является отрицательно определенной).
Действительно, в
стандартном базисе
.
Но для ненулевого вектора
видим, что
квадратичная форма не положительная.
22. Найдите ортонормированный базис, в котором квадратичная форма имеет канонический вид.
Решение. Найдем ортонормированный базис из собственных векторов матрицы квадратичной формы.
1)
Матрица квадратичной формы
:
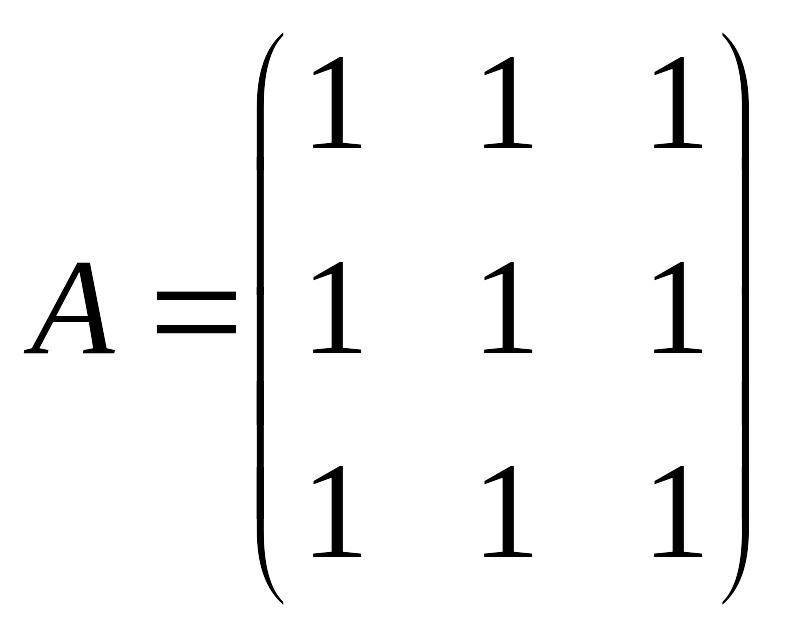
2) Решаем характеристическое уравнение 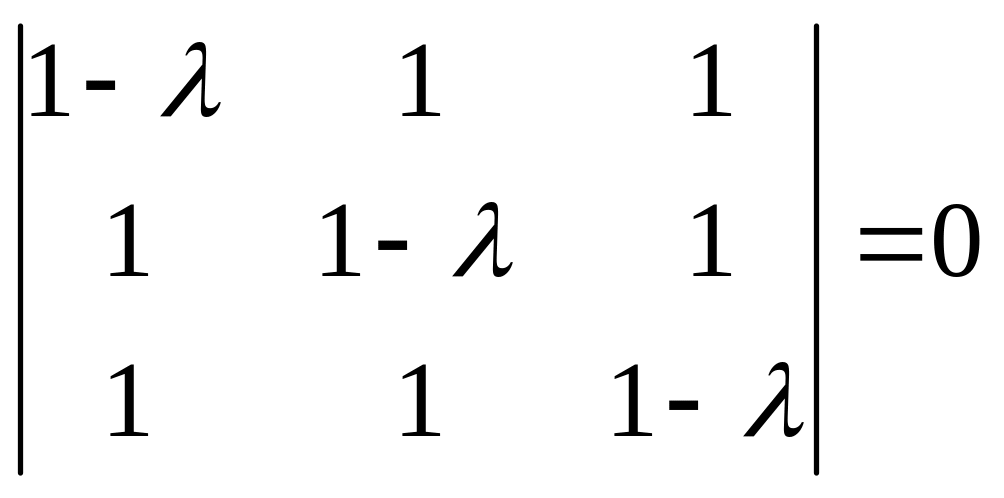или
или
.
Следовательно,
- собственные значения.
3) Находим собственные вектора, решая систему .
а)
.
Решаем систему
.
Здесь - базисная переменная, а - небазисные переменные.
Полагая
,
получаем собственный вектор
.
Полагая , получаем собственный вектор .
Произведем ортогонализацию полученных собственных векторов.
,
.
Проведем проверку
(необязательно):
.
Итак, найдены
ортогональные собственные вектора
и
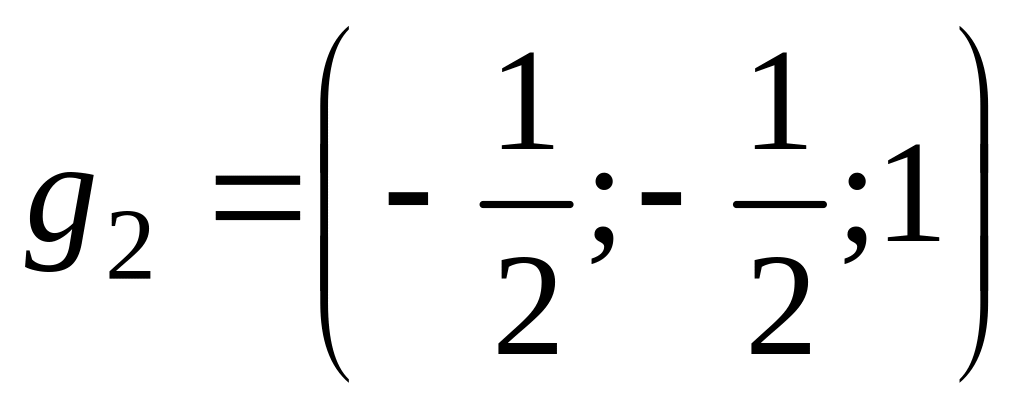отвечающие
.
б)
.
Решаем систему
.
Здесь - базисные переменные, а - небазисная переменная.
Полагая
,
получаем собственный вектор
для
.
4) Т.к. матрица оператора, заданного в ортонормированном базисе, является симметричной, то это означает, во-первых, что оператор является самодвойственным, а во-вторых, собственные вектора отвечающие разным собственным значениям ортогональны.
Следовательно, , , - ортогональный базис из собственных векторов оператора.
Произведем нормировку (сделаем вектора единичными):
,
,
.
Итак,
-
ортонормированный базис из собственных
векторов оператора
5) Заменой (ставим в столбцы координаты ):
или
.
Отметим, что
матрица C
– ортогональная, поэтому для нахождения
обратной достаточно ее транспонировать
(
),
т.е.
- обратное преобразование.
В ортонормированном базисе квадратичная форма имеет канонический вид:
.