13. Основные свойства задач линейного программирования. (Первая геометрическая интерпретация. Основная теорема линейного программирования.)

Общая задача линейного программирования:

Дана целевая функция f(x)= C₁x₁+C₂x₂+…+C_nx_n. Найти f(x*)→min f(x) на множестве Х, заданном ограничениями вида.

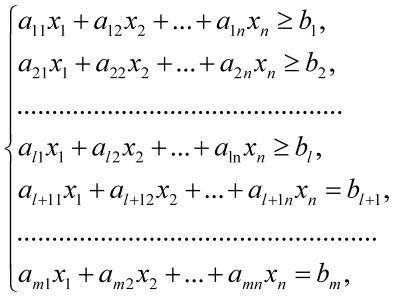
x_s1 >= 0 , x_s2 >= 0, …, x_sk >= 0, (1<= k <= n)

Допустимое множество Х общей ЗЛП образует многогранное множество. Если это множество ограничено, его называют многогранником.

Множество M называется выпуклым, если любые его две точки можно соединить отрезком прямой целиком принадлежащей множеству M.

Точка Х^о выпуклого многогранного множества М называется его угловой точкой, если она не лежит ни на каком отрезке, соединяющем какие – либо две точки множества М, отличные от нее.

Угловые точки многогранника называются его вершинами.

Основная теорема ЛП: пусть {x*}-множества всех решений задачи ЛП. Тогда {x*} содержит хотя бы одну угловую точку.

Это хорошо иллюстрируется при геометрическом методе решения – линейной интерпретации ЗЛП.

Геометрический метод решения:

на координатных осях строятся полуплоскости ограничений, получается ОДЗ целевой функции

строится прямая – вектор f(x)

если f(x)→min, то двигаем вектор параллельным переносом вниз до границ ОДЗ (если f(x)→mах, то вверх)

далее возможны 3 случая:

задача имеет единственное решение – вектор целевой функции проходит через одну вершину ОДЗ

Задача имеет бесконечное множество решений – вектор целевой функции совпадает с одной из граней допустимого множества.

задача не имеет решений – допустимое множество представляет собой неопределенное многогранное множество (не ограничено снизу, неограниченно убывает).

Геометрическое представление ЗЛП с двумя переменными называется первой геометрический интерпретацией.

14. Модели линейного программирования (простейшая задача производственного планирования). Задача.

Разработка модели ЛП включает следующие основные:

1. определение переменных задачи.

2. представление ее ограничений в виде линейных уравнений или неравенств.

3. задачи линейной целевой функции, подлежащей минимизации или максимизации.

Классической формой модели ЛП является простейшая задача производственного планирования.

Постановка задачи: пусть имеется некоторый экономический объект, который может производить n видов продукции. В процессе производства допустимо использование m видов ресурсов. Применяемые технологии характеризуются затратами единиц сырья на единицу продукции.

Обозначим через a_ij количество i-го ресурса, который тратится на производство единицы j-го вида продукции.

Если j-й продукт производится в количестве х_j, то нужно потратить а_1jх_j первого ресурса, а_2j,x_j второго и так далее.

Свободный план производства по всем видам продукции может быть представлен в виде n-мерного вектора строки х=(х₁, х₂,…, х_j… х_n).

Тогда общие затраты i-го ресурса на производство всех продуктов: ∑ⁿ_j=1 a_ij*x_j.

Вводится ограничения на используемые ресурсы b=(b_1,b₂,…b_m), где b_i – максимальное количество i-го ресурса: a_m1x₁+a_m2x₂+…a_mnx_n≤b_m.

Ограничения по производственным мощностям: х_i≤b_i. Естественные ограничения на не отрицательность компонентов плана производства х₁≥0, х₂≥0,…х_n≥0.

Обозначив через С_j цену единицы j-го продукта, получим выражение суммарного дохода от выполнения плана производства, задаваемого вектором х: f(х)= C₁x₁+C₂x₂+…+C_nx_n тогда задача: f(x)→mах, х € Х. Если С_j –общие расходы на производство j-го продукта, то f(x)→min, х € Х.

Задача нелинейного программирования является частным случаем задачи математического программирования.

В общем виде задача МП формулируется следующим образом: дана целевая функция f(x); допустимое множество х задано ограничениями вида: q_i(x)≤0, i=1,m; q_i(x)=0, i=m+1, m+l

Множество Х является частью пространства Rⁿ.

Нелинейного программирования выглядит следующим образом: f(x)→min, х € Х;

Х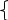 : q_i(x)≥0, i=1,l

h_i(x)=0, i=l+1,m

классическая задача на условный экстремум функции многих переменных есть задача МП, в которой допустимо множество х задается только уравнениями: f(x)→min, х € Х; Х={x| x € Rⁿ , h_i(x)=0, i=1,m }.

Решается задача методом множителей Лагранжа: L_y(x)= f(x) +∑^m_i-1 y_i h_i(x) –функция Лагранжа, у – множитель Лагранжа.

Пусть f(x), h₁(x)… h_m(x) непрерывно дифференцируемы в окрестностях х* € Х. Тогда, если х* - локальное решение задачи МП, то существует такой набор значений у*=(у₁*…,у_n*), что ∂Ly*(x*)/∂x_i=0, i=1,n (*) при у=у* и условии, что ∆ h_i(x*) линейно независим.

Условие линейной независимости градиентов называется условием регулярности задачи МП. Любая точка х*, удовлетворяющая условию (*) называется стационарной точкой задачи МП.

В соответствии с методом множителей Лагранжа задачи МП преобразуется к виду: Ly(x) →min, x € Rⁿ.

Алгоритм преоразования:

1. находим ∂Ly(x)/∂x_i=0, i=1,n. Решение: х^о=(х₁^о(у),…,х^о_n (у))

2. подставляем х^о в Х={x| x € Rⁿ , h_i(x)=0} и решаем полученную систему алгебраическим уравнением относительно у.

Если рассматривать функцию Ly(x) как функцию всех переменных ∆(х₁,…х_n,…у₁…,у_m), то точка х*( х*₁ ,…х*_n,…у*₁…,у*_m) не является точкой экстремума. Она является седловой точкой задачи МП.