Моменты. Дисперсия. Среднее квадратическое отклонение.

Кроме МО, в теории вероятностей используется еще ряд ЧХ различного назначения. Среди них основную роль играют моменты – начальные и центральные.

Определение. Начальным моментом -го порядка СВ называется МО -ой степени этой СВ:

, (2.9)

если МО существует.

Как правило, используют начальные моменты целого положительного порядка. В частности, при имеем , а при .

Определение. Центральным моментом -го порядка СВ называется МО -ой степени отклонения этой СВ от ее МО:

, (2.10)

если МО существует.

СВ называется центрированной СВ (так как ). Таким образом, центральный момент – это начальный момент для центрированной СВ:

.

Аналогично начальным моментам, центральные моменты обычно используют целого положительного порядка.

В частности, при имеем для всех СВ.

Особое значение для практики имеет второй центральный момент , который называется дисперсией СВ и обозначается .

Определение. Дисперсией СВ называется МО квадрата отклонения СВ от ее МО:

. (2.11)

Для дисперсии справедливо также следующее выражение:

Таким образом, наряду с (2.11)

. (2.12)

С помощью формулы (2.12) на практике вычислять дисперсию часто бывает проще.

Дисперсия характеризует степень разброса (рассеивания) значений СВ относительно ее среднего значения (МО). Чем плотнее группируются значения СВ около МО, тем дисперсия меньше (ср. со смыслом параметра в нормальном законе распределения).

Механическая интерпретация дисперсии. Дисперсия представляет собой момент инерции распределения масс относительно центра масс (центра тяжести, МО).

Вычисляются начальные моменты по формулам, вытекающим из ОТМО для функции :

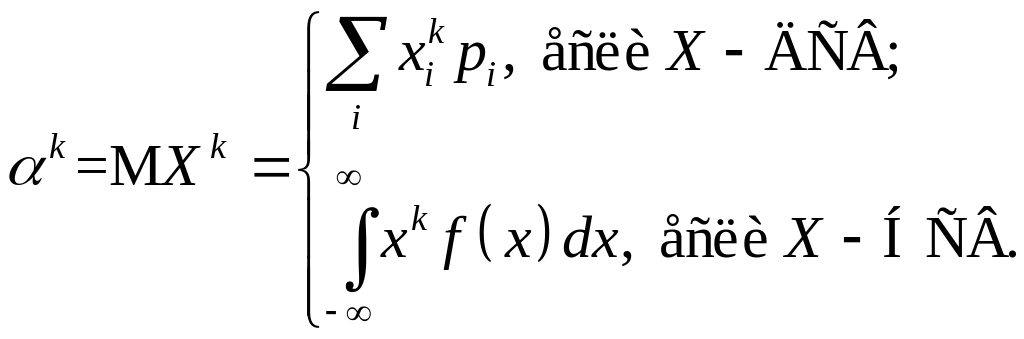
Центральные моменты вычисляются по формулам, вытекающим из ОТМО для функции :

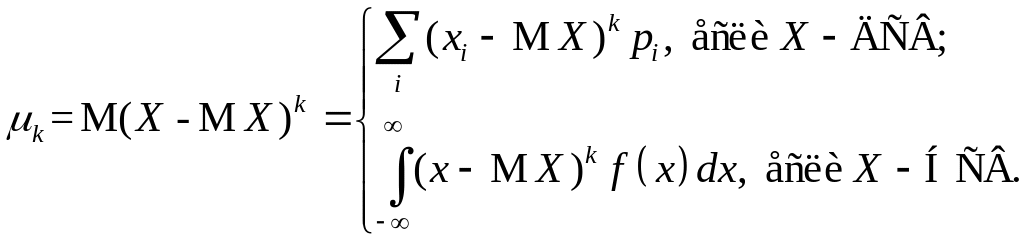
Формулы для вычисления дисперсии вытекают из ОТМО для функции (если используется формула (2.11)) или функции (если используется формула (2.12)):

Свойства дисперсии

1. , тогда и только тогда, когда .

▲ Свойство следует из свойства 4 МО ■.

2. Дисперсия не изменяется при прибавлении к СВ константы:

.

▲ ■.

3. Константа из-под знака дисперсии выносится с квадратом:

.

▲ ■.

Дисперсия имеет размерность квадрата СВ. Характеристикой рассеивания, размерность которой совпадает с размерностью СВ, является среднее квадратическое отклонение (стандартное отклонение), определяемое как корень арифметический из дисперсии:

.

С учетом данного определения часто пишут: .

Другие используемые на практике ЧХ.

Величина , определяемая равенством , называется - квантилем распределения СВ .

Квантиль называется медианой распределения СВ . Другими словами, медиана – это значение на числовой прямой, для которого

Модой распределения НСВ называется число , при котором ПВ достигает максимального значения. Распределения с одной модой называются унимодальными, а распределения с несколькими модами – мультимодальными.

Для симметричных распределений медиана, мода и МО совпадают.