Самарский государственный аэрокосмический
университет имени академика С.П. Королева
Кафедра «Техническая кибернетика»
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Курс лекций
для студентов, обучающихся по направлению
010400 Информационные технологии
Часть 2
Случайные величины
Лектор: к.ф.-м.н., доцент
Коломиец Э.И.
САМАРА 2012
Случайные величины. Функция распределения случайной величины и ее свойства
Интуитивное представление о случайной величине.
Случайная величина (СВ) – это числовая функция, значения которой заранее (до наблюдения) нельзя точно определить, то есть функция, зависящая от случайного исхода и принимающая свои значения с некоторыми вероятностями.
Примеры СВ:
а) число пассажиров в автобусе (конечное число значений);
б) число вызовов на телефонной станции за время Т (счетное число значений);
в) время безотказной работы прибора за время Т (несчетное число значений).
Обозначают СВ прописными буквами латинского алфавита X, Y, Z,…, а их значения соответствующими строчными буквами x, y, z,….
Формальное определение СВ.
Определение.
Случайной
величиной
называется
функция X
= X(ω),
определенная на пространстве элементарных
событий
и принимающая действительные значения
(
).
Для того, чтобы определять вероятности событий, связанных со СВ, и делать это одним и тем же способом для любых СВ, в теории вероятностей вводится понятие функции распределения.
Определение.
Функцией
распределения
СВ
называется функция
действительной переменной
,
определяемая при каждом
равенством:
.
Геометрически функция распределения (ФР) означает вероятность попадания СВ левее заданной точки :
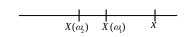
ФР является исчерпывающей вероятностной характеристикой СВ. Это вытекает из следующих ее свойств.
Свойства ФР.
1.
для любого
(свойство очевидно,
так как
- вероятность).
2. ФР является
функцией неубывающей:
.
▲
.
Поэтому в силу свойства 6 вероятности
■.
3.
.
▲
в силу свойства 5
вероятности.
в силу аксиомы
нормированности ■.
4. ФР является функцией непрерывной слева, то есть для любого
,
где
- предел слева ФР в точке х.
5. Для любого
,
где
- предел справа ФР в точке х.
Замечание.
Геометрически свойства 4 и 5 означают
следующее. В точках
,
где ФР имеет разрыв 1 рода, то есть когда
,
значением ФР является левое (нижнее,
меньшее). В точках непрерывности ФР
свойства 4 и 5 содержательными не являются.
6. Вероятность
попадания СВ
в интервал
определяется как приращение ФР на этом
интервале: для любых
.
▲ Поскольку событие
и слагаемые в сумме являются несовместными,
то в силу аддитивности вероятности
или, что эквивалентно,
■.
7. Для любого
,
где
- величина скачка ФР в точке
.
▲ Поскольку событие
и слагаемые в сумме являются несовместными,
то в силу аддитивности вероятности
,
а с учетом свойства 5 ФР
■.
Следствие.
Если ФР непрерывна в точке
,
то
.
Если ФР непрерывна для любого
,
то
для любого
.
8.
.
9.
.
10.
.
(Доказать свойства 8, 9 и 10 самостоятельно).
В общем случае график ФР может иметь вид:
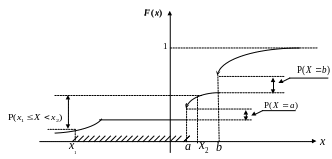
В приложениях, как правило, встречаются СВ, ФР которых являются либо везде кусочно-постоянными (дискретные СВ), либо везде непрерывными и даже гладкими (непрерывные СВ). В каждом из этих случаев существуют более удобные, чем ФР, вероятностные характеристики СВ.