Числовые характеристики случайных величин

ФР, ЗР и ПВ полностью характеризуют ДСВ и НСВ с вероятностной точки зрения. Однако во многих практических задачах нет надобности в таком полном описании СВ. Часто бывает достаточно указать только отдельные числовые параметры, характеризующие существенные черты распределения вероятностей СВ. Числа, выражающие в сжатой форме характерные свойства распределения СВ, называются числовыми характеристиками (ЧХ) СВ. Наиболее важные среди них математическое ожидание и дисперсия.

Математическое ожидание случайной величины

Рассмотрим отдельно случай ДСВ и НСВ.

Пусть - ДСВ с конечным множеством возможных значений и - вероятности, с которыми эти значения принимаются, то есть задан закон распределения ДСВ:

Предположим, что над СВ произведено независимых наблюдений, в результате которых значение появилось раз, - раз,…, - раз (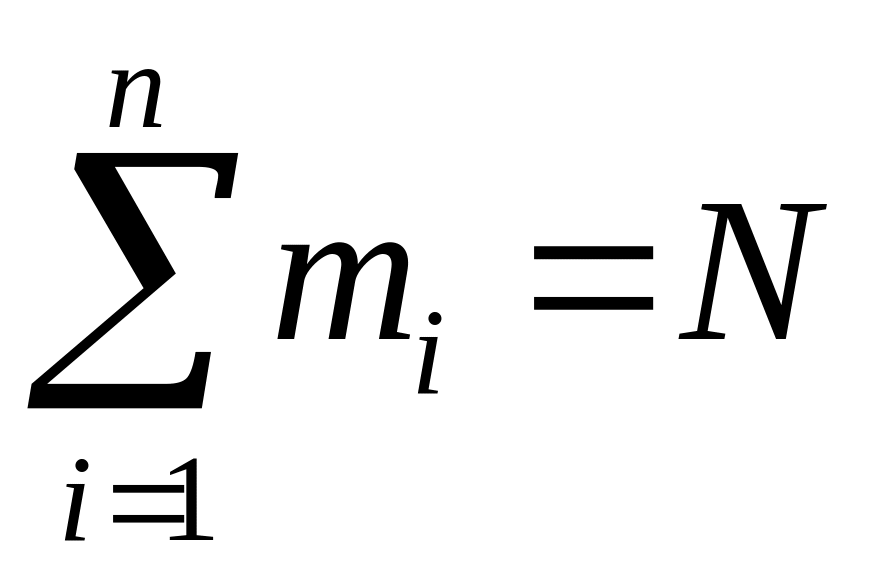 ). Тогда среднее значение СВ (среднее арифметическое) по результатам наблюдений можно записать в виде:

,

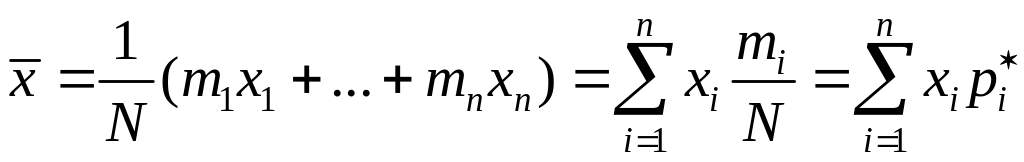где - статистическая вероятность (относительная частота) события . Известно, что при большом близка к истинной вероятности . Поэтому, если наблюдения над СВ не производятся, то за ее среднее значение целесообразно принять величину .

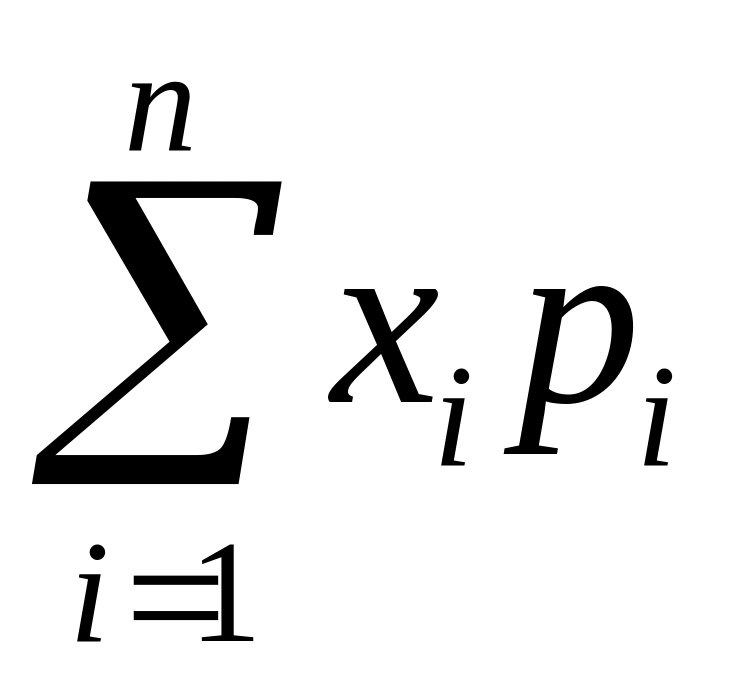Определение. Математическим ожиданием ДСВ , принимающей значения с вероятностями , называется величина

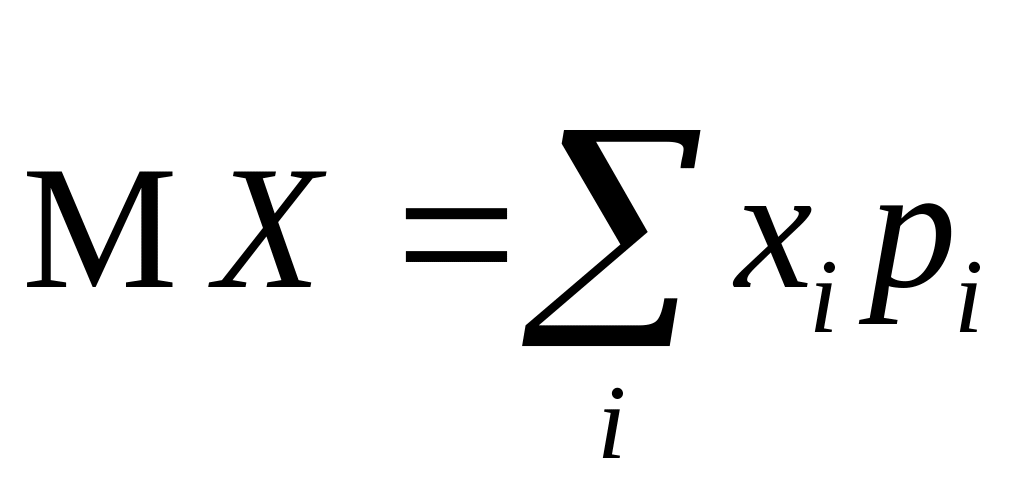, (2.7)

если ряд в правой части абсолютно сходится: .

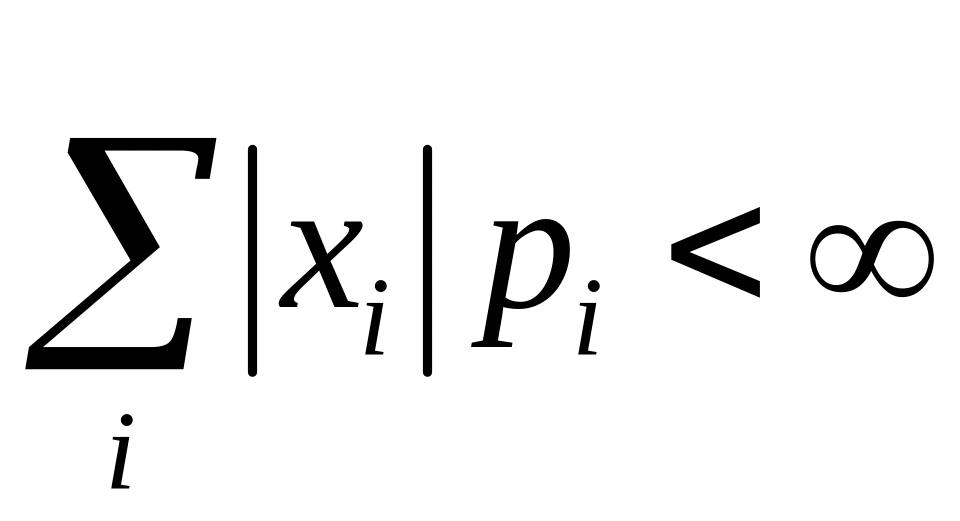Если ряд в правой части абсолютно расходится, то говорят, что математического ожидания у ДСВ не существует.

Замечание. Естественно, что вопрос о сходимости ряда встает только в случае, когда множество возможных значений ДСВ бесконечно (но счетно). У ДСВ, принимающей конечное число значений, математическое ожидание существует всегда.

Пусть теперь - НСВ с ПВ . Для определения МО построим следующую ДСВ , аппроксимирующую НСВ .

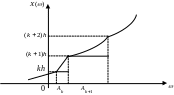
Для некоторого рассмотрим точки вида на числовой прямой и положим

, если , .

СВ принимает значения с вероятностями

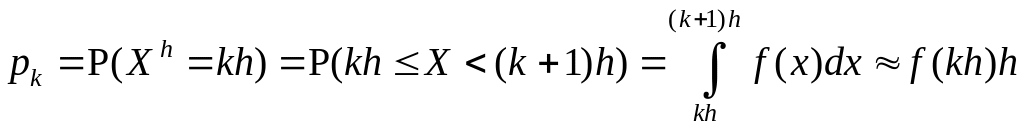
(при малом ), .

При любом и при ДСВ все точнее аппроксимирует НСВ . При этом

,

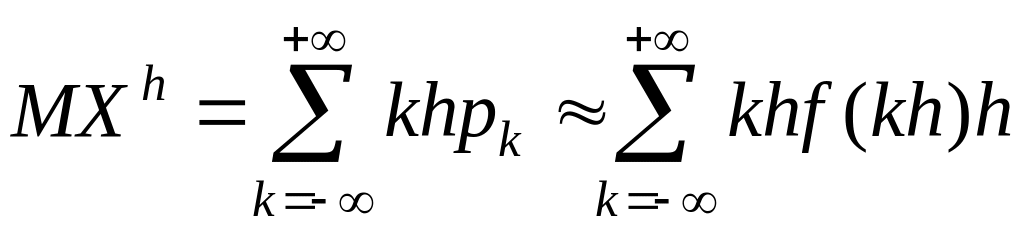если ряд сходится абсолютно. Последняя сумма является интегральной суммой для 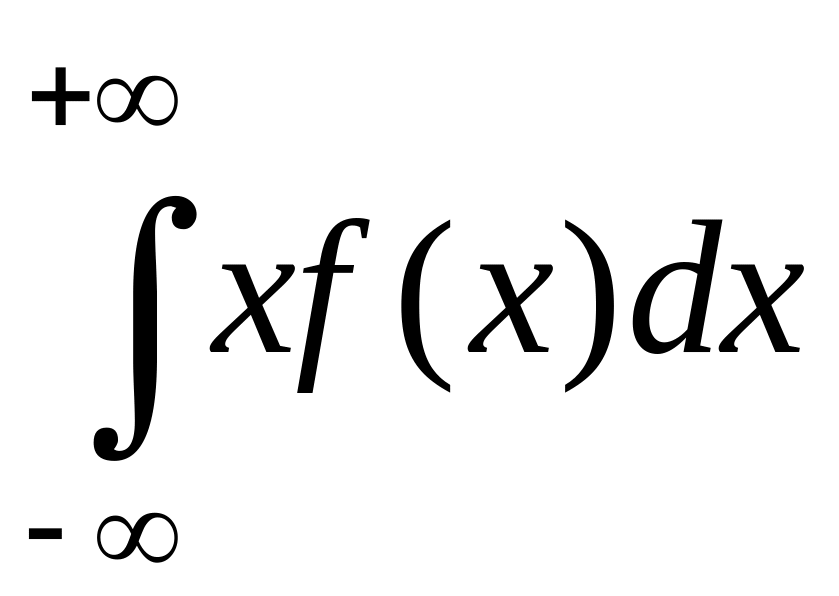, который и следует считать МО НСВ .

Определение. Математическим ожиданием НСВ с плотностью вероятностей называется величина

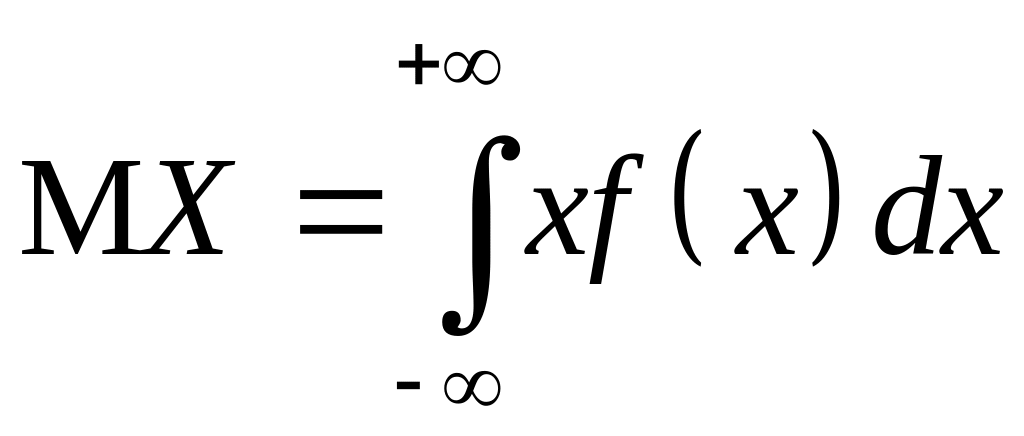, (2.8)

если интеграл в правой части абсолютно сходится: .

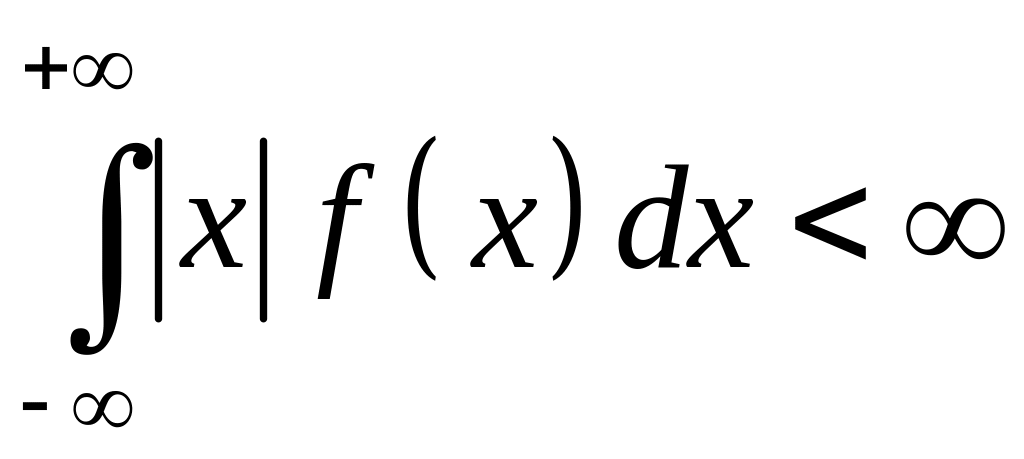Если интеграл в правой части абсолютно расходится, то говорят, что математического ожидания у НСВ не существует.

Замечание. Формулы (2.7) и (2.8) для МО ДСВ и НСВ можно объединить в одну, записав МО в виде

,

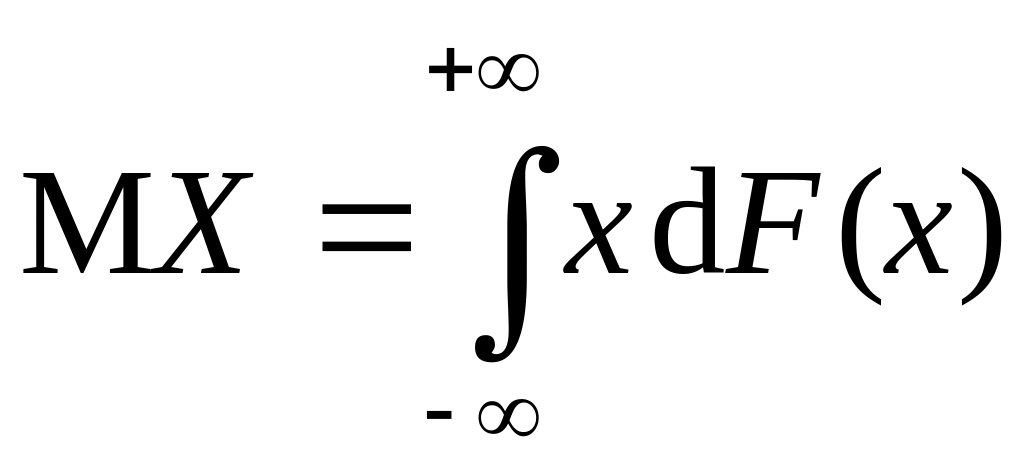где последний интеграл понимается в смысле Римана-Стилтьеса по ФР (подробнее см. учебник Гнеденко Б.В.).

Механическая интерпретация МО. Если закон распределения интерпретировать как распределение единичной массы вдоль оси абсцисс, то МО – координата центра тяжести (центра масс).

Геометрическая интерпретация МО. МО – среднее значение СВ, около которого группируются другие ее значения (иногда вместо МО СВ говорят среднее СВ ).

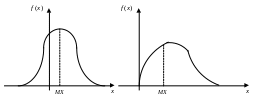
Основная теорема о МО.

Пусть - некоторая СВ, ЗР которой известен (дискретный или непрерывный), - неслучайная функция, область определения которой содержит множество возможных значений СВ . Рассмотрим СВ , являющуюся функцией от СВ .

Как можно найти ?

Есть два способа:

а) по ЗР СВ ищется ЗР СВ и используются стандартные формулы (2.7) и (2.8);

б) с помощью основной теоремы о МО (ОТМО).

Теорема. (ОТМО, теорема о замене переменных, без доказательства)

Пусть - некоторая СВ, ЗР которой известен, СВ является функцией от СВ .

1. Если СВ является дискретной, принимающей значения с вероятностями , , и при этом ряд абсолютно сходится ( ), то у СВ существует МО и

.

2. Если СВ является непрерывной с ПВ и интеграл 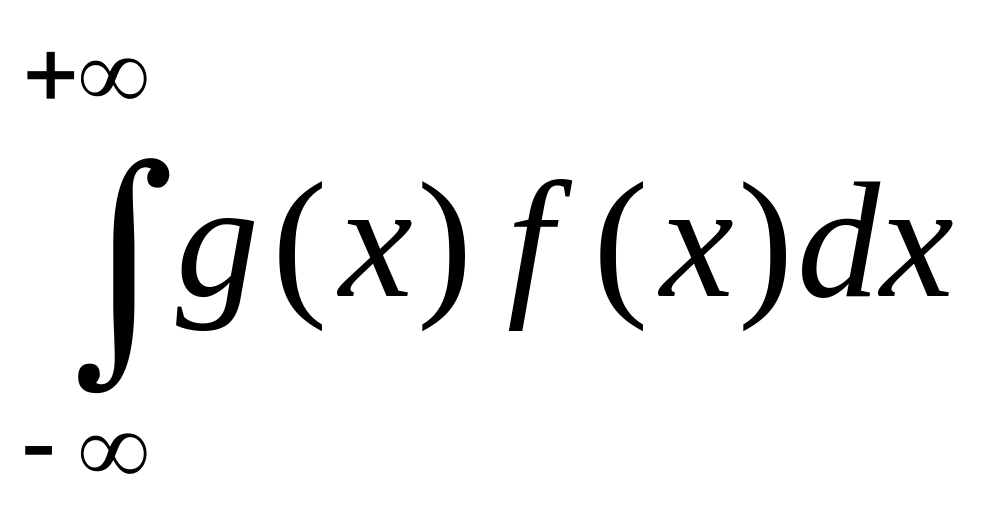абсолютно сходится ( 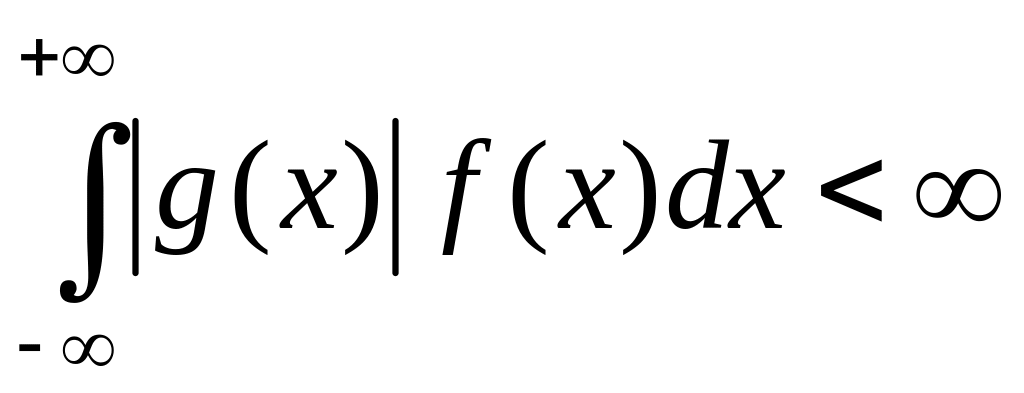), то у СВ существует МО и

.

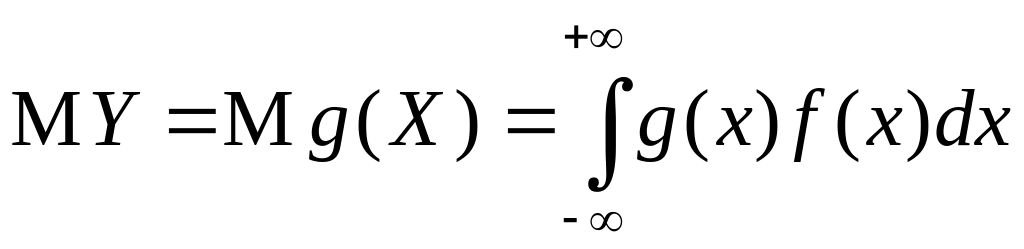Смысл ОТМО: Для нахождения МО СВ , являющейся функцией от СВ , не требуется знать ЗР СВ , достаточно лишь знать ЗР СВ .

Свойства МО.

1. МО постоянной равно этой постоянной: .

2. Постоянная выносится за знак МО:

.

▲ Следует из ОТМО при ■.

3. МО суммы любых СВ и равно сумме их МО:

.

▲ Следует из свойств линейности рядов и интегралов ■.

4. Если , то и .

Если и при этом , то .

▲ Следует из определения МО для ДСВ и НСВ ■.

Следствие. Если , то .

▲ Достаточно применить свойство 4 к СВ ■.

5.

▲ Следует из того, что для любого . Поэтому в силу свойства 4 МО , то есть ■.

Замечание. Свойство 5 справедливо и в более общем виде:

Для любой выпуклой вниз функции справедливо неравенство:

(неравенство Йенсена).