
- •390005, Рязань, ул. Гагарина, 59/1.
- •1.8. Разложение функции в ряд Тейлора
- •1.9. Приложения рядов для приближенных вычислений
- •2.3. Понижение порядка в дифференциальных уравнениях
- •2.5. Подбор частного решения лнду по виду правой части
- •3.3. Вычисление тройных интегралов в декартовой системе координат
- •3.4. Вычисление двойных интегралов в полярной системе координат
- •3.5. Вычисление тройных интегралов в цилиндрической и сферической системах координат
- •3.6. Криволинейный интеграл первого рода
- •3.7. Криволинейные интегралы второго рода
- •1.2. Признак Даламбера
- •1.3. Радикальный признак Коши
- •1.4. Интегральный признак Коши
- •1.5. Абсолютная и условная сходимость
- •1.6. Область сходимости степенного ряда
- •3.5. Вычисление тройных интегралов в цилиндрической и сферической системах координат
- •3.6. Криволинейный интеграл первого рода
- •3.7. Криволинейные интегралы второго рода
3784
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ
РЯДЫ.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ
ИНТЕГРАЛЫ
Типовые задачи
Рязань 2006
УДК 517.5
Ряды. Дифференциальные уравнения. Кратные и криволинейные интегралы: Типовые задачи / Рязан. гос. радиотехн. акад.; Сост.: И.П. Карасёв, Н.В. Ёлкина, С.С. Крыгина, Г.С. Лукьянова, Т.Н. Чернецова. Рязань, 2006. 48 c.
Приведены примеры и задачи для зачетов и экзаменов по математике.
Рекомендуется преподавателям кафедры высшей математики и студентам всех специальностей дневной формы обучения.
Ряды, дифференциальные уравнения, интегралы
Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.
Рецензент: кафедра высшей математики Рязанской государственной радиотехнической академии (зав. кафедрой канд. экон. наук, доц. А.И. Новиков)
Ряды. Дифференциальные уравнения.
Кратные и криволинейные интегралы
Составители: К а р а с ё в Иван Петрович
Ё л к и н а Наталия Викторовна
К р ы г и н а Светлана Степановна
Л у к ь я н о в а Галина Сергеевна
Ч е р н е ц о в а Татьяна Николаевна
Редактор Н.А. Орлова
Корректор С.В. Макушина
Подписано в печать 06.02.06. Формат бумаги 6084 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 3.0.
Уч.-изд. л. 3.0. Тираж 60 экз. Заказ
Рязанская государственная радиотехническая академия.
390005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Исследование рядов с помощью теорем сравнения
1.
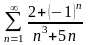 . 2.
. 2.
 . 3.
. 3.
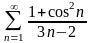 .
.
4.
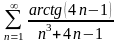 . 5.
. 5.
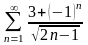 . 6.
. 6.
 .
.
7.
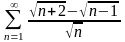 .
8.
.
8.
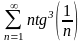 . 9.
. 9.
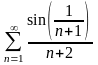 .
.
10.
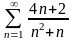 . 11.
. 11.
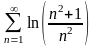 . 12.
. 12.
 .
.
13.
 .
14.
.
14.
 .
15.
.
15.
 .
.
16.
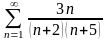 . 17.
. 17.
 . 18.
. 18.
 .
.
19.
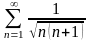 . 20.
. 20.
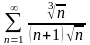 . 21.
. 21.
 .
.
22.
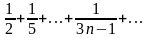 23.
23.
 .
.
24.
 . 25.
. 25.
 .
.
1.2. Признак Даламбера
1.
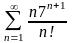 . 2.
. 2.
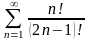 .
3.
.
3.
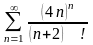 .
4.
.
4.
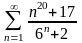 .
.
5.
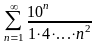 . 6.
. 6.
 . 7.
. 7.
 . 8.
. 8.
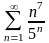 .
.
9.
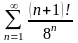 . 10.
. 10.
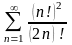 .
11.
.
11.
 .
12.
.
12.
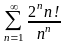 .
.
13.
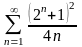 . 14.
. 14.
 . 15.
. 15.
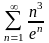 . 16.
. 16.
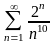 .
.
17.
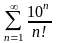 .
18.
.
18.
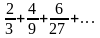 .
19.
.
19.
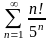 .
20.
.
20.
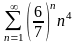 .
.
21.
 . 22.
. 22.
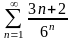 .
.
1.3. Радикальный признак Коши
1.
 . 2.
. 2.
 . 3.
. 3.
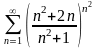 .
.
4.
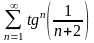 . 5.
. 5.
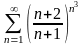 . 6.
. 6.
 .
.
7.
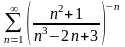 .
8.
.
8.
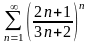 .
9.
.
9.
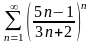 .
.
10.
 .
11.
.
11.
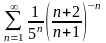 .
12.
.
12.
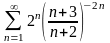 .
.
13.
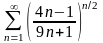 . 14.
. 14.
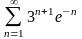 .
15.
.
15.
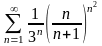 .
.
16.
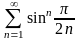 . 17.
. 17.
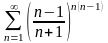 .
18.
.
18.
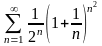 .
.
19.
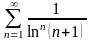 . 20.
. 20.
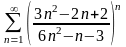 .
.
21.
 . 22.
. 22.
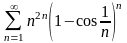 .
.
1.4. Интегральный признак Коши
1.
 . 2.
. 2.
 . 3.
. 3.
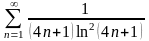 .
.
4.
 . 5.
. 5.
 .
.
6.
 . 7.
. 7.
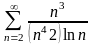 .
.
8.
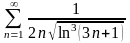 . 9.
. 9.
 . 10.
. 10.
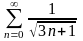 .
.
11.
 .
12.
.
12.
 .
13.
.
13.
 .
.
14.
 .
.
15.
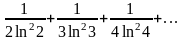 .
16.
.
16.
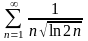 .
.
17.
 . 18.
. 18.
 . 19.
. 19.
 .
.
20.
 .
21.
.
21.
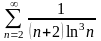 .
22.
.
22.
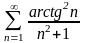 .
.
1.5. Абсолютная и условная сходимость
знакопеременных числовых рядов
1.
 . 2.
. 2.
 . 3.
. 3.
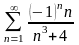 .
.
4.
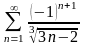 . 5.
. 5.
 . 6.
. 6.
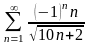 .
.
7.
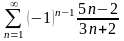 . 8.
. 8.
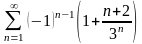 .
.
9.
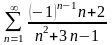 . 10.
. 10.
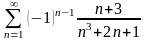 .
.
11.
 . 12.
. 12.
 .
.
13.
 . 14.
. 14.
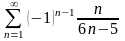 .
.
15.
 . 16.
. 16.
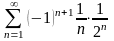 .
.
17.
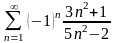 . 18.
. 18.
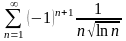 .
.
19.
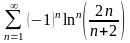 . 20.
. 20.
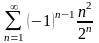 .
.
21.
 . 22.
. 22.
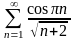 .
.
23.
 . 24.
. 24.
 .
.
25.
 . 26.
. 26.
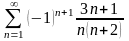 .
.
1.6. Область сходимости степенного ряда
1.
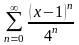 . 2.
. 2.
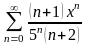 . 3.
. 3.
 .
.
4.
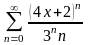 . 5.
. 5.
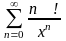 . 6.
. 6.
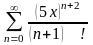 .
.
7.
 . 8.
. 8.
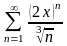 . 9.
. 9.
 .
.
10.
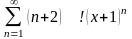 .
11.
.
11.
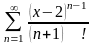 . 12.
. 12.
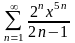 .
.
13.
 . 14.
. 14.
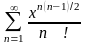 . 15.
. 15.
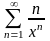 .
.
16.
 . 17.
. 17.
 . 18.
. 18.
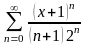 .
.
19.
 . 20.
. 20.
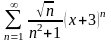 .
.
21.
 . 22.
. 22.
 . 23.
. 23.
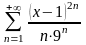 .
.
24.
 . 25.
. 25.
 . 26.
. 26.
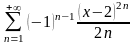 .
.
1.7. Применение почленного интегрирования и
дифференцирования для нахождения суммы ряда
Найти сумму ряда.
1.
 .
2.
.
2.
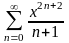 .
3.
.
3.
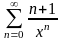 .
4.
.
4. .
5.
.
5.
 .
.
6.
 .
7.
.
7.
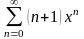 .
8.
.
8.
 .
.
9.
 .
10.
.
10.
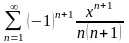 .
.
11.
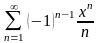 . 12.
. 12.
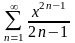 . 13.
. 13.
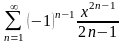 .
.
14.
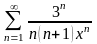 .
15.
.
15.
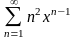 .
16.
.
16.
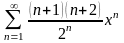 .
.
1.8. Разложение функции в ряд Тейлора
Разложить
функцию
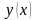 в ряд по степеням
в ряд по степеням
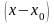 ,
указать область сходимости ряда.
,
указать область сходимости ряда.
1.
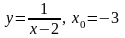 . 2.
. 2.
 .
.
3.
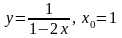 . 4.
. 4.
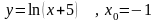 .
.
5.
 . 6.
. 6.
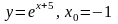 .
.
7.
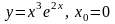 . 8.
. 8.
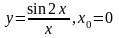 .
.
9.
 . 10.
. 10.
 .
.
11.
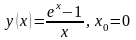 . 12.
. 12.
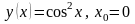 .
.
13.
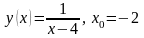 . 14.
. 14.
 .
.
15.
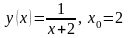 . 16.
. 16.
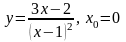 .
.
17.
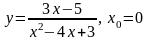 . 18.
. 18.
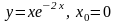 .
.
19.
 .
.
1.9. Приложения рядов для приближенных вычислений
1.
Вычислить
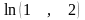 с точностью
с точностью
 .
.
2.
Вычислить
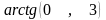 с точностью
.
с точностью
.
3.
Вычислить
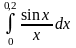 с точностью
.
с точностью
.
4.
Вычислить
 с точностью
.
с точностью
.
5.
Вычислить
 с точностью
.
с точностью
.
6.
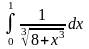 ,
вычислить, взяв 3 члена, оценить
погрешность.
,
вычислить, взяв 3 члена, оценить
погрешность.
7.
 с точностью 0,0001.
с точностью 0,0001.
8.
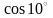 с точностью 0,0001.
с точностью 0,0001.
9.
 с точностью 0,0001.
с точностью 0,0001.
10.
 с точностью до 0,0001.
с точностью до 0,0001.
11.
Вычислить
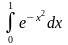 с точностью
с точностью
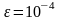 .
.
12.
Вычислить
 с точностью до 0,0001.
с точностью до 0,0001.
13.
Вычислить
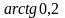 с точностью до 0,0001.
с точностью до 0,0001.
14.
Вычислить
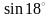 с
точностью до 0.0001.
с
точностью до 0.0001.
15.
Вычислить
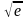 с точностью до 0.0001.
с точностью до 0.0001.
2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
2.1. Однородные дифференциальные уравнения
1-го порядка
1.
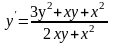 . 2.
. 2.
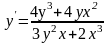 .
.
3.
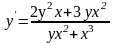 . 4.
. 4.
 .
.
5.
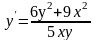 . 6.
. 6.
 .
.
7.
 . 8.
. 8.
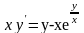 .
.
9.
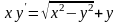 . 10.
. 10.
 .
.
11.
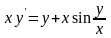 ,
,
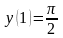 . 12.
. 12.
 .
.
13.
 . 14.
. 14.
 .
.
15.
 . 16.
. 16.
 .
.
17.
 .
18.
.
18.
 .
.
19.
 ,
,
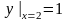 .
.
20.
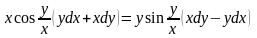 .
.
2.2. Линейные дифференциальные уравнения
первого порядка
1.
 ,
,
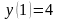 . 2.
. 2.
 .
.
3.
 ,
,
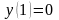 . 4.
. 4.
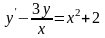 .
.
5.
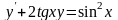 . 6.
. 6.
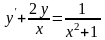 .
.
7.
 . 8.
. 8.
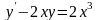 .
.
9.
 . 10.
. 10.
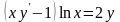 .
.
11.
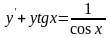 . 12.
. 12.
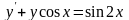 .
.
13.
 . 14.
. 14.
 .
.
15.
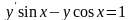 ,
,
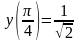 .
.
16.
 . 17.
. 17.
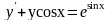 ,
,
 .
.
18.
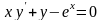 ,
,
 .
.
19.
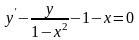 ;
.
;
.
20.
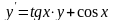 . 21.
. 21.
 .
.
