Раздел 2. Приложение математического анализа функций многих переменных к задачам экономики и управления

2.1. Производственная функция Кобба—Дугласа.

В 1927 г. экономист Пол Дуглас, анализируя динамику изменения индексов реального объема производства, реальных капитальных затрат и реальных затрат труда в промышленности США в период 1899—1922 гг., обнаружил, что временная зависимость логарифмов этих величин характеризуется интересной закономерностью: расстояние от точек графика показателей выпуска (Q) до точек графиков показателей затрат труда (K) и капитала (L) составляет постоянную пропорцию. Математик Чарльз Кобб предложил математическую формулу, описывающую такую зависимость:

Q = AK^L^1 . (2.1)

По оценкам Ч. Кобба и П. Дугласа, величина  = 1/4 (современный расчет по исходным данным, использованным Ч. Коббом и П. Дугласом, методом наименьших квадратов, дает именно это значение  = 0,25 и, соответственно, 1 = 0,75; если использовать более общую аппроксимирующую формулу Q = AK^L^, то получаем близкие значения  = 0,23 и  = 0,81).

Функцию (2.1) Q = AK^L^1 можно рассматривать как функцию двух переменных K и L, к которой применима теория функций многих переменных. Ниже будут рассмотрены основные экономические понятия, связанные с этой теорией.

2.2. Основные экономические понятия, связанные с производственной функцией.

В общем случае производственная функция описывает зависимость объема выпускаемой продукции от затрачиваемых или используемых ресурсов, и может быть функцией не двух, а большего числа переменных. Так, в рамках действующего предприятия в качестве затрачиваемых или используемых ресурсов могут фигурировать затраты рабочего времени, сырья, комлектующих изделий, энергии, основного капитала, т.е. пять переменных. Если производственная функция описывает экономику региона, то в качестве ресурсов можно рассматривать основной капитал, живой труд и природные ресурсы, а значением функции является совокупный продукт региона.

Для простоты рассмотрим общий вид производственной функции двух переменных Q = f(K, L), описывающей зависимость выпуска продукции от вложенного капитала K и затраченного труда L. График производственной функции двух переменных — поверхность в трехмерном пространстве. Линия уровня производственной функции, т.е. линия, в каждой точке которой объем выпуска при разных значениях и один и тот же, называется изоквантой или кривой безразличия производства. Уравнение изокванты имеет вид f(K, L) = const.

Изокванты не пересекаются; большему объему производства отвечают изокванты, более удаленные от начала координат; касательные к изоквантам имеют отрицательный угловой коэффициент.

При исследовании свойств производственной функции используют т.н. предельные величины, математически являющиеся частными производными.

Предельным продуктом капитала называют предел отношения приращения количества произведенной продукции к вызвавшему это приращение приросту вложенного капитала, т.е. частная производная производственной функции Q = f(K, L) по переменной K. В отличии от математического понятия частной производной, предельный продукт капитала является размерной величиной:

= . (2.2)

Аналогично, предельным продуктом труда называют предел отношения приращения количества произведенной продукции к вызвавшему это приращение приросту вложенного труда, т.е. частная производная производственной функции Q = f(K, L) по переменной L. Предельный продукт труда также является размерной величиной:

= . (2.3)

При одновременном изменении вложенного труда и капитала приращение выпуска можно приближенно вычислить по формуле, аналогичной (1.4):

. (2.4)

Величина , вычисленная в точках изокванты, называется коэффициентом заменяемости ресурсов. Он показывает, на сколько единиц нужно увеличить вложение капитала при уменьшении на единицу вложенного труда с тем, чтобы выпуск не изменился. Геометрический смысл коэффициента заменяемости ресурсов — угловой коэффициент касательной к изокванте. Используя теорему для производной неявной функции Q(K, L) = const, можно получить рабочую формулу для вычисления коэффициента заменяемости ресурсов:

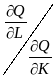= . (2.5)

Пример 3. Построить двумерный график производственной функции Q = K^1/4L^3/4, представив его в виде семейства изоквант в области изменения переменных K = {1, 3}и L = {1, 4}. Рассчитать предельные продукты труда и капитала, а также коэффициент заменяемости ресурсов в точке K = 2, L = 3.

Решение. Так как производственная функция Q = K^1/4L^3/4 монотонно возрастает в области ее определения, то ее наибольшее и наименьшее значения отвечают величинам

Q_мин = (K_мин)^1/4 (L_мин)^3/4 = 1^1/41^3/4 = 1;

Q_макс = (K_макс)^1/4 (L_макс)^3/4 = 3^1/44^3/4 = 1,3162,828 = 3,72,

т.е. область изменения функции Q = {1; 3,72}, поэтому достаточно построить графики двух изоквант Q = 2 и Q = 3.

Из уравнений изоквант K^1/4L^3/4 = 2 и K^1/4L^3/4 = 3 получаем соответственно взаимосвязь между переменными K и L при постоянном выпуске:

K = 16/L³ ; K = 81/L³.

На рис. 2.1 представлен график производственной функции Q = K^1/4L^3/4 в виде семейства изоквант (дополнительно построены также изокванты K^1/4L^3/4 = 1,5; K^1/4L^3/4 = 2,5; K^1/4L^3/4 = 3,5).

Рис. 2.1. Линии уровня производственной функции Q = K1/4L3/4, построенные средствами программы Mathcad 7.0 (переменная L — горизонтальная ось, переменная К — вертикальная ось)

Из наклона изоквант к горизонтальной (затраты капитала) и вертикальной (затраты труда) осям можно заключить, что более сильное влияние на выпуск продукции оказывают затраты труда. В точке с координатами (2, 3) выпуск продукции примерно равен 2,7 единиц (определено визуально по графику). Более точный расчет дает подстановка этих значений в формулу: Q(2, 3) = 2^1/43^3/4 = 1,1892,279 = 2,71.

Для расчета предельных продуктов труда и капитала используем формулу производной степенной функции .

Предельный продукт труда = = =3/4 . Подставляя K = 2, L = 3, получаем: (2, 3) = 3/42^1/4/3^1/4 = 0,751,189/1,316 = 0,68 ед. продукции на ед. труда.

Предельный продукт капитала = = =1/4 . Подставляя K = 2, L = 3, получаем: (2, 3) = [(1/4)/2^3/4]3^3/4= (0,25/1,682)2,279= 0,34 ед. продукции на ед. капитала.

Полученные результаты интерпретируются так: производство продукции Q, характеризующееся величинами капитала K = 2 и труда L = 3, при увеличении труда L на одну ед. увеличивается на 0,68 ед., а при увеличении капитала K на одну ед. увеличивается на 0,34 ед. Таким образом, увеличение труда является более эффективным.

Коэффициент заменяемости ресурсов определяется по формуле (2.5). Запишем ее с учетом обозначений = и = . Тогда получаем:

= = .

Подставляя найденные значения предельных продуктов труда и капитала в точке K = 2, L = 3, получаем: R(2, 3) = = 0,68/0,34 = 2. Это означает, что для того, чтобы выпуск продукции не изменился, надо при уменьшении на единицу вложенного труда увеличить вложение капитала на две единицы.

2.3. Эластичность производственной функции (эластичность выпуска). Оценка эффективности производства

Рассмотренные в предыдущем подразделе экономические понятия имеют размерность, что не вполне удобно для анализа взаимосвязи относительных изменений переменных. Вводят понятия: эластичность выпуска по труду E_L и эластичность выпуска по капиталу E_K, определяемые формулами

E_L = ; (2.6)

E_K = . (2.7)

Безразмерные показатели E_L и E_K показывают, на сколько процентов произойдет относительное увеличение выпуска при относительном увеличении соответствующего ресурса на 1%.

Сумма значений эластичности выпуска по всем ресурсам называется эластичностью производства:

E = E_K + E_L. (2.8)

Для эластичности _KL предельной нормы замещения труда капиталом справедливо соотношение:

_KL = . (2.9)

Эффективность производственного процесса (эффект от масштаба производства) можно оценить математически, увеличив одновременно все ресурсы в t раз. Если использовать более общую аппроксимирующую формулу Кобба—Дугласа Q = AK^L^, получаем: Q (tK, tL) = AK^t^L^t^ = t^t^ Q (K, L) = t^+ Q (K, L). Отсюда вытекает, что если  и  в сумме превышают единицу, то говорят, что производственная функция имеет возрастающий эффект от масштаба производства (если ресурсы K и L увеличиваются в некоторой пропорции, то выпуск Q растет в большей пропорции). Если их сумма меньше, чем единица, то имеет место убывающий эффект от масштаба производства.

В своей первой статье Ч. Коббс и П. Дуглас описывали производственную функцию в виде (2.1), предполагающем постоянную отдачу от масштаба:  и  в сумме точно составляют единицу. Впоследствие они ослабили это допущение, предпочитая оценивать степень отдачи от масштаба производства. Как указывалось нами ранее, при обработке исходных данных, использованных Ч. Коббсом и П. Дугласом, методом наименьших квадратов, получаем значения  = 0,23 и  = 0,81. Сумма  и , равная 1,04, лишь несколько превышает единицу, т.е. первоначальное предположение Ч. Коббса и П. Дугласа о постоянной отдаче от масштаба было вполне оправдано.

Пример 4. Рассчитать эластичность выпуска по труду и капиталу для производственной функции Q = K^1/4L^3/4 в точке K = 2, L = 3. Оценить эффект от масштаба производства.

Решение. Эластичность выпуска по труду определяется формулой (2.6). Так как предельный продукт труда = =3/4 , получаем:

E_L = = = (3/4 ) = (L / K^1/4L^3/4)(3/4 ) = 3/4.

Эластичность выпуска по капиталу определяется формулой (2.7). Так как предельный продукт капитала = =1/4 , получаем:

E_K = = = (1/4 ) = (K / K^1/4L^3/4)(1/4 ) = 1/4.

Таким образом, эластичность выпуска по труду и капиталу в случае производственной функции Кобба—Дугласа вида Q = AK^L^ не зависит от точки производства и равна показателям степени при соответствующих переменных  = 0,75 и  = 0,25 соответственно.

Сумма значений эластичности выпуска по всем ресурсам (эластичность производства) равна  +  = 1, т.е. в данном случае имеет место постоянная отдача от масштаба производства.

Для эластичности _KL предельной нормы замещения труда капиталом в общем случае производственной функции вида Q = AK^L^ получаем:

_KL = =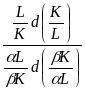 = 1,

т.е. для функции Кобба—Дугласа эластичность предельной нормы замещения труда капиталом постоянна и равна единице. Это важнейшее свойство функции Кобба—Дугласа.