Задача 24.

Страховщик заключает договоры страхования гражданской ответственности предприятий, эксплуатирующих опасные производственные объекты (таблица 3).

Рассчитать: 1) брутто-ставку (Т_б);

2. доли тарифной ставки (Т_б) для формирования соответствующих страховых фондов, если среднее соотношение ущерба жизни или здоровью граждан, имуществу юридических лиц или физических лиц и ущерба, нанесенного окружающей среде оценивается: 1:3:5.

Таблица 3 Исходные данные

Вид страхования	Страхование ГО предприятий					Страхование имущества юридических лиц				Страхование граждан от несчастных случаев
Вариант	I	II	III	IV	I		II	III	IV	I	II	III	IV
Вероятность страхового случая, %	1,3	1,1	1,2	1,4	1,5		1,2	2,4	1,7	3,1	2,8	3,5	4,2
Средняя страховая сумма, тыс.руб.	2400	3200	3400	2900	500		480	610	580	140	120	75	50
Средняя страховая выплата, тыс. руб.	1500	1800	1900	1700	380		355	395	289	56	42	31	18
Средний разброс возмещений, тыс.руб.	-	-	-	-	-		-	-	-	30	25	21	7
Коэффициент гарантии безопасности,	1,645	1,3	1,3	1,645	1,3		1,645	1,3	1,645	1,3	1,645	1,0	1,3
Ожидаемое количество договоров, шт	40	30	20	50	100		1500	2000	1200	5000	6000	7200	8000
Нагрузка, %	30	30	40	35	28		30	40	35	30	25	35	30

По договору страхования при наступлении страхового случая страховщик возмещает, помимо прямого ущерба, также и дополнительные расходы, включающие:

а) расходы страхователя по очистке загрязненной территории и приведение ее в состояние, соответствующее установленным нормативам;

б) расходы страхователя, связанные с предварительным выяснением причин и последствий страхового случая;

в) необходимые расходы страхователя по спасению жизни и имущества потерпевших третьих лиц, осуществлению мер по уменьшению ущерба, причиненного страховым случаем;

г) судебные издержки и расходы страхователя по делам о возмещении вреда, причиненного страховым случаем, если эти издержки вместе с суммой страховой выплаты не превышают установленного лимита ответственности страховщика.

Рассчитать доли тарифных ставок для формирования соответствующих страховых фондов в целях возмещения дополнительных расходов, если по экспертным оценкам, выплаты страховщика делятся в соответствии с перечнем по пункту (а) - 10 %, по пункту (б) - 4 %, по пункту (в) - 5 %, по пункту (г) - 3 %.

Задача 25.

Рассчитать брутто-ставку (Т_б), если страховщик заключает договоры страхования имущества юридических лиц (таблица 3).

Задача 26.

Рассчитать брутто-ставку (Т_б), если страховщик заключает с гражданами договоры страхования от несчастных случаев (таблица 3).

Задача 27.

Страховщик проводит все ранее указанные виды страхования (таблица 3), т.е. в страховом портфеле страховщика разнородные риски. Рассчитать коэффициент ; нетто-ставку для любого вида страхования, составляющего страховой портфель; соответствующие брутто-ставки со 100 руб. страховой суммы.

Задача 28.

Рассчитать прогнозную брутто-ставку, если страховая компания располагает данными о сумме страховых возмещений и совокупной страховой сумме по рискам, принятым на страхование за ряд лет (таблица 4).

Таблица 4 Исходные данные

Вариант	Порядковый номер года, (i)	Общая страховая сумма (S), тыс.руб.	Страховое возмещение (SB), тыс.руб.	Нагрузка в структуре брутто-ставки, (f), %
А	1	2278	410	30
	2	2942	765
	3	2755	799
	4	3094	1114
	5	3346	1305
Б	1	2109	390	25
	2	2791	805
	3	2802	863
	4	2670	986
	5	3160	1274
В	1	2391	504	40
	2	2905	692
	3	2680	704
	4	3057	1085
	5	3442	1361
Г	1	2306	446	35
	2	3015	791
	3	2802	821
	4	3204	1224
	5	3432	1403

Расчет нетто-ставки производится в следующей последовательности:

а) по каждому году рассчитывается фактическая убыточность страховой суммы (у) как отношение страхового возмещения к общей страховой сумме застрахованных рисков (S_B /S);

б) на основании полученного ряда исходных данных рассчитывается прогнозируемый уровень убыточности страховой суммы, для чего используется модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваются на основе линейного уравнения:

= а₀+а₁i,

где - выравненный показатель убыточности страховой суммы;

а₀, а₁ - параметры линейного тренда;

i - порядковый номер соответствующего года.

Параметры линейного тренда можно определить методом наименьших квадратов, решив следующую систему уравнений с двумя неизвестными:

а₀ · n + а₁ ,

а₀ а₁

где n - число анализируемых лет

у₆ =а₀+а₁ ∙6

в) для определения рисковой надбавки необходимо по следующей формуле рассчитать среднее квадратическое отклонение фактических значений убыточности от выравненных значений:

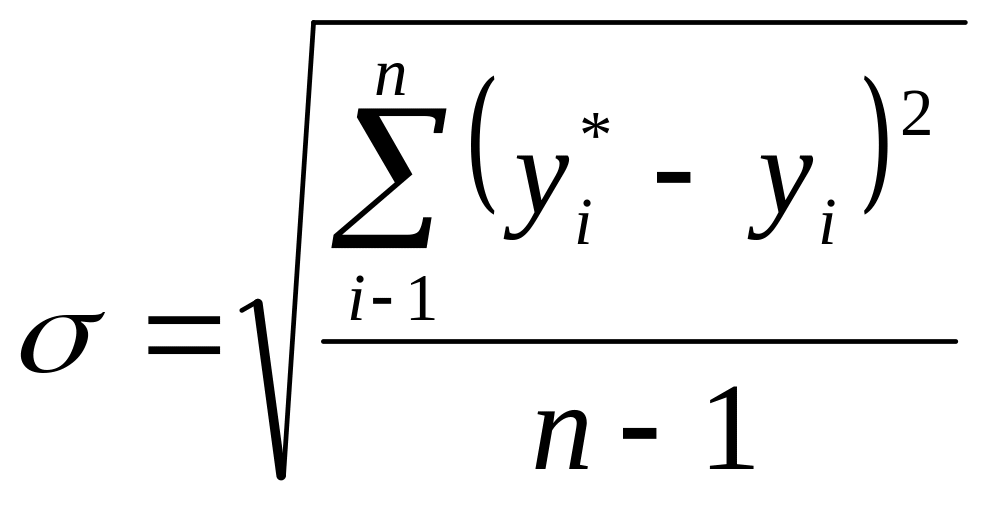
г) нетто-ставка рассчитывается следующим образом:

Т_n=y₆+β(γ;n)∙σ,

где β(γ;n) - коэффициент, используемый для исчисления размера рисковой надбавки. Величина β(γ;n) зависит от заданной гарантии безопасности γ (той вероятности , с которой собранных взносов хватит на выплаты страховых возмещений) и n - числа анализируемых лет, и может быть взята из таблицы 5.

Таблица 5 Исходные данные

γ n	0,8	0,9	0,95	0,975	0,99
3	2,972	6,649	13,640	27,448	68,740
4	1,592	2,829	4,380	6,455	10,448
5	1,184	1,984	2,850	3,854	5,500
6	0,980	1,596	2,219	2,889	3,900

Допустим, страховая компания считает необходимым с уровнем вероятности γ=0,9 быть уверена в том, что собранной суммы взносов будет достаточно для выплаты страховых возмещений. Тогда из таблицы 5 при γ=0,9 для n=5, β=1,984.