Министерство высшего и среднего специального

образования РСФСР

Архангельский ордена Трудового Красного Знамени

лесотехнический институт им. В.В.Куйбышева

МАГНИТНОЕ ПОЛЕ ТОКА

Методические указания

к выполнению лабораторных работ

Архангельск

1981

Рассмотрены и рекомендованы к изданию методической

комиссией химико-технологического факультета

Архангельского ордена Трудового Красного Знамени

лесотехнического института им.В.В.Куйбышева

6 октября 1979 г.

Составители:

Л.В.ФИЛИМОНЕНКОВА, Г.В.ЯБЛОНОВСКИЙ,

Л.Ф.СТЕПАНОВА, Ю.В.ЛОГИНОВ,

В.В.НЕКРАСОВ

Научный редактор

Б.К.СЕМЕНОВ, канд.хим.наук доцент

Рецензент

В.В.АПАНАСОВ, канд.техн.наук доцент

■ ■■■■.■ '■■'*■.■■■■ . ■ ■

УДК 538.1/2

Магнитное поле тока: Методические указания к выполнению лабораторных работ/ Филимоненкова Л.B._, Яблоновский Г.В., Степанова Л.Ф., Логинов Ю.В., Некрасов В.В. - Архангельск: РИО АЛТИ_, 1981. – 44 с. Подготовлены кафедрой физики АЛТИ.

Методические указания включают описание семи лаборатор­ных работ, связанных с изучением электромагнетизма в общем курсе физики, которые охватывают наиболее важные разделы программы по электричеству общего курса физики в технических вузах. Даны подробные теоретические сведения, порядок выполнения работ и обработки результатов эксперимента.

Предназначены для студентов I,II курсов всех факультетов дневной, вечерней и заочной форм обучения.

Ил.27. Табл.10. Библиогр, 3 назв.

 АЛТИ, I981

ЛАБОРАТОРНАЯ РАБОТА 2.2.1

ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ

ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ

Цель данной работы – определение горизонтальной составляющей индукции магнитного поля Земли при помощи тангенс-гальванометра.

При протекании постоянного электрического тока по проводнику в окружающем проводник пространстве создается магнитное поле.

Величину индукции магнитного поля, созданного элементом тока в некоторой точке пространства C, рассчитывают по закону Био-Савара-Лапласа:

(1.1)

В векторной форме этот закон имеет вид:

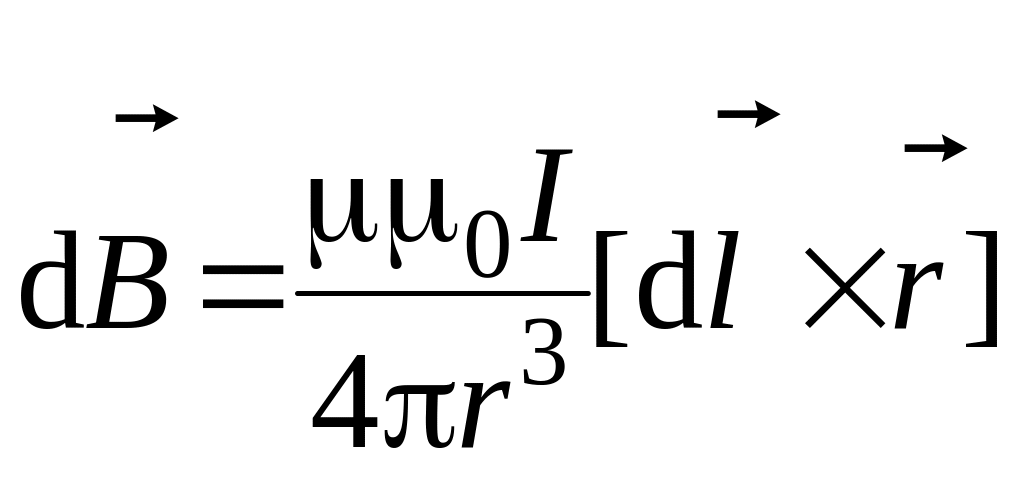, (1.2)

где μ – относительная магнитная проницаемость среды;

μ₀ − магнитная постоянная, которая в системе СИ равна

4π∙10^-7 Гн/м;

I – сила тока в проводнике;

dl – длина элемента с током;

- радиус-вектор, соединяющий элемент dl с точкой,

в которой создается индукция dB;

- угол, образованный элементом проводника с током и радиус-вектором .

Вектор индукции совпадает с нормалью к плоскости, которую образуют вектора и . Направление определяется векторным произведением (1.2). Индукция магнитного поля в центре кругового тока представляет собой суперпозицию векторов . Для точки в центре кругового тока величины r=const и . Результирующая индукции магнитного поля в центре кругового тока находится интегрированием:

(1.3)

Если вместо одного витка ток проходит по N одинаковым виткам, центры которых почти совпадают, то индукция магнитного поля в центре:

(1.4)

Вектор индукции направлен перпендикулярно плоскости витков.

Описание установки

Для экспериментального определения горизонтальной составляющей индукции магнитного поля Земли используется прибор, называемый тангенс-гальванометром (ТГ). Он состоит из витков радиусом r , в центре которых расположена магнитная стрелка. Магнитная стрелка расположена на вертикальной оси, закрепленной в корпусе, по периферии которого нанесены деления через 1⁰.

При отсутствии тока в витках на магнитную стрелку действует только магнитное поле Земли. Горизонтальной составляющей магнитного поля Земли , которую необходимо определить на данной установке, называется проекция вектора магнитной индукции Земли на горизонтальную плоскость в точке её определения.

Перед включением тока плос кость витков совмещают с плоскостью магнитного меридиана Земли. Для этого тангенс-гальванометр устанавливают так, чтобы ось магнитной стрелки находилась в плоскости витков. При таком расположении витков вектор индукции магнитного поля тока перпендикулярен горизонтальной составляющей магнитного поля Земли .

При пропускании тока по виткам на магнитную стрелку действует два магнитных поля: поле, созданное током в витках, и поле Земли. При одновременном действии и ось магнитной стрелки устанавливается по направлению результирующей этих векторов , как это показано на рис.1.1.

Из рис.1.1 видно, что модуль можно выразить через :

, (1.5)

то есть

(1.6)

Последнее уравнение является расчетным.

Порядок выполнения работы

1. Снять характеристики приборов.

2. Собрать установку по схеме, представленной на рис.1.2, где введены следующие обозначения: ТГ - тангенс-гальванометр; mA – миллиамперметр; R – реостат; Е – источник по стоянного тока; К – ключ для замыкания цепи.

Примечание. Сборку цепи производить при разомкнутом ключе К и полностью выведенном реостате.

3. Установить плоскость витков параллельно оси магнитной стрелки (в плоскости меридиана).

4. Замкнуть цепь, установить в цепи такой ток, чтобы магнитная стрелка отклонилась на угол и снять показания миллиамперметра.

5. Проделать аналогичные измерения, увеличивая угол φ до максимального отклонения 60⁰, снимая показания миллиамперметра.

6. Результаты измерений занести в таблицу.

φ, град
I, mA

Обработка результатов эксперимента

1. По уравнению (1.4) рассчитать индукцию магнитного поля в центре витков с током, внести результаты в таблицу.

2. Рассчитать горизонтальную составляющую магнитного поля Земли для всех значений I; φ, результаты занести в таблицу.

3. Найти среднее значение .

4. Рассчитать погрешность измерения .

Контрольные вопросы

1. Сформулировать закон Био-Савара-Лапласа.

2. Рассчитать индукцию магнитного поля в центре кругового тока.

3. Объяснить принцип действия тангенс-гальванометра.

4. Единицы измерения индукции магнитного поля.

5. На основании закона Био-Савара-Лапласа вывести уравнение для расчета напряженности магнитного поля, созданного бесконечно длинным прямым проводником с током.

6. Единицы измерения напряженности магнитного поля.

ЛАБОРАТОРНАЯ РАБОТА 2.2.3

ИССЛЕДОВАНИЕ ФЕРРОМАГНЕТИКОВ

При внесении в магнитное поле тело намагничивается. Намагниченное тело, находящееся во внешнем поле, создает свое собственное поле, которое в изотропных пара- и ферромагнитных телах направлено параллельно внешнему полю, в диамагнетиках – антипараллельно. Вектор магнитной индукции равен сумме векторов магнитной индукции внешнего магнитного поля и магнитной индукции собственного поля вещества :

.

Магнитная индукция B характеризует магнитное поле в веществе и связано с напряженностью H поля соотношением

. (3.1)

Для парамагнитных веществ μ немного больше единицы, например: μ (Al)=1,0000230; μ (Pt)=1,0003600. Для диамагнитных веществ μ немного меньше единицы, например:μ (Bi)=0,9998240; μ (NaCl)=0,9999874. Ферромагнитные вещества (железо, никель, кобальт и некоторые их сплавы и сплавы неферромагнитных элементов) обладают отличительными свойст вами:

1. Зависимость B от H для ферромагнетиков носит нелинейный характер. Кривая намагничивания довольно сильно возрастает в области слабых полей, после наступления насыщения (точка А) кривая переходит в прямую, где наблюдается линейная зависимость между B и H (рис.3.1).

2. Магнитная проницаемость фер ромагнетиков может достигать больших значений в зависимости от напряженности внешнего магнитного поля, зависимость μ=f (H) приведена на рис. 3.2.

3. Намагниченность ферромагнетиков сохраняется после снятия внешнего поля. При циклических изменениях поля зависимость B от H имеет вид кривой, называемой «петлей гистерезиса» (рис.3.3). 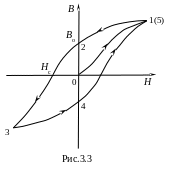Точка 2 на рис.3.3 характеризуется величиной остаточной индукции . Намагничивание обращается в нуль пол действием поля , имеющего направление, противоположное полю, вызвавшему намагничивание, и называется коэрцитивной силой.

Эти свойства ферромагнетиков объясняются доменной структурой. В ферромагнетиках существуют макроскопические области, называемые доменами. Домены имеют размеры порядка ( )см и представляют собой маленькие магнитики, в которых магнитные моменты атомов, в основном обусловленные спинами электронов, спонтанно (самопроизвольно) ориентированы в определенном направлении. Намагниченность в пределах каждого домена очень велика. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы беспорядочно, поэтому суммарный магнитный момент большого куска ненамагниченного ферромагнетика равен нулю. Когда образец помещается во внешнее магнитное поле, происходит ориентировка магнитных моментов доменов в направлении этого поля, в результате чего возникает макроскопическое намагничивание. Этим и объясняется быстрое изменение μ ферромагнетиков в слабых полях. При больших значениях напряженности H внешнего магнитного поля магнитные моменты доменов выстраиваются параллельно, наступает состояние магнитного насыщения.

Задание Б. Изучение зависимости индукции B магнитного поля и магнитной проницаемости железа от внешнего (намагничивающего) поля баллистическим методом (рис. 3.6).

Для снятия кривой намагничивания железа удобно иметь образец в форме кольца, являющегося сердечником тороида. При пропускании тока через обмотку тороида, намотанную равномерно вдоль всего сердечника, образуется магнитное поле, целиком сосредоточенное внутри железного кольца. Напряженность намагничивающего поля, создаваемого обмоткой тороида, определяется по формуле

, (3.6)

где n – число витков на единицу длины намагничивающей обмотки I (рис.3.6),

(3.7)

N₁ – полное число витков обмотки I;

l – длина средней линии сердечника тороида, диаметр которого d, l = πd.

Из формулы (3.6) видно, что , так как для данной намагничивающей катушки.

Измерение индукции (B) поля внутри сердечника можно произвести с помощью второй (индукционной) катушки, намотанной на тот же тороид и соединенной с баллистическим гальванометром (рис.3.6). При переключении тока в намагничивающей катушке I поток индукции в сердечнике изменяется. По закону Фарадея всякое изменение потока индукции через контур вызывает в последнем появление ЭДС индукции:

(3.8)

Выражение (3.8) дает значение ЭДС индукции, возникающей в одном витке индукционной катушки II. Мгновенное значение ЭДС индукции во всей катушке

,

где N₂ – число витков индукционной катушки.

При наличии ЭДС в индукционной катушке протекает ток, мгновенное значение которого определяется по формуле

.

Количество электричества, протекающего во время dt, равно:

,

где R – сопротивление цепи гальванометра.

Если магнитный поток изменяется на величину , то можно найти заряд, протекший через индукционную катушку:

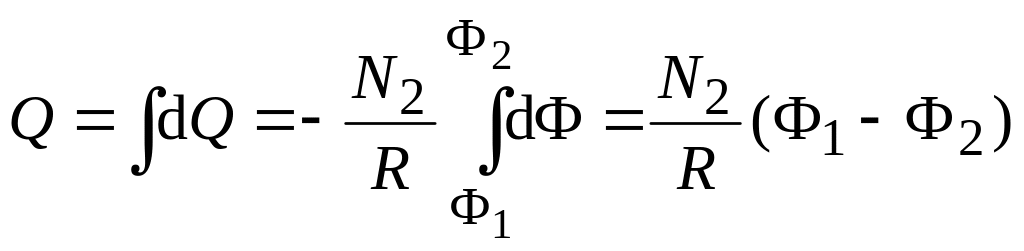(3.9)

Количество протекшего электричества определяется по отбросу светового указателя баллистического гальванометра: Q=βm, где m – число делений по шкале гальванометра; β – постоянная гальванометра.

Если изменение потока индукции от Ф₁ до Ф₂ происходит при изменении тока в катушке I от какого-то значения I до – I, то Ф₁=ВS,

Ф₂ =−BS.

,

где B – значение индукции поля, соответствующего тока;

S – площадь поперечного сечения сердечника.

Учтя всё сказанное, можно придать формуле (3.9) следующий вид:

.

Из полученного выражения нетрудно определить В:

(3.10)

Все величины, стоящие перед m в правой части равенства, постоянны для данной установки, совокупность их можно обозначить через С₀ ( ). Формула (3.10) примет теперь более простой вид:

(3.11)

Таким образом, для снятия кривой намагничивания надо производить переключения тока в намагничивающей катушке I при различных значениях I и измерять отбросы светового указателя баллистического гальванометра m. По значениям I определяется, согласно формуле (3.6), величина H; по значениям отбросов m – соответствующая величина B, согласно формуле (3.11).

Кривая намагничивания строится в координатах B H (H – на оси абсцисс, B – на оси ординат). По полученной кривой намагничивания можно определить магнитную проницаемость μ и построить график функции μ=f(H).