Задача 58.

Страховщик заключил договор имущественного страхования сроком на 1 год, по условиям которого страховая премия вносится страхователем по частям (равными долями, ежеквартально) на расчетный счет страховщика в коммерческом банке (КБ). Условия договора страхования и начисления процентов банком указаны в таблице 39. Определить величину суммы на расчетном счете страховщика по истечении срока договора страхования, если номинальная процентная ставка КБ составляет 12 % годовых.

Таблица 39 Исходные данные

Наименование	Вариант
Наименование	А	Б	В	Г
Страховая сумма, тыс.руб.	500	600	700	800
Страховой тариф-брутто, %	9,5	8,5	10,5	11,5
Начисление процентов в КБ в течение года (проценты сложные, в году 365 дней)	по полугодиям	по кварталам	ежемесячно	ежедневно

Список литературы

Александров А.А. Страхование. М.: ПРИОР, 1998.- 192 с.
Ван Хорн Дж.К. Основы управления финансами: Пер. с англ./ Гл.ред. Я.В.Соколов.- М.: Финансы и статистика, 1996.
Воблый К.Г. Основы экономики страхования.- М.: АНКИЛ, 1995.- 228 с.
Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб.пособие для вузов. Изд. 7-е, стер.- М.: Высш.шк., 1999.- 479 с.
Гражданский кодекс Российской Федерации. ч. I, II.
Колемаев В.А. Математическая экономика: Учебник для вузов.- М.: ЮНИТИ, 1998.- 240 с.
Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие.- М.: ИНФРА-М, 1997.- 208 с.
Методика оценки остаточной стоимости транспортных средств с учетом технического состояния, НИИАТ, утв. Министерством транспорта Российской Федерации 10.12.1998 г., рег. номер Р-03112194-0376-98.
Методики расчета тарифных ставок по рисковым видам страхования. Утв.распоряжением Росстрахнадзора от 08.07.93 г. № 02-03-36.
Основы страховой деятельности: Учебник/ Отв.ред.проф.Т.А.Федорова.- М.: БЕК, 1999.- 776 с.
Саркисов С.Э. Личное страхование.- М.: Финансы и статистика, 1996.- 96 с.
Страховое дело: Учебник/ Под ред.проф. Л.И.Рейтмана.- М.: Банковский и биржевой научно-консультационный центр, 1992.- 524 с.
ФЗ РФ в редакции от 25.02.99 г. "О медицинском страховании граждан в РФ".
ФЗ РФ в редакции от 31.12.97 г. "Об организации страхового дела в РФ".
ФЗ РФ от 29.07.98 г. "Об оценочной деятельности в РФ"
Хорин А.Н. "Раскрытие существенной информации в бухгалтерской отчетности", Бухгалтерский учет, № 9-12, 1999.
Шахов В.В. Введение в страхование: Учебное пособие.- 2-е изд., перераб. и доп.- М.: Финансы и статистика, 1999.- 288 с.
Amir D. Aczel. Complete Business Statistics "Bentley college, 1989. Boston, USA - 1056 p.

ПРИЛОЖЕНИЯ

Приложение А

Основные сведения из теории вероятностей, применяемые в страховании

Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления:

Для несовместных событий А, В:

Сумма вероятностей событий А₁, А₂, А₃ … А_n образующих полную группу, равна 1:

События А и В называются независимыми, если вероятность каждого из них не зависит от того, произошло или нет другое событие.

События А и В называются зависимыми, если вероятность каждого из них зависит от того, произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось. называется условной вероятностью: Р(В/А).

Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:

Формула полной вероятности:

где Н₁, Н₂ … Н_n - попарно несовместные события (гипотезы).

Формула Байеса:

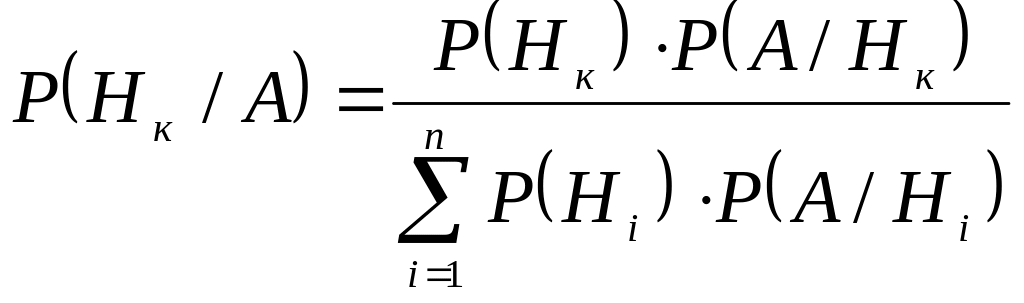, к= 1, 2 … n.

Вероятности Р(Н_к) событий Н₁, Н₂ … Н_n до опыта называются априорными ( от латинского a priori, что означает "сперва", т.е. до того, как был произведен опыт). Вероятности Р(Н_к/ А) тех же событий называются апостериорными, т.е. после проведения опыта.

Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Биномиальное распределение.

В одинаковых условиях производится n независимых опытов, в каждом из которых может появиться событие А с вероятностью р или событие с вероятностью q (q=1-p). Вероятность того, что при n опытах событие А появится k_раз и не появится n-k_раз определяется формулой Бернулли:

Биномиальный ^* закон распределения дискретной случайной величины X (Х - это число появлений события А при n опытах)

Х	0	1	…	k	…	n
p			…		…	pⁿ

Распределение Пуассона является предельным случаем биномиального распределения, когда n является достаточно большим, а р - достаточно малым (т.е. речь идет о довольно редких появлениях события А).

Рапределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой: