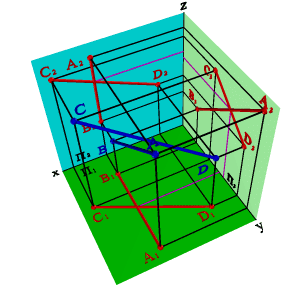
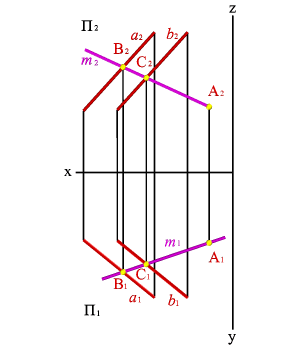
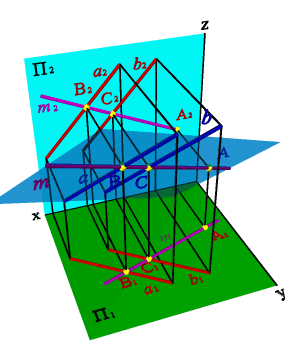
2. Пересекающиеся прямые.

Пересекающимисяназываются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи(рис. 3.21).

а) модель		б) эпюр
Рисунок 3.21. Пересекающиеся прямые

В общем случае справедливо и обратное утверждение, но есть два частных случая:

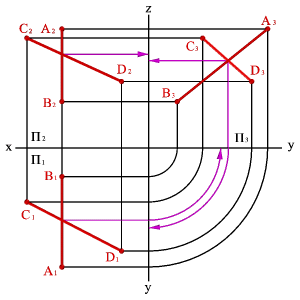
1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например профильной плоскости проекций (рис. 3.22), по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВиСДпересекаются, причем точка пересечения проекций лежит на одной линии связи, профильные проекции этих отрезков тоже пересекаются, однако точка их пересечения не лежит на одной линии связи с точками пересечения горизонтальной и фронтальной проекций отрезков, следовательно, не пересекаются и сами отрезки.

а) модель		б) эпюр
Рисунок 3.22.Одна из прямых параллельна профильной плоскости проекций

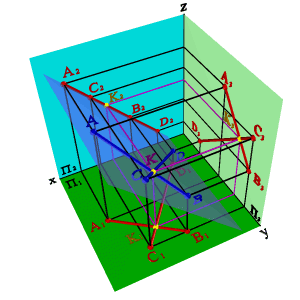
2. Пересекающие прямые расположены в общей для них проекционной плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 3.23). О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной проекции, например, на горизонтальную плоскость проекций (А₁В₁∩С₁D₁ÞАВ∩СD)

а) модель		б) эпюр
Рисунок  3.23. Пересекающиеся прямые расположены в фронтально проецирующей плоскости

3. Скрещивающиеся прямые

Скрещивающимисяназываются две прямые не лежащие в одной плоскости.

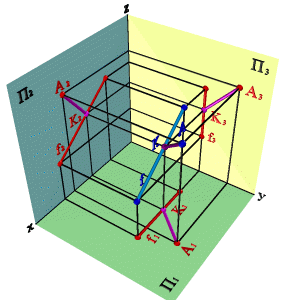
Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

Точке пересечения фронтальных проекций прямых (рис. 3.24) соответствуют две точки АиВ, из которых одна принадлежит прямойа,другаяв . Их фронтальные проекции совпадают лишь потому, что в пространстве обе точкиАиВнаходятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точкаВлежащая на прямойв, следовательно, прямаяв проходит в этом месте ближе прямойаи фронтальная проекция точкиВзакрывает проекцию точкиА. (Для точекСиДрешение аналогично).

Этот способ определения видимости по конкурентным точкам. В данном случае  точкиАиВ- фронтально конкурирующие, а С и Д -горизонтально конкурирующие.

а) модель		б) эпюр
Рисунок 3.24. Скрещивающиеся прямые

Лекция №3-6 Проекции плоских углов.

 

 

Угол- геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.Углом между прямыми называется меньший из двух углов между лучами, параллельными этим прямым.Углом между плоскостью и не перпендикулярной ей прямой называется угол между прямой и её проекцией на данную плоскость.

Рассмотрим ряд свойств ортогональных проекций плоских углов:

1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения (Теорема о проецировании прямого угла)

Рисунок 3.25. Теорема о проецировании прямого угла	Рисунок 3.26. Обратная теорема о проецировании прямого угла

_{Дано: ÐАВС = 90}^о_{; [ВС] // П1; [АС] # П1.}

_{Для доказательства теоремы продлим отрезок АС до пересечения с плоскостью П1 (рис. 3.25) получим горизонтальный след прямой - точку М º М1, одновременно принадлежащую прямой и ее проекции. Из свойства ортогонального проецирования следует, что [ВС] // [В1С1]. Если через точку М проведем прямую МD параллельную С1В1 , то она будет параллельна и СВ, а следовательно ÐСМD= 90}^о_{. Согласно теореме о трех перпендикулярах ÐС1МD=90}^о_.Таким образом,MDА₁С₁ иMD//В₁С₁, следовательно,А₁С₁В₁ 90^о, что и требовалось доказать. _{В случае когда [АС^]П1 проекцией угла, согласно свойствам ортогонального проецирования, будет прямая линия.}

_{2. Если проекция угла представляет угол 90}⁰_{, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций (рис. 3.26).}

3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу. 

_{4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.}

5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением.

Лекция №4   

 

типы задач начертательной геометрии

Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. В связи с этим все многообразие задач может быть отнесено к двум группам:

1.Задачи позиционные– решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов (в частном случае, выяснить их взаимную принадлежность) как по отношению друг к другу, так и относительно системы координатных плоскостей проекций.

2.Задачи метрические– при решении задач этой группы появляется возможность ответить на вопросы, касающиеся как внутренней метрики заданных геометрических объектов (определение расстояния между различными точками объекта и нахождения углов между линиями и поверхностями, принадлежащими этому объекту), так и определение расстояний между точками и величин углов между линиями и поверхностями, принадлежащими различным объектам.

В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений при этом определяются не только сложностью задачи, но и в значительной степени зависит от того, с какими проекциями (удобными или неудобными) приходится иметь дело. При этом наиболее выгодным частным положением геометрического объекта следует считать:

 Положение, перпендикулярноек плоскости проекций (для решения позиционных, а в ряде случаев, и метрических задач);

  Положение, параллельноепо отношению к плоскости проекций (при решении метрических задач).

При решении метрических задач, связанных с определением истинных размеров изображенных на эпюре фигур, могут встретиться значительные трудности, если заданные проекции не подвергнуть специальным преобразованиям.

Рассмотрим на примере: Определить расстояние от точкиАдо прямойm. Расстояние от точки до прямой - это натуральная величина перпендикуляра восстановленного из точки к прямой линии. Простейшим условием такой задачи является случай, когда прямая является проецирующей. Определим расстояние от точкиАдо прямойm, когда прямая является горизонтально проецирующей линией (рис. 4.1), т.е.m^П₁, m \\ П₂, m \\ П₃. Согласно, теореме о проецировании прямого угла, перпендикуляр из проекций точкиАможно проводить к фронтальной и профильной проекции прямойm, при этом полученный отрезокАК- горизонталь, т.е. параллелен горизонтальной плоскости проекций и на эту плоскость проецируется в натуральную величину.

а) модель		б) эпюр
Рисунок 4.1. Расстояние от точки до горизонтально проецирующей прямой

Методы преобразования ортогональных проекций

 Если прямая параллельна одной из плоскостей проекций т.е. является прямой уровня, то без преобразования ортогональных проекций можно только найти проекции перпендикуляра. Пусть прямая  f фронталь, т.е.f \\ П₂значит перпендикуляр можно проводить из проекцийА₂к фронтальной  проекции прямойm₂, на эту плоскость угол будет проецироваться без искажения (рис. 4.2). Однако полученные проекции отрезкаАК не отражают истинной величины отрезка потому, чтоАК - отрезок прямой общего положения.

а) модель		б) эпюр
Рисунок 4.2. Расстояние от точки до фронтальной прямой

Общий случай подобной задачи, когда требуется найти расстояние от точки до прямой общего положения, то даже построение проекции искомого отрезка без преобразования проекций не представляется возможным.

Сопоставление приведенных чертежей показывает, что трудности решения одной и той же задачи существенно зависят от положения геометрических объектов относительно плоскостей проекций.

В связи с этим, естественно, возникает вопрос, каким путем можно получить удобные проекции для решения поставленной задачи по заданным неудобным ортогональным проекциям.

Переход от общего положения геометрической фигуры к частному можно осуществлять за счет изменения взаимного положения проецируемой фигуры и плоскостей проекций.

При ортогональном проецировании это достигается двумя путями:

1. Перемещение в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве - метод плоскопараллельного перемещения.

2. Перемещением плоскостей проекций в новое положение по отношению, к которому проецируемая фигура (которая не меняет положения в пространстве) окажется в частном положении - метод замены плоскостей проекций.

Лекция №4   

 

Метод плоскопараллельного перемещения

Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 4.3). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

а)модель		б) эпюр
Рисунок 4.3. Определение натуральной величины отрезка методом плоскопараллельного перемещения

Свойства плоскопараллельного перемещения:

1. При всяком перемещении точек в плоскости параллельной плоскости П₁, её фронтальная проекция перемещается по прямой линии, параллельной осих.

2. В случае произвольного перемещения точки в плоскости параллельной П₂, её горизонтальная проекция перемещается по прямой параллельной осих.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой линии - определяющей траекторию перемещения точек, метод плоскопараллельного проецирования имеет следующие частные случаи:

1. Метод вращения вокруг оси, перпендикулярной плоскости проекций;

2.  Метод вращения вокруг оси, параллельной плоскости проекций;

3. Метод вращения вокруг оси, принадлежащей плоскости проекций (вращение вокруг следа плоскости)- способ совмещения.

Рассмотрим некоторые из этих способов.

Метод вращения вокруг оси перпендикулярной  плоскости проекций

Плоскости носитель траекторий перемещения точек параллельны плоскости проекций. Траектория - дуга окружности, центр которой находится на оси перпендикулярной плоскости проекций. Для определения натуральной величины отрезка прямой общего положения АВ(рис. 4.4), выберем ось вращения перпендикулярную горизонтальной плоскости проекций и проходящую черезВ₁. Повернем отрезок так, чтобы он стал параллелен фронтальной плоскости проекций (горизонтальная проекция отрезка параллельна осиx). При этом точкаА₁переместиться вА*₁, а точкаВне изменит своего положения. Положение точкиА*₂находится на пересечении фронтальной проекции траектории перемещения точкиА(прямая линия параллельная осиx) и линии связи проведенной изА*₁. Полученная проекцияВ₂ А*₂определяет действительные размеры самого отрезка.

а) модель		б) эпюр
Рисунок 4.4. Определение натуральной величины отрезка методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций

Метод вращения вокруг оси параллельной  плоскости проекций

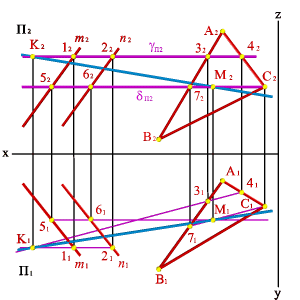
Рассмотрим этот способ на примере определения угла между пересекающимися прямыми (рис.4.5). Рассмотрим две проекции пересекающихся прямых а ив которые пересекаются в точкеК. Для то чтобы определить натуральную величину угла между этими прямыми необходимо произвести преобразование ортогональных проекций так, чтобы прямые стали параллельны плоскости проекций. Воспользуемся способом вращения вокруг линии уровня - горизонтали. Проведем произвольно фронтальную проекцию горизонталиh₂параллельно осиОх, которая пересекает прямые в точкахА₂иВ₂. Определив проекцииА₁иВ₁, построим горизонтальную проекцию горизонталиh₁ . Траектория движения всех точек при вращении вокруг горизонтали - окружность, которая проецируется на плоскость П₁ в виде прямой линии перпендикулярной горизонтальной проекции горизонтали.

	а) модель		б) эпюр
Рисунок 4.5. Определение угла между пересекающимися прямыми, вращением вокруг оси параллельной горизонтальной плоскости проекций

Таким образом, траектория движения точки К₁определена прямойК₁О₁, точкаО-центр окружности - траектории движения точкиК. Чтобы найти радиус этой окружности найдем методом треугольника натуральную величину отрезкаКО.Продолжим прямуюК₁О₁так чтобы|КО|=|О₁К*₁| . Точка К*₁ соответствует точке К , когда прямые а и в лежат в плоскости параллельной П₁ и проведенной через горизонталь - ось вращения. С учетом этого через точку К*₁ и точки А₁ и В₁ проведем прямые, которые лежат теперь в плоскости параллельной П₁, а следовательно и угол j - натуральная величина угла между прямыми а и в.

Метод замены плоскостей проекций

Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П₁иП₂новыми плоскостямиП₄(рис. 4.6). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 4.7). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Задача 1: Определить натуральную величину отрезка АВпрямой общего положений (рис. 4.6). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.

Выберем новую плоскость проекций П₄, параллельно отрезкуАВи перпендикулярно плоскостиП₁. Введением новой плоскости, переходим из системы плоскостейП₁П₂в системуП₁П₄, причем в новой системе плоскостей проекция отрезкаА₄ В₄будет натуральной величиной отрезкаАВ.

	а) модель		б) эпюр
Рисунок 4.6. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

Задача 2: Определить расстояние от точки Адо прямой общего положения, заданной отрезкомАВ(рис._4.7).

	а) модель		б)эпюр
Рисунок 4.7. Определение расстояния от точки до прямой общего положения методом замены плоскостей проекций

Лекция №5-1

 

Плоскость

Плоскость– одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости:

1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;

2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.

Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Общее уравнение плоскости:

Ax+By+Cz+D=0,

где А, В, С, иD- постоянные, причемА, ВиСодновременно не равны нулю.

 

Способы графического задания плоскостей

Положение плоскости в пространстве можно определить:

1. Тремя точками, не лежащими на одной прямой линии (рис.5.1);

а) модель		б) эпюр
Рисунок 5.1. Плоскость заданная тремя точками, не лежащими на одной прямой

2. Прямой линией и точкой, не принадлежащей этой прямой (рис.5.2);

а) модель		б) эпюр
Рисунок 5.2. Плоскость заданная прямой линией и точкой, не принадлежащей этой линии

3. Двумя пересекающимися прямыми (рис.5.3);

а) модель		б) эпюр
Рисунок 5.3. Плоскость заданная двумя пересекающимися прямыми линиями

4. Двумя параллельными прямыми (рис.5.4);

а) модель		б) эпюр
Рисунок 5.4. Плоскость заданная двумя параллельными прямыми линиями

Лекция №5-2

 

Различное положение плоскости относительно  плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения.  Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальныйa_П1; - фронтальныйa_П2; - профильныйa_П3).

Следы плоскости общего положения пересекаются попарно на осях в точках a_x,a_y,a_z. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях (рис.5.5).

2.Плоскости перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2.1. Плоскость перпендикулярная горизонтальной плоскости проекций (^aP₁), называетсягоризонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек любых фигур в этой плоскости совпадают с горизонтальным следом (рис.5.6).

а) модель		б) эпюр
Рисунок 5.6. Горизонтально проецирующая плоскость

2.2. Плоскость перпендикулярная фронтальной плоскости проекций (a^П₂)-фронтально проецирующая плоскость. Фронтальной проекцией плоскостиaявляется прямая линия, совпадающая со следомa_П2(рис.5.7).

а)модель		б) эпюр
Рисунок 5.7. Фронтально проецирующая плоскость

2.3. Плоскость перпендикулярная профильной плоскости ( ^aП₃) -профильно проецирующая плоскость. Частным случаем такой плоскости являетсябиссекторная плоскость(рис.5.8).

а) модель		б) эпюр
Рисунок 5.8. Биссекторная плоскость

3. Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называютсяплоскостями уровня.В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:

3.1. Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (a//П₁) -  (^aП₂,^aП₃). Любая фигура в этой плоскости проецируется на плоскостьП₁без искажения, а на плоскостиП₂иП₃в прямые - следы плоскостиa_П2иa_П3(рис.5.9).

а) модель		б) эпюр
Рисунок 5.9. Горизонтальная плоскость

3.2. Ф^{ронтальная плоскость - плоскость параллельная фронтальной плоскости проекций (}a^//П₂^{), (}a^{^П}₁^, a^{^П}₃^). Любая фигура в этой плоскости проецируется на плоскостьП₂без искажения, а на плоскостиП₁иП₃в прямые - следы плоскостиa_П1иa_П3(рис.5.10).

а) модель		б) эпюр
Рисунок 5.10. Фронтальная плоскость

3.3^. П^{рофильная плоскость - плоскость параллельная профильной плоскости проекций (}a^//П₃^{), (}a^{^П}₁^, a^{^П}₂^). Любая фигура в этой плоскости проецируется на плоскостьП₃без искажения, а на плоскостиП₁иП₂в прямые - следы плоскостиa_П1иa_П2(рис.5.11).

а) модель		б) эпюр
Рисунок 5.11. Профильная плоскость

Лекция №5-3

 

Следы плоскости

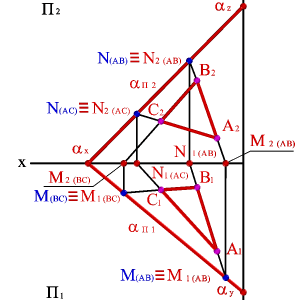
Следом плоскостиназывается линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают:горизонтальный,фронтальныйипрофильныйследы плоскости.

^{Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой( как для построения любой прямой). На рисунке 5.12 показано нахождение следов плоскости α(АВС). Фронтальный след плоскости α}_П2^{, построен, как прямая соединяющая две точки N}_(АС) ^{и N}_(АВ)^{, являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α.Горизонтальный след α}_П1 ^{– прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след α}_П3 ^{– прямая соединяющая точки (α}_y ^{и α}_z^{) пересечения горизонтального и фронтального следов с осями.}

	а) модель		б) эпюр
Рисунок 5.12. Построение следов плоскости

Взаимное расположение прямой и плоскости

Определение взаимного положения прямой и плоскости - позиционная задача, для  решения которой применяетсяметод вспомогательных секущих плоскостей. Сущность метода заключается  в следующем: через прямую проведем вспомогательную секущую плоскостьg и установим относительное положение двух прямыхаив, последняя из которых является линией пересечения вспомогательной секущей плоскостиgи данной  плоскостиa(рис.5.13).

Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая алежит в плоскостиa,параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю когда прямаяапересекает плоскостьa. Таким образом возможны три случая относительного расположения прямой и плоскости: Прямая принадлежит плоскости; Прямая параллельна плоскости; Прямая пересекает плоскость, частный случай – прямая перпендикулярна плоскости. Рассмотрим каждый случай.

Рисунок 5.13. Метод вспомогательных секущих плоскостей

Прямая линия, принадлежащая плоскости

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат той же плоскости (рис.5.14).

Задача. Дана плоскость (n,k) и одна проекция прямой m₂.

Требуется найти недостающие проекции прямой mесли известно, что она принадлежит плоскости, заданной пересекающимися прямымиnиk.

Проекция прямой m₂пересекает прямыеnиkв точкахВ₂иС₂, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек ВиСкак точек лежащих на прямых соответственноnиk.

Таким образом точки ВиСпринадлежат плоскости заданной пересекающимися прямымиnиk, а прямаяmпроходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.

			а) модель		б) эпюр
Рисунок 5.14. Прямая и плоскость имеют две общие точки

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.5.15).

Задача.

Через точку Впровести прямуюmесли известно, что она принадлежит плоскости заданной пересекающимися прямымиnиk.

Пусть В принадлежит прямойn лежащей в плоскости заданной пересекающимися прямымиnиk. Через проекциюВ₂проведем проекцию прямойm₂параллельно прямойk₂, для нахождения недостающих проекций прямой необходимо построить проекцию точки В₁,как точки лежащей на проекции прямойn₁и через неё провести проекцию прямойm₁параллельно проекцииk₁.

Таким образом точки Впринадлежат плоскости заданной пересекающимися прямымиnиk, а прямаяmпроходит через эту точку и параллельна прямойk, значит согласно аксиоме прямая принадлежит этой плоскости.

	а) модель		б) эпюр
Рисунок 5.15. Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости

Главные линии в плоскости

Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:

1. Горизонтали h- прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций(hÎСВА, h//P₁, h₂//Ох,h₃//Оy)(рис.5.16).

	а) модель		б) эпюр
Рисунок 5.16. Горизонталь

2. Фронталиf- прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций(fÎСВА, f//P₂, f₁//Ох, f₃//Оz)(рис.5.17).

	а) модель		б) эпюр
Рисунок 5.17. Фронталь

3. Профильные прямыер- прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций(рÎСВА, р//P₃, р₁^Ох, р₂^Ох) (рис.5.18).

	а) модель		б) эпюр
Рисунок 5.18. Профильная прямая

Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

4. Линия наибольшего скатаи её горизонтальная проекция образуют линейный уголj, которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.5.19).

	а) модель		б) эпюр
Рисунок 5.19. Линия наибольшего ската

Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее. 

Прямая линия, параллельная плоскости

При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскостии не принадлежит этой плоскости.

Задача.Дано: проекции плоскости общего положенияABCи прямой общего положенияа.

Требуется оценить их взаимное положение (рис.5.20). 

	а) модель		б) эпюр
Рисунок 5.20. Прямая параллельная плоскости

Для этого через прямую апроведем вспомогательную секущую плоскостьg- в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей gиАВС- прямуюп(DF). Проекция прямойпна горизонтальную плоскость проекций совпадает с проекциейа₁и со следом плоскостиg. Проекция прямойп₂параллельнаа₂, п₃параллельнаа₃, следовательно, прямаяапараллельна плоскостиAВС.

 

Прямая линия, пересекающая плоскость

Нахождение точки пересечения прямой линии и плоскости – основная задача начертательной геометрии.

Задача. Дано: плоскостьAВС и прямаяа.

Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.

Для решения задачи:

1. Через горизонтальную проекцию прямой а₁проведем вспомогательную горизонтально проецирующую плоскостьg(таким образом а g Î).

2. Горизонтальный след плоскости g₁пересекает проекцию плоскостиA₁В₁С₁в точкахD₁ иF₁, которые определяют положение горизонтальной проекциип₁- линии пересечения плоскостейgиAВС. Для нахождения фронтальной  и профильной проекциипспроецируем точкиDиFна фронтальную  и профильную плоскости проекций.

3. На фронтальной и профильной проекциях линия пересечения плоскостей ппересекает  проекцииав точкеК, которая и является  проекцией точки пересечения прямойас плоскостью AВС, по линии связи находим горизонтальную проекциюК₁.

4. Методом конкурирующих точек определяем видимость прямой апо отношению к плоскостиAВС.

	а) модель		б) эпюр
Рисунок 5.21. Нахождение точки пересечения прямой и плоскости

Таким образом алгоритм решения задачи состоит из следующей последовательности действий (рис.5.21):

1. Построение вспомогательной секущей плоскости g (горизонтально – проецирующая плоскость ), которую проводят через прямуюа (а)gÎ;

2. Построение линии пересечения вспомогательной плоскости gи заданной плоскостиa (п)gÇa=;

3. Определение искомой точки К, как точки пересечения двух прямых, заданной -аи полученной в результате пересечения плоскостей –п (К=а Ç п). В качестве вспомогательной плоскостиgрекомендуется брать одну из проецирующих плоскостей.

4. Определение видимости прямой а относительно плоскостиa.

Прямая линия перпендикулярная плоскости.

Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Пусть прямая n, перпендикулярная плоскости,пересекает плоскостьBCDв точкеN, тогда по условиюn перпендикулярна любой прямой плоскости. Проведем в плоскостиBCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е.n₁ h₁. Аналогично для фронтали –f n f₂  n₂.

Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.

Доказательство следует из теоремы о проецировании прямого угла.

Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А(рис.5.22).

Задача. Дано: плоскостьВСD и точкаА.

Требуется построить прямую линиюnпроходящую через точкуАи перпендикулярную плоскостиВСD.

В плоскости ВСDпостроим фронтальfи горизонтальh. В горизонтальной плоскости проекций проведем через точкуА₁прямуюn₁перпендикулярно горизонтальной проекции горизонталиh₁, а на фронтальной плоскости проекций через точкуА₂прямуюn₂перпендикулярно фронтальной проекции фронталиf₂, согласно выше сказанному полученная прямаяnбудет перпендикулярна плоскостиВСD.

	а) модель		б) эпюр
Рисунок 5.22. Построение прямой, перпендикулярной плоскости

Взаимное расположение точки и плоскости

Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.

Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.

Рассмотрим пример (рис.5.23): Построение проекции точки Апринадлежащей плоскости общего положения заданной двумя параллельными прямымиa(a//b).

Задача. Дано: плоскость(а,в) и  проекция точкиА₂.

Требуется построить проекциюА₁если известно, что точкаАлежит в плоскостив,а.

 Через точку А₂ проведем проекцию прямойm₂, пересекающую проекции прямыхa₂ иb₂в точкахС₂иВ₂(С,aÎ BaÎ Þ maÎ).Построив проекции точекС₁иВ₁, определяющие положениеm₁, находим горизонтальную проекцию точкиА(А₁Î m₁, maÎ Þ АaÎ).

 

	а) модель		б) эпюр
Рисунок 5.23. Точка,принадлежащая плоскости

 

Через точку А₂ проведем проекцию прямойm₂, пересекающую проекции прямыхa₂ иb₂в точкахС₂иВ₂(СÎ,aBÞaÎmaÎ).Построив проекции точекС₁иВ₁, определяющие положениеm₁, находим горизонтальную проекцию точкиА(А₁Î m₁, m ÞaÎ АaÎ).

 

Лекция №5_5

 

Взаимное расположение точки и плоскости

Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.

Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.

Рассмотрим пример (рис.5.23): Построение проекции точки Апринадлежащей плоскости общего положения заданной двумя параллельными прямымиa(a//b).

Задача. Дано: плоскость(а,в) и  проекция точкиА₂.

Требуется построить проекциюА₁если известно, что точкаАлежит в плоскостив,а.

 Через точку А₂ проведем проекцию прямойm₂, пересекающую проекции прямыхa₂ иb₂в точкахС₂иВ₂(С,aÎ BaÎ Þ maÎ).Построив проекции точекС₁иВ₁, определяющие положениеm₁, находим горизонтальную проекцию точкиА(А₁Î m₁, maÎ Þ АaÎ).

 

	а) модель		б) эпюр
Рисунок 5.23. Точка,принадлежащая плоскости

Через точку А₂ проведем проекцию прямойm₂, пересекающую проекции прямыхa₂ иb₂в точкахС₂иВ₂(СÎ,aBÞaÎmaÎ).Построив проекции точекС₁иВ₁, определяющие положениеm₁, находим горизонтальную проекцию точкиА(А₁Î m₁, m ÞaÎ АaÎ).

 

Взаимное расположение двух плоскостей

Две плоскости в пространстве могут быть либо взаимно параллельны, в частном случае совпадая друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.

1.Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Это определение хорошо иллюстрируется задачей, через точку Впровести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми ab(рис.5.24).

Задача.Дано: плоскость общего положения, заданную двумя пересекающимися прямымиabи точкаВ.

Требуется через точку Впровести плоскость, параллельную плоскостиab и задать её двумя пересекающимися прямымиc иd.

Согласно определения если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости то эти плоскости параллельны между собой.

Для того чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой

d//a,с//b  Þ d₁//a₁,с₁//b₁;d₂//a₂,с₂//b₂;d₃//a₃,с₃//b₃.

	а) модель		б) эпюр
Рисунок 5.24. Параллельные плоскости

2.Пересекающиеся плоскости, частный случай – взаимно перпендикулярные плоскости. Линия пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

Рассмотрим построение линии пересечения двух плоскостей, когда одна из них проецирующая (рис.5.25).

Задача. Дано: плоскость общего положения задана треугольникомАВС, а вторая плоскость - горизонтально проецирующаяa.

Требуется построить линию пересечения плоскостей.

Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВСможно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостьюa- точкаD, прямой (AС) -F. Отрезок[DF]определяет линию пересечения плоскостей. Так как- горизонтально проецирующая плоскость, то проекцияD₁F₁совпадает со следом плоскости_П1 таким образом остается только построить недостающие проекцииDFнаП₂иП₃.

	а) модель		б) эпюр
Рисунок 6.25. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью

Перейдем к общему случаю. Пусть в пространстве заданы две плоскости общего положения a(n,m)иb(ABC) (рис.5.26).

	а) модель		б) эпюр
Рисунок 5.26. Пересечение плоскостей общего положения

 

Рассмотрим последовательность построения линии пересечения плоскостей a(m//n)иb(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскостиgиd. Найдем линии пересечения этих плоскостей с рассматриваемыми плоскостями. Плоскостьgпересекает плоскостьaпо прямой (12), а плоскостьb- по прямой (34). ТочкаК- точка пересечения этих прямых одновременно принадлежит трем плоскостямa, bиg, являясь таким образом точкой принадлежащей линии пересечения плоскостейaиb. Плоскостьdпересекает плоскостиaиbпо прямым (56) и (7C) соответственно, точка их пересеченияМрасположена одновременно в трех плоскостяхa, b, dи принадлежит прямой линии пересечения плоскостейaиb. Таким образом найдены две точки принадлежащие линии пересечения плоскостейaиb- прямая (КМ).

Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость.

Взаимно перпендикулярные плоскости. Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точкуАможно провести множество плоскостей перпендикулярных данной плоскостиa(f,h). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точкиАна плоскостьa. Для того чтобы из точкиАпровести плоскость перпендикулярную плоскости заданной двумя пересекающимися прямымиhf необходимо из точкиАпровести прямую n перпендикулярную плоскостиhf(горизонтальная проекция nперпендикулярна горизонтальной проекции горизонталиh, фронтальная проекцияnперпендикулярна фронтальной проекции фронталиf). Любая плоскость проходящая через прямуюnбудет перпендикулярна плоскостиhf, поэтому для задания плоскости через точки Апроводим произвольную прямуюm. Плоскость заданная двумя пересекающимися прямымиmnбудет перпендикулярна плоскостиhf (рис.5.27).

а) модель		б) эпюр
Рисунок 5.27. Взаимно перпендикулярные плоскости

Лекция №6-1