8. Эконометрическая модель – система одновременных уравнений

Как уже отмечалось, основу эконометрической модели составляет система регрессионных уравнений, каждое из которых отображает одну из зависимостей, закономерностей изменения, свойств изучаемого сложного объекта. Помимо регрессий в модель могут быть включены выражения, описывающие тренды развития отдельных явлений, и тождества, характеризующие балансовые увязки между переменными, или уравнения, увязывающие между собой отдельные характеристики модели во времени (динамический вариант модели).

Эконометрическая модель содержит так называемые эндогенные и экзогенные переменные. Эндогенными переменными являются те, значения которых выясняются на основе модели. Экзогенные переменные определяются вне модели. Эндогенные и экзогенные переменные могут быть также лаговыми. Под лаговой переменной понимают переменную, значения которой отстают на один или несколько периодов (если X_{2 t} - значения обычной переменной, то X_{2, t-1} - ее лаговые значения, смещенные на один период). Лаговые и экзогенные переменные образуют множество предопределенных переменных. Совместно зависимыми переменными называются обычные эндогенные переменные, которые объясняются эконометрической моделью в момент времени t.

Модель содержит также различного рода параметры (коэффициенты), которые определяются в ходе статистического оценивания путем обработки имеющейся информации (данных наблюдения).

При разработке системы регрессионных уравнений часто оказывается, что зависимые переменные одних уравнений выступают в качестве независимых переменных других. Такие модели (или отдельные уравнения) называются взаимозависимыми (или одновременными). Взаимозависимые модели имеют две формы: структурную и приведенную. Структурная форма модели создается в процессе формирования самой модели при стремлении отразить причинно-следственный механизм, существующий в реальности. Она позволяет проследить влияние изменений экзогенных переменных модели на значения эндогенных переменных. Параметры уравнений модели в данной форме получили название структурных коэффициентов. Использование обычного метода наименьших квадратов для оценивания структурных уравнений , каждого в отдельности, приведет в общем случае к получению смещенных и несостоятельных оценок.

По предположению система уравнений структурной формы модели должна быть совместной и, следовательно, она может быть решена относительно эндогенных переменных. Результат решения и представляет собой приведенную форму модели.

Пример 4. Пусть имеем следующую линейную взаимозависимую модель (систему регрессионных уравнений) в структурной форме, относящуюся к моменту времени t ,

где t = 1,2,...,n:

Y_1t = -a₁₂Y_2t + b₁₁X_1t + b₁₂X_2t + e_1t ,

Y_2t = -a₂₁Y_1t + b₂₁X_1t + b₂₃X_3t + e_2t , (14)

где Y_1t - денежное обращение;

Y_2t - оборачиваемость денег;

X_1t - фиктивная переменная при свободном члене уравнения, тождественно равная 1;

X_2t - денежные доходы населения;

X_3t - размер вклада в сберегательную кассу,

е _{i t} - остатки уравнений, являющиеся реализациями случайных составляющих модели, или возмущений.

Отрицательные коэффициенты в правых частях уравнений при переменных Y_1t и Y_2t указывают на их обратную зависимость : денежное обращение (количество денег в обороте) должно быть тем больше, чем меньше величина оборачиваемости денег.

Используя матричную форму записи, представим эту систему в следующем виде:

AY = BX + e , (15)

Где

А = , В = , Y = ,

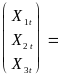
X = , e = .

Из приведенного примера видно, что не все переменные входят сразу во все уравнения.

Выражения (14) и (15) представляют собой систему одновременных уравнений. Одновременный характер модели очевиден: зависимая переменная одного уравнения выступает как объясняющая переменная в других уравнениях или объясняющие переменные в одном или нескольких уравнениях включены в другое уравнение системы как подлежащие объяснению, т.е. как зависимые. Отдельные уравнения модели не могут более рассматриваться изолированно друг от друга. К ним должны быть применены и особые приемы оценивания. Так, метод наименьших квадратов не может непосредственно применяться при оценивании параметров структурных уравнений модели из взаимозависимых переменных, поскольку оценки будут смещены и несостоятельны.

Умножив (15) слева на матрицу А^-1 ( на обратную матрицу ), получим:

А^-1 АY = А^-1ВХ + А^-1е ,

или

Y = CX + U, (16)

где U = A^-1e , C = A^-1B , (17)

или В = АС. (17).

Форма эконометрической модели, задаваемой в виде (16), называется приведенной.

Представим матричное уравнение (16) подробно (в виде отдельных уравнений):

Y_{1 t} = c₁₁X_1t + c₁₂X_2t + c₁₃X_3t + u_1t ,

Y_{2 t} = c₂₁X_1t + c₂₂X_2t + c₂₃X_3t + u_{2t .} (18)

Из (18) видно, что совместно зависимые переменные являются линейными функциями от предопределенных и возмущающих переменных, а коэффициенты (параметры приведенной формы) есть функции структурных параметров:

C = A^-1B , А^-1 = ,

С = .

Проблемы численной оценки параметров в структурной форме и возможность преобразования структурной формы в приведенную тесно связаны с понятием идентификации модели. Модель называется идентифицируемой, если регрессионные уравнения структурной формы дают однозначное выражение экономических связей. Идентифицируемость имеет очень важное значение при построении эконометрических моделей, так как из ответа на вопрос: «идентифицировано ли данное уравнение модели?» - вытекает возможность или отсутствие возможности статистически оценить параметры модели.

Необходимое условие идентифицируемости формулируется следующим образом. Обозначим общее число предопределенных переменных системы через m, количество предопределенных переменных в i -м уравнении структурной формы через m_{i ,} число эндогенных переменных модели - n, а количество эндогенных переменных в i -м структурном уравнении через n_i . Тогда необходимое условие идентифицируемости каждого уравнения системы имеет вид:

( n + m ) - ( n_i + m_i )  n - 1; (19)

это условие часто представляется иначе:

n + m - n_i - m_i  n - 1, или

m - m_i  n_i - 1, откуда m_i^*  n_i - 1 , (20)

где m_i^* - количество предопределенных переменных, исключенных из i - го уравнения системы.

Если для всех соотношений (19) (или (20)) , i = 1,2,..., n, имеет место равенство, то говорят, что система точно идентифицирована. Если хотя бы для одного уравнения выполняется строгое неравенство, то система называется сверхидентифицированной.

При точной идентифицируемости модели для оценивания параметров ее структурной формы можно применить так называемый косвенный метод наименьших квадратов, который состоит в следующем: оценив методом наименьших квадратов параметры в приведенной модели (3) и получив таким образом матрицу С, найдем матрицу А из соотношения (17).

В случае сверхидентифицируемости системы применение косвенного метода наименьших квадратов уже не ведет к однозначной оценке структурной формы, поэтому следует использовать другие методы, например, двухшаговый метод наименьших квадратов.

Если левая часть соотношений (19) или (20) меньше правой части, то имеет место недоидентифицируемость, и все методы оценивания для совместных линейных моделей теряют силу.

Выполним проверку идентифицируемости модели (14):

n = 2, n₁ = 2, n₂ = 2, m = 3, m₁ = 2, m₂ = 2;

для первого уравнения имеем: (2 + 3) - (2 + 2)  2 - 1, 1 = 1;

для второго уравнения: (2 + 3) - (2 + 2)  2 - 1, 1 = 1.

Таким образом, оба уравнения (значит, и модель в целом) точно идентифицируемы, и можно выполнить оценку параметров модели с помощью косвенного метода наименьших квадратов. Исходные данные для расчетов приведены в табл. 7.1.

Таблица 7.1.

t	Y1	Y2	X 1	X 2	X 3
1	25	10	1	1	22
2	28	11	1	4	19
3	29	9	1	3	13
4	31	7	1	5	16
5	35	8	1	6	13
6	38	6	1	6	9
7	40	4	1	8	6
8	39	2	1	8	8
9	42	1	1	9	3
10	43	2	1	10	1

Каждое уравнение приведенной формы (18) оценим методом наименьших квадратов, в соответствии с которым коэффициенты (оценки параметров) определяются так:

С = (ХX )^-1 ХY,

где ХX = 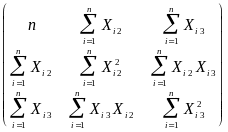, ХY = .

В первом уравнении С = , X = (X₁ X₂ X₃), Y = Y₁.

Используя данные табл. 7.1, запишем:

ХX = , ХY = .

Чтобы найти обратную матрицу ( ХX )^-1, вычислим алгебраические дополнения всех элементов исходной матрицы:

Тогда обратная матрица имеет вид:

(ХX)^-1= .

Как указано ранее, обратную матрицу можно найти с помощью функции МОБР в Excel.

Тогда матрица С =  = .

В итоге получим оценку первого уравнения в приведенной форме:

= 32,401 +1,218 X_{2 t} - 0.428 X_{3 t} . (21)

Для оценивания параметров второго уравнения вычислим:

ХY = , где Y = Y_{2 t} , и С =  = .

Имеем :

= 6,626 - 0,575 X_{2 t} + 0,257 X_{3 t} . (22)

Так как оба структурных уравнения точно идентифицируемы, параметры структурной формы однозначно определяются по параметрам приведенной формы на основе системы уравнений (см. (17)):

В = АС,

=

Из равенства матриц получим оценки:

Таким образом, структурные уравнения имеют вид:

+ 1,667 = 43,446 + 0,258 X_{2 t} , или

= -1,667 + 43,446 +0,258 X_{2 t} , (23)

0,472 + = 21,919 + 0,055 X_{3 t} ,

= -0,472 + 21,919 + 0,055 X_{3 t} . (24)

Итак, получили структурную модель:

= -1,667 + 43,446 +0,258 X_{2 t} ,

= -0,472 + 21,919 + 0,055 X_{3 t} .

По этим уравнениям мы можем сделать следующие выводы:

1. Параметры приведенной формы отражают общее воздействие предопределенных переменных на совместно зависимые переменные Y₁ и Y₂ . Так, с_{1 2} = 1,218 указывает на прямое и косвенное (возникающее на основе одновременных соотношений между Y₁ и Y₂) воздействие денежных доходов населения на денежное обращение; с_{2 3} = 0,257 указывает на непосредственное и косвенное влияние размера вклада в сберегательную кассу на оборачиваемость денег:

.

2. Параметры структурной формы отражают непосредственное воздействие факторов, отличие которого от общего воздействия становится очевидным при сравнении b₁₂ = 0,259 с c₁₂ =1,218 или b₂₃ =0,055 с c₂₃ = 0,257. Кроме того, взаимное влияние между денежным обращением и оборачиваемостью денег можно определить по параметрам а₁₂ и а₂₁ .