5.2.2. Динамически настраиваемый гироскоп с двухколечным

упругим подвесом ротора

Схема этого прецессионного ДНГ, работающего в режиме измерения угловых скоростей, представлена на рис. 5.4.

На основании 1 установлен приводной двигатель 2, на валу 3 которого с помощью внутреннего упругого карданного подвеса укреплен ротор 4. Карданный подвес составлен идентичными кольцами 5, 6, параллельно соединенными с валом и ротором упругими элементами 7, 8, 9, 10. При этом кольцо 5 соединено с валом упругим элементом 7, а с ротором – элементом 8; кольцо 6 соединено с валом упругим элементом 9, а с ротором - элементом 10. С основанием связана система координат (начало - в точке пересечения осей вала и упругих элементов, ось - ось вращения вала); с ротором связана система координат (оси расположены в экваториальной плоскости ротора и направлены по осям закрутки упругих элементов 10 и 8 соответственно). Поворот ротора относительно вала вокруг оси на малый угол осуществляется при закрутке упругих элементов 10 и 7, а поворот ротора на малый угол вокруг оси - при закрутке упругих элементов 8 и 9. При этом жесткость на изгиб упругих элементов не бесконечно велика, поскольку в силу особенностей кинематики схемы при одновременном движении ротора по углам и имеет место угол поворота ротора вокруг оси и, следовательно, изгиб упругих элементов в плоскости [5.5]. На рисунке 5.4 обозначены измерительные преобразователи 11, 12, осуществляющие измерение углов и поворота ротора относительно основания соответственно вокруг осей и , а также преобразователи моментов 13,14, обеспечивающие формирование перекрестных компенсационных моментов, воздействующих на ротор соответственно вокруг осей и . Измерительные преобразователи 11, 12 осуществляют управление преобразователями 13, 14 соответственно через блоки усиления и обработки информации 15, 16. Управляющие напряжения преобразователей моментов, являющиеся выходными напряжениями ДНГ-ДУС, обозначены .

Рассмотрим качественную картину измерения ДНГ-ДУС компонент угловой скорости основания. Будем полагать, что плоскость ротора является плоскостью динамической симметрии, и для его экваториальных главных моментов инерции справедливо соотношение . Будем полагать также, что кольца подвеса также динамически симметричны и имеет место равенство их экваториальных главных моментов инерции Ј_xk=Ј_zk. Тогда, опуская возмущающие моменты, приложенные к ротору, пренебрегая в силу малости влиянием компоненты угловой скорости вращения основания (рис. 5.4), а также изгибными деформациями упругих элементов, и учитывая малость углов и поворота ротора относительно основания, линеаризованную модель движения ротора по углам и можно представить в следующем виде [5.5]:

(Ј_x+Ј_xk )γ^״-(Ј_y+2Ј_xk)Ωδ ^׳+kγ^׳+(c-(2Ј_xk-Ј_yk)Ω²)γ-kΩδ=

(Ј_y+Ј_yk)Ωω_ζ -(Ј_x+Ј_xk)ω^׳_ζ+Μ_ДМζ+Μ_Вζ ; (5.16)

(Ј_x+Ј_xk )δ^״+(Ј_y+2Ј_xk )Ωγ^׳+ kδ^׳+ (c-(2Ј_xk-Ј_yk )Ω²)δ-kΩγ=

-(Ј_y+Ј_yk )Ωω_ζ -(Ј_x+Ј_xk )ω^׳_ζ+Μ_ДМζ+Μ_Вζ ,

где - угловая скорость вращения вала приводного двигателя; Ј_y,Ј_yk - осевые моменты инерции ротора и колец; k, c - приведенные коэффициенты момента сил вязкого трении и угловой жесткости упругих элементов на кручение; и - компенсационные и возмущающие моменты, воздействующие на ротор вокруг осей соответственно.

(5.17)

где - коэффициент усиления и передаточная функция компенсационного канала.

Отличительной особенностью уравнений (5.16) по сравнению с уравнениями (5.6) является отсутствие в правой части (5.16) гармонических членов на частоте , что определяется свойствами этого гироскопа как прецессионного гироскопа. Позиционные моменты в левой части (5.16) могут быть устранены при выполнении условия динамической настройки:

c-(2Ј_xk-Ј_yk)Ω²=0 (5.18)

Физическая суть этого условия заключается в компенсации приложенных к ротору моментов сил упругости и , создаваемых упругими элементами, соответствующими динамическими моментами сил инерции (2Ј_xk-Ј_yk)Ω²γ и (2Ј_xk-Ј_yk)Ω²δ, развиваемыми кольцами подвеса ротора. При этом гироскоп становится практически свободным. Рассмотрим этот вопрос более подробно на частном примере.

Будем полагать, что основание, на котором установлен гироскоп, не вращается (ω_ξ=ω_ζ=0), а возмущающие и компенсационные моменты отсутствуют (Μ_Вξ=Μ_Вζ=0,Μ_ДМξ=Μ_ДМζ=0). Будем полагать также, что отсутствует угол поворота ротора относительно основания вокруг оси О_ξ на угол δ (δ=0), а угол поворота вокруг оси О_ξ равен γ. На рисунке 5.5 представлена соответствующая рисунку 5.4 схема ротора ДНГ с двумя кольцами (рамками) подвеса и соединяющими их упругими элементами.

По аналогии с (5.1) имеет место соотношение:

α-jβ=(γ-jδ)e^-jΩt.

Отсюда, при δ=0 получим

α=γcosΩt, β=γsinΩt, (5.19)

где α и β – углы поворота ротора вокруг осей торсионов.

Определим сначала проекции на оси О_ξ и О_ς моментов сил упругости М_упрξ, М_упрζ, приложенных к ротору со стороны упругих элементов. Проекции этих моментов на оси x и z таковы (рис.5.5)

М_упрx=-cα, М_упрz=-cβ. (5.20)

Соответственно проекции моментов сил упругости на оси О_ξ и О_ζ имеют вид:

М_упрξ=-cαcosΩt-cβsinΩt,

М_упрζ=cαsinΩt-cβcosΩt. (5.21)

Подставляя в (5.21) соотношения (5.19), получим

М_упрξ=cγ, М_упрζ=0 (5.22)

Таким образом, дискретные упругие элементы вращающегося внутреннего карданного подвеса создают такой же М_упрξ , как если бы ротор был связан с валом сплошной упругой мембраной.

Определим теперь проекции на оси О_ξ и О_ζ моментов сил инерции М_инξ, М_инζ, приложенных к ротору со стороны колец 5,6 через связи-упругие элементы. Со стороны кольца 5 на ротор могут передаваться моменты сил инерции только по оси Ox потому, что моменты, направленные по оси Oz, парируются моментами реакции в элементах 7 (см. рис.5.4), соединяющих это кольцо с валом и обладающих практически бесконечной жесткостью на изгиб вокруг оси Oz.

Аналогично со стороны кольца 6 на ротор могут передаваться моменты сил инерции только по оси Oz.

На рисунке 5.5 с учетом малости углов α, β обозначены: Ј_xkα״ и Ј_xkβ״ – моменты сил инерции, порождаемые угловыми ускорениями колец и приложенные к ротору по осям Ox и Oz соответственно; Ωα и Ωβ – проекции угловой скорости вращения вала Ω на оси Oz и Ox соответственно; Ј_xkΩβ и Ј_xkΩα - компоненты моментов количества движения колец по осям x и z за счет Ωβ и Ωα. С учетом наличия у каждого из колец моментов количества движения также и по оси Oy, равного Ј_ykΩ, на рисунке 5.5 обозначены гироскопические моменты по оси Ox - Ј_xkΩ²α, порождаемый Ј_xkΩα и Ω, и Ј_ykΩ²α, порождаемый Ј_ykΩ и Ωα, а также гироскопические моменты по оси Oz - Ј_xkΩ²β, порождаемый Ј_xkΩβ и Ω, и Ј_ykΩ²β, порождаемый Ј_ykΩ и Ωβ.

Суммарные моменты сил инерции Минx и Минz, приложенные к ротору таковы:

М_инx= Ј_xkΩ²α­ Ј_ykΩ²α­ Ј_xkα״, (5.23)

М_инz= Ј_xkΩ²β­ Ј_ykΩ²β­ Ј_xkβ״.

Учетом (5.19) при условии постоянства угла γ, что в значительной мере справедливо для практически свободного гироскопа. (5.23) принимает вид:

М_инx= (2Ј_xk ­ Ј_yk)Ω²γcosΩt, (5.24)

М_инz= (2Ј_xk ­ Ј_yk)Ω²γsinΩt.

Проекции М_инξ, М_инζ моментов сил инерции, приложенных к ротору:

М_инξ= М_инxcosΩt+ М_инzsinΩt, (5.25)

М_инζ= М_инzcosΩt ­ М_инxsinΩt.

Из (5.25) с учетом (5.24) получим:

М_инξ=(2Ј_xk ­ Ј_yk)Ω²γ, М_инζ=0 (5.26)

Как следует из (5.26), моменты сил инерции колец подвеса, приложенные к ротору ДНГ, имеют характер позиционных моментов. Условие отсутствия упругой связи ротора с основанием – условие равенства нулю суммы моментов сил упругости (5.22) и моментов сил инерции (5.26). Оно имеет вид:

c­(2Ј_xk ­ Ј_yk)Ω²γ=0 (5.27)

и совпадает с условием динамической настройки (5.18).

Полагая, что выбором вида и параметров передаточной функции обеспечивается необходимое динамическое качество ДНГ как измерителя угловой скорости, из (5.16) с учетом (5.17), (5.18) и малости Ј_yk по сравнению с Ј_y (Ј_yk<<Ј_y) при квазипостоянных в установившемся режиме для получим:

(5.28)

где - кинетический момент гироскопа.

Тогда, имея ввиду, что K₀>>kΩ, для выходных сигналов ДНГ-ДУС имеем:

(5.29)

где - коэффициент передачи преобразователя моментов по напряжению.

Укажем теперь основные источники погрешностей ДНГ-ДУС [5.5, 5.6]. Из (5.16) непосредственно следует, что основные методические погрешности гироскопа определяются диссипативными моментами и , а также моментами сил инерции (Ј_x+Ј_xk)ω^׳_ζ , (Ј_x+Ј_xk)ω^׳_ζ , порождаемыми ускоренным вращением основания.

Инструментальные погрешности гироскопа, которые порождают смещение его нуля (дрейф) и нестабильность масштабного коэффициента, определяются динамической расстройкой (нарушение условия (5.18)) и возмущающими моментами и . Основными причинами динамической расстройки являются нестабильность , температурные и временные нестабильности угловой жесткости упругих элементов, температурные вариации моментов инерции колец Ј_xk, Ј_yk. Структуру возмущающих моментов , упрощенно можно представить следующим образом:

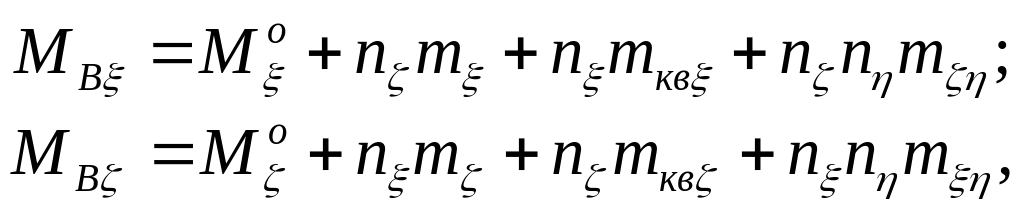(5.30)

где n_ξ ,n_η ,n_ζ - компоненты перегрузок по осям основания ; М⁰_ξ , М⁰_ζ - моменты, не зависящие от перегрузок; - удельные, отнесенные к единице перегрузки, весовые коэффициенты моментов, пропорциональных первой степени перегрузки и нормальных к ней; - удельные, отнесенные к единице перегрузки, весовые коэффициенты квадратурных моментов, пропорциональных первой степени перегрузки и коллинеарных ей; - удельные, отнесенные к произведению единичных перегрузок весовые коэффициенты моментов, пропорциональных произведению перегрузок.

Моменты, не зависящие от перегрузки, порождаются пондеромоторными силами воздействия сторонних магнитных полей на ферромагнитные элементы ротора и силами воздействия электрических полей, например, на элементы измерительных преобразователей, силами газодинамической природы, воздействующими на ротор, влиянием привода. Моменты, зависящие от первой степени перегрузки и нормальные к ней, порождаются гравиинерциальными силами при наличии смещения центра масс ротора относительно неподвижной точки подвеса. Квадратурные моменты возникают вследствие технологического несовершенства упругого подвеса, в частности вследствие непересечения его осей; моменты, пропорциональные произведению перегрузок, порождаются неравножесткостью конструкции подвеса ротора в осевом и радиальном направлениях.

Отнесенные к кинетическому моменту гироскопа моменты (5.30) определяют вариант модели дрейфов ДНГ-ДУС. Параметры этой модели в свою очередь зависят от температуры. Вариации температуры относительно номинальной порождают также изменение крутизны измерительных преобразователей углов и, что весьма существенно, крутизны преобразователей моментов.

Высокий уровень метрологических характеристик ДНГ-ДУС можно обеспечить на основе использования этой или других адекватных моделей дрейфов [5.5,5.6] путем предварительной калибровки и уточнения их параметров в процессе движения объекта [5.5, 5.11].

В таблице 5.1 представлены основные характеристики ряда серийно выпускаемых ДНГ-ДУС [5.7,5.12,5.13].