Математические модели ммг.

Математические модели движения ММГ, представляющих собой электромеханические системы, могут быть получены с использованием уравнений Лагранжа-Максвелла второго рода [101].

Математическая модель ммг rl-типа.

Система уравнений движения идеального ММГ RL-типа (рис. 5.43) для случая учета всех трех компонент векторов угловой скорости, угловых и линейных ускорений основания в первом приближении имеет следующий

вид:

F_2ДВ

F_3ДВ,

(5.88)

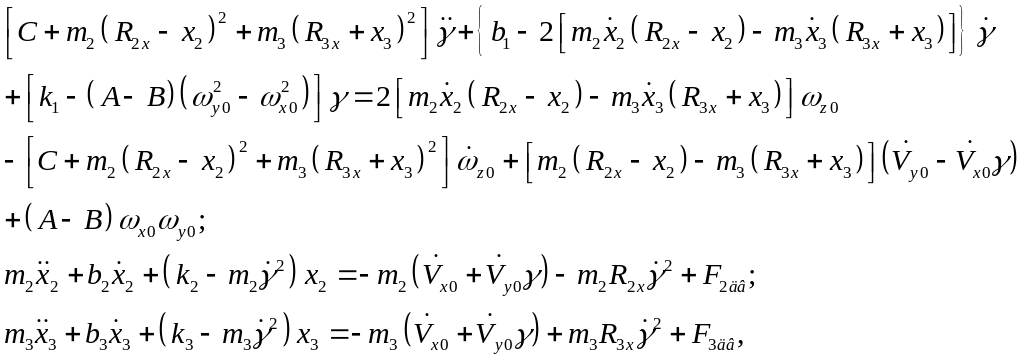
где γ – угол поворота рамки; m₂, m₃ – чувствительные массы; x₂, x₃ – перемещения чувствительных масс; A, B, С – суммарные моменты инерции рамки с инерционными массами соответственно вокруг осей O₁X₁ , O₁Y₁ , O₁Z₁; С₁, С₂, С₃ - соответственно моменты инерции рамки вокруг оси O₁Z₁ и чувствительных масс m₂ и m₃ относительно осей O₂Z₂ и O₃Z₃ ; B₁, B₂, B₃ - моменты инерции рамки вокруг оси O₁Y₁ и чувствительных масс m₂ и m₃ вокруг осей O₂Y₂ и O₃Y₃ соответственно; A₁, A₂, A₃ - моменты инерции рамки вокруг оси O₁X₁ , чувствительных масс m₂ и m₃ вокруг осей O₂X₂ и O₃X₃ соответственно; b₁, b₂, b₃ – коэффициенты демпфирования по соответствующим степеням свободы γ, x₂, x₃; k₁, k₂, k₃ – коэффициенты жесткости по соответствующим степеням свободы; R_2x, R_3x – расстояния от оси O₀Z₀ до центров масс m₂ и m₃ соответственно; ω_x0 , ω_y0 , ω_z0 – проекции угловой скорости основания; V_x0, V_y0 – проекции линейной скорости основания; F_2ДВ , F_3ДВ – развиваемые вибрационными двигателями знакопеременные силы, действующие на массы m₂ и m₃.

Первое уравнение в (5.88) описывает движение рамки по выходной координате γ; второе и третье уравнения – движения чувствительных масс m₂, m₃ вдоль осей O₂X₂ и O₃X₃ соответственно.

Для случая симметричной конструкции подвеса:

где - соответственно амплитуда и частота знакопеременной силы.

Тогда, с учетом выполнения условий

k>>mγ'², F>>m(V'_x0+V'_y0γ)+mRγ'², R>>x_i, i=2,3

уравнения движения чувствительных масс принимают вид:

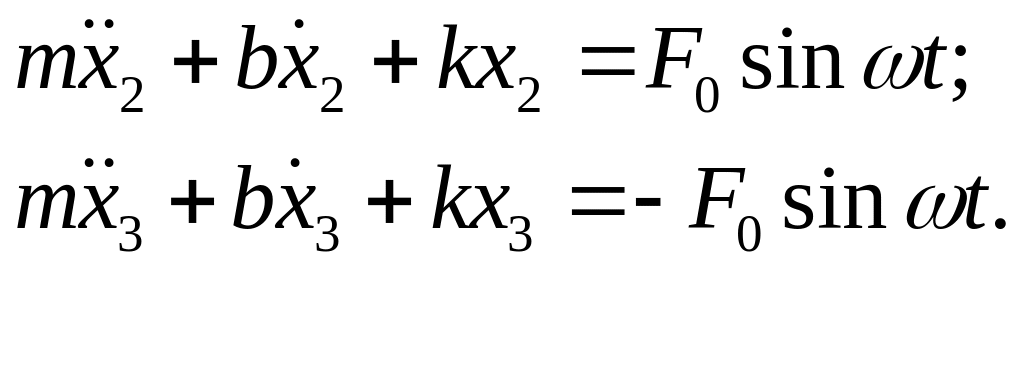(5.89)

Полагаем, что подвес по всем трем степеням свободы настроен на резонанс с силой, развиваемой вибрационным двигателем:

, где .

В этом случае вынужденное решение (5.89) таково:

где ; - добротность подвеса массы.

Подставляя полученное решение для x₂, x₃ в первое уравнение системы (5.88), пренебрегая при этом величиной гироскопического момента в сравнении с моментом демпфирующим во втором слагаемом (с фигурными скобками) в левой части уравнения (5.88), получаем уравнение движения рамки в следующем виде:

(5.90)

где .

Гироскопический момент порождает информационное движение по , амплитуда которого пропорциональна измеряемой угловой скорости . Аддитивные инерционный и центробежный моменты в (5.90) вызывают, в отличие от информационного гироскопического момента, квазипостояные угловые смещения рамки, и сигнал, порождаемый ими, отфильтровывается в синхронном детекторе на выходе прибора. В этой связи (5.90) можно представить так:

, (5.91)

где .

Для случая резонанса решение (5.91) таково:

(5.92)

где - добротность подвеса рамки.