§ 7.4. Задачи линейного программирования

Рассмотрим простейший случай: выбор показателя эффективности W явно диктуется целевой направленностью операции, а ее условия известны заранее (детерминированная задача). В этом случае показатель эффективности зависит только от двух групп параметров: заданных условий  и элементов решения х. Т. е. W = W{,x).

Пусть решение х представляет собой n-мерный вектор:

х = (х₁, х₂, ..., x_n), где х_i – элементы решения

Требуется найти такие значения х₁, х₂, ..., x_n, которые обращают величину W в экстремум.

Трудности, возникающие при решении задач математического программирования, зависят:

а) от вида функциональной зависимости, связывающей W с элементами решения,

б) от «размерности» задачи, т. е. от количества элементов решения х₁, х₂, ..., x_n и

в) от вида и количества ограничений, наложенных на элементы решения.

Среди задач математического программирования самыми простыми (и лучше всего изученными) являются так называемые задачи линейного программирования. Характерно для них то, что:

а) показатель эффективности (целевая функция) W линейно зависит от элементов решения х₁, х₂, ..., x_n и

б) ограничения, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно х₁, х₂, ..., x_n. Линейные зависимости часто встречаются на практике.

Приведем несколько примеров задач линейного программирования.

1. Задача о пищевом рационе.

Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П₁, П₂, П₃, П₄. Стоимость единицы каждого продукта равна соответственно c₁, c₂, c₃, c₄. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее b₁ единиц; углеводов— не менее b₂ единиц; жиров — не менее b₃ единиц. Для продуктов П₁, П₂, П₃, П₄ содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано таблицей

Элементы Продукты	Белки	Углеводы	Жиры
П1	a11	a12	a13
П2	a21	a22	a23
П3	a31	a32	a33
П4	a41	a42	a43

где a_ij (i = 1, 2, 3, 4; j = 1, 2, 3) — некоторые определенные числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры). Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П₁, П₂, П₃, П₄, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

Составим математическую модель. Обозначим через x₁, x₂, x₃, x₄ количества продуктов П₁, П₂, П₃, П₄, входящих в рацион. Показатель эффективности, который требуется минимизировать, — стоимость рациона (обозначим её L); она линейно зависит от элементов решения x₁, x₂, x₃, x₄: L = c₁ x₁ + c₂ x₂ + c₃ x₃ + c₄ x_4..

Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам и жирам:

Эти линейные неравенства представляют собой ограничения, налагаемые на элементы решения x₁, x₂, x₃, x₄. Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных x₁, x₂, x₃, x_4, чтобы они удовлетворяли ограничениям — неравенствам и одновременно обращали в минимум линейную функцию этих переменных: L = c₁ x₁ + c₂ x₂ + c₃ x₃ + c₄ x₄  min

2. Задача о планировании производства.

Предприятие производит изделия трех видов: И₁, И₂, И₃. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить не менее b₁ единиц изделия И₁, не менее b₂ единиц изделия И₂ и не менее b₃ единиц изделия И₃. План может быть перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: не более соответственно ₁, ₂, ₃ единиц. На изготовление изделий идет какое-то сырье; всего имеется четыре вида сырья: S₁, S₂, S₃, S₄, причем запасы ограничены числами ₁, ₂, ₃, ₄ единиц каждого вида сырья. Теперь надо указать, какое количество сырья каждого вида идет на изготовление каждого вида изделий. Обозначим a_{i j} количество единиц сырья вида S_j (j = 1,2,3,4), потребное на изготовление одной единицы изделия И_i, (i = 1, 2, 3). Первый индекс у числа a_{i j} — вид изделия, второй — вид сырья. Значения a_{i j} сведены в матрицу.

Сырьё Изделия	S1	S2	S3	S4
И1	a11	a12	a13	a14
И2	a21	a22	a23	a24
И3	a31	a32	a33	a34

При реализации одно изделие И_i приносит предприятию прибыль c_i. Требуется так спланировать производство (сколько каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась в максимум.

Запишем задачу в форме ЗЛП.

Элементами решения будут x₁, x₂, x₃ – количества единиц изделий U₁, U₂, U₃, которые мы произведём.

Запишем условия – ограничения.

Обязательность выполнения плана:

Отсутствие затоваривания:

Нам должно хватить сырья:

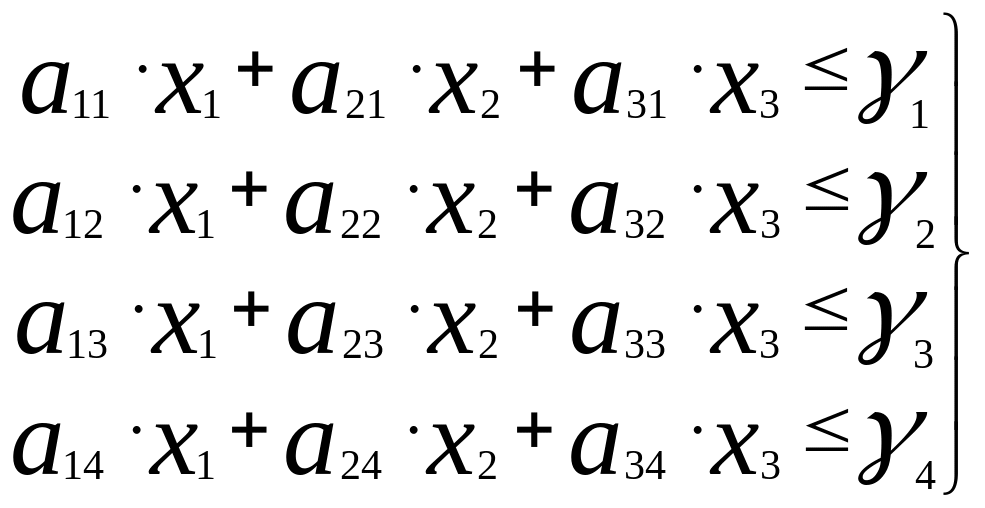
Теперь целевая функция: прибыль, приносимая планом

L = c₁ x₁ + c₂ x₂ + c₃ x₃  max

Таким образом, мы снова получили ЗЛП.

3. Задача о загрузке оборудования.

Ткацкая фабрика располагает двумя видами станков, из них N₁ станков типа 1 и N₂ станков типа 2. Станки могут производить три вида тканей: Т₁, Т₂, Тз, но с разной производительностью. Данные a_ij производительности станков даны в таблице (первый индекс — тип станка, второй — вид ткани).

Ткань Станок	T1	T2	T3
1	a11	a12	a13
2	a21	a22	a23

Каждый метр ткани вида T₁ приносит фабрике доход c₁, вида Т₂ — доход c₂, Т₃ — доход с₃. Фабрике предписан план, согласно которому она должна производить в месяц не менее b₁ метров ткани Т₁, b₂ метров ткани Т₂, b₃ метров ткани Т_3. Количество метров каждого вида ткани не должно превышать соответственно ₁, ₂, ₃ метров. Кроме того, все без исключения станки должны быть загружены. Требуется так распределить загрузку станков производством тканей Т₁, Т₂, Т₃, чтобы суммарный месячный доход был максимален.

На первый (легкомысленный) взгляд эта задача - родная сестра предыдущей. Но если мы примем за x₁, x₂, x₃ количества тканей трёх видов, то не сможем учесть возможности оборудования. Что же здесь является элементами решения? Возможно, количество станков 1 и 2 вида, занятыми производством тканей каждого вида. Для удобства обозначим элементы решения буквами x с двумя индексами: первый – тип станка, второй - вид ткани. Всего будет шесть элементов решения

x₁₁ x₁₂ x₁₃

x₂₁ x₂₂ x₂₃

Здесь x_ij -количество станков i–ого вида, занятых изготовлением ткани j–ого вида.

Запишем условия-ограничения.

Все станки должны быть задействованы:

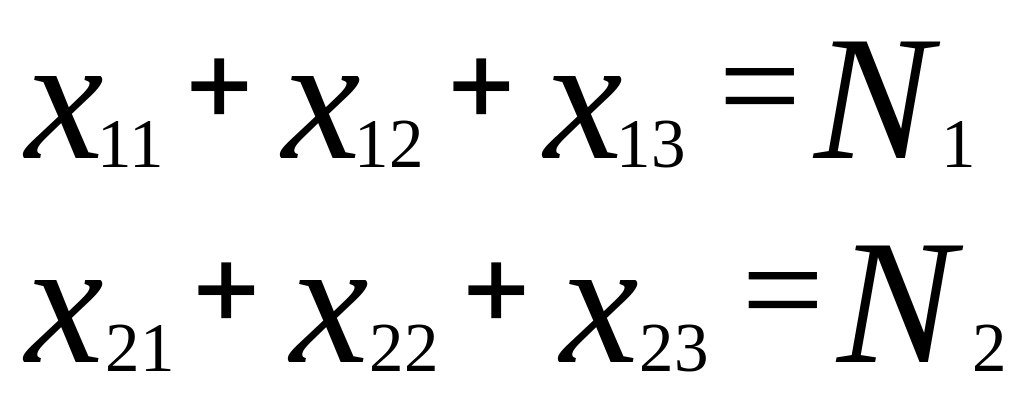
Обеспечим выполнение плана:

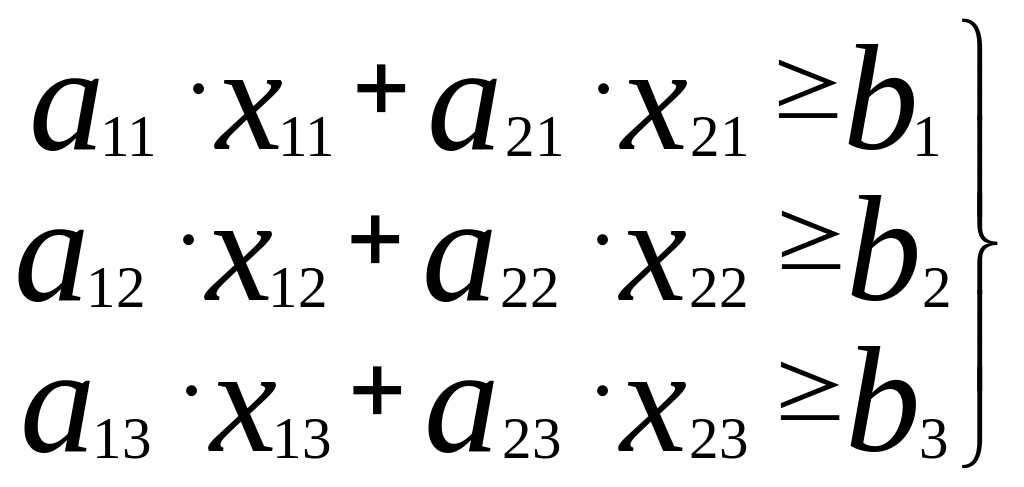
Ограничим перевыполнение плана:

Запишем суммарный доход от производства всех видов тканей. Суммарное количество метров ткани Т₁, произведённое всеми станками, равно a₁₁  x₁₁ + a₂₁  x₂₁, и принесёт доход c₁(a₁₁ x₁₁ + a₂₁ x₂₁). Суммарный доход равен

L = c₁(a₁₁ x₁₁ + a₂₁ x₂₁) + c₂ (a₁₂ x₁₂ + a₂₂ x₂₂) + c₃ (a₁₃ x₁₃ + a₂₃ x₂₃)  max

4. Задача о снабжении сырьем.

Имеются три промышленных предприятия: П₁, П₂, П₃, требующих снабжения определенным видом сырья. Потребности в сырье каждого предприятия равны соответственно a₁, a₂, a₃ единиц. Имеются пять сырьевых баз, расположенных от предприятий на каких-то расстояниях и связанных с ними путями сообщения с разными тарифами. Единица сырья, получаемая предприятием П_i, с базы Б_j обходится предприятию в c_{i j} рублей (первый индекс — номер предприятия, второй — номер базы)

Базы Предприятия	Б1	Б2	Б3	Б4	Б5
П1	с11	с12	с13	с14	с15
П2	с21	с22	с23	с24	с25
П3	с31	с32	с33	с34	с35

Возможности снабжения сырьем с каждой базы ограничены ее производственной мощностью: b₁, b₂, b₃, b₄, b₅ единиц сырья. Требуется составить такой план снабжения предприятий сырьем (с какой базы, куда и какое количество сырья везти), чтобы потребности предприятий были обеспечены при минимальных расходах на сырье.

Поставим задачу линейного программирования. Обозначим x_ij количество сырья, получаемого i-ым предприятием c j-ой базы. Всего план будет состоять из 15 элементов решения:

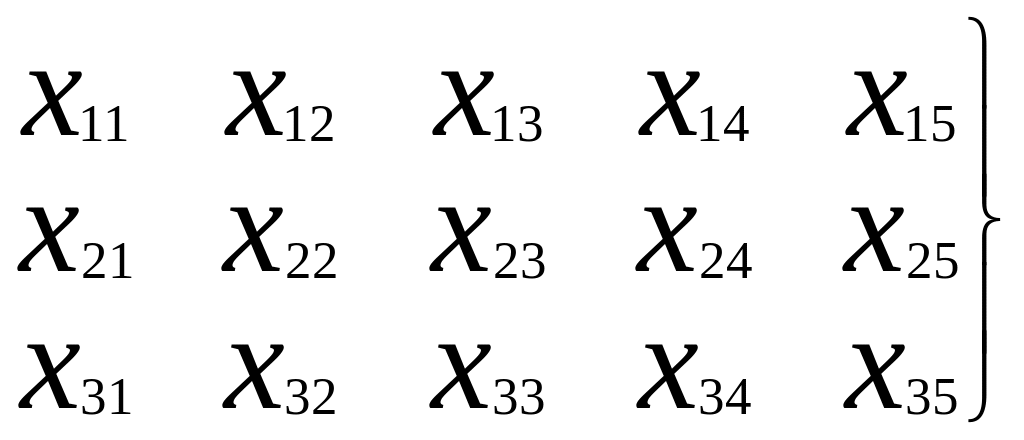
Введём ограничения по потребностям. Они состоят в том, что каждое предприятие получит нужное ему количество сырья (ровно столько, сколько ему нужно):

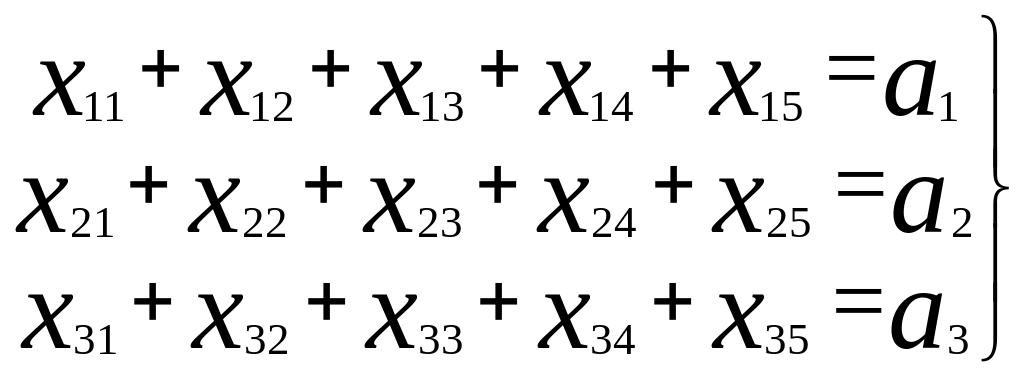
Теперь запишем ограничения-неравенства, вытекающие из производственных мощностей баз: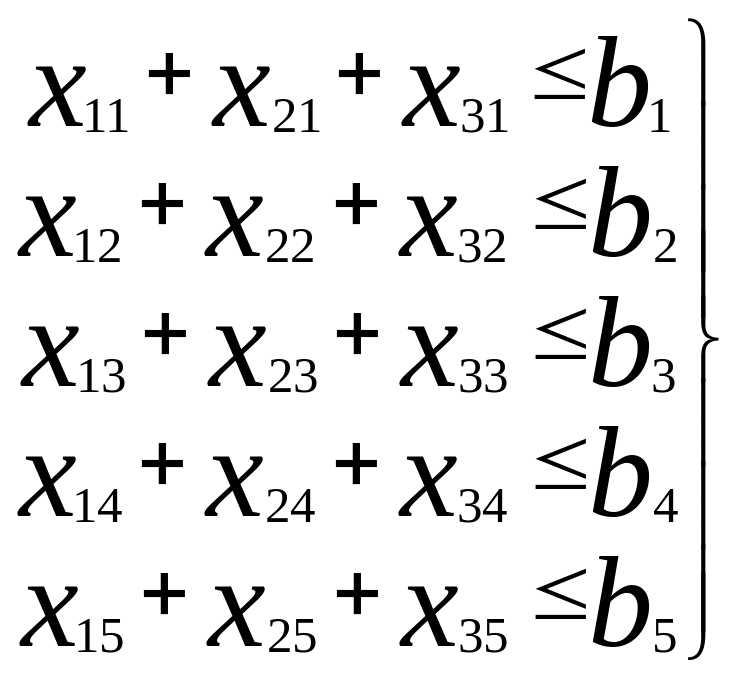

Запишем суммарные расходы на сырьё, которые мы хотим минимизировать. С учётом данных таблицы тарифов получим .