§ 7.5. Основная задача линейного программирования

Существует стандартная форма задачи линейного программирования, так называемая «основная задача линейного программирования» (ОЗЛП), которая формулируется так: найти неотрицательные значения переменных х₁, х₂, ..., x_n , которые удовлетворяли бы условиям-равенствам

(3)

и обращали бы в максимум линейную функцию этих переменных:

L = c₁ x₁ + c₂ x₂ +…+ c_n x_n  max. (4)

Любую задачу линейного программирования можно свести к ОЗЛП.

Возможен и обратный переход: от ОЗЛП к задаче с ограничениями-неравенствами.

Назовём допустимым решением ОЗЛП всякую совокупность неотрицательных значений х₁, х₂, ..., x_n,, удовлетворяющую условиям (3). Оптимальным назовём то из допустимых решений, которое обращает в максимум функция (4).

Это решение существует не всегда.

Во-первых, может оказаться, что уравнения (3) несовместны (противоречат друг другу).

Во-вторых, может оказаться, что они совместны, но не в области неотрицательных значений.

В-третьих, может быть и так, наконец, что допустимые решения ОЗЛП существуют, но среди них нет оптимальных, т.к. функция L в ОДР не ограничена сверху.

§ 7.6. Геометрическая интерпретация озлп

Пусть имеется m условий – равенств (3). Предположим для простоты, что все они линейно независимы. Пусть также число линейно независимых уравнений m на 2 меньше числа переменных n (n-m=k=2). Именно такой частный случай даёт возможность геометрической интерпретации на плоскости.

Мы знаем, что m линейно независимых уравнений всегда можно разрешить для m базисных переменных, выразив их через остальные свободные, число которых равно в примере n-m=k=2.

П редположим, что свободные переменные x₁ и x₂, а остальные x₃, x₄,…x_n – базисные. Тогда вместо m уравнений (3) получают m уравнений, разрешаемых относительно x₃, x₄,…x_n.

(5)

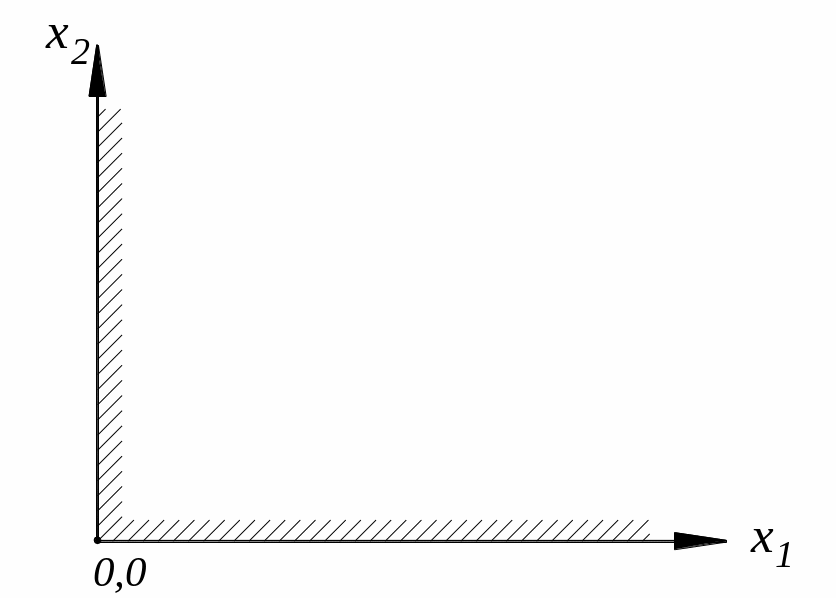
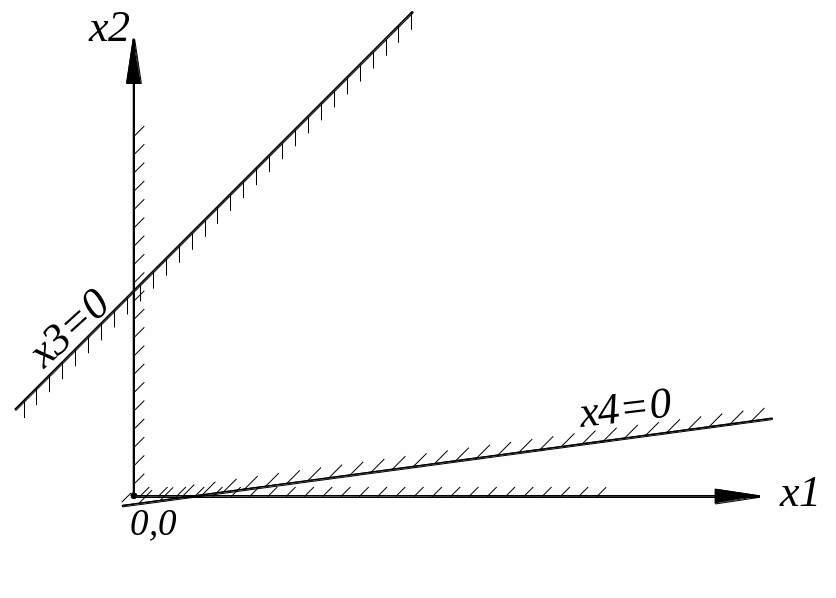
Рассмотрим плоскость х₁Ох₂. Поскольку х₁ и х₂ должны быть больше или равны 0, то допустимые значения свободных переменных выше оси Ох₁ и правее оси Ох₂. Покажем это штриховкой.

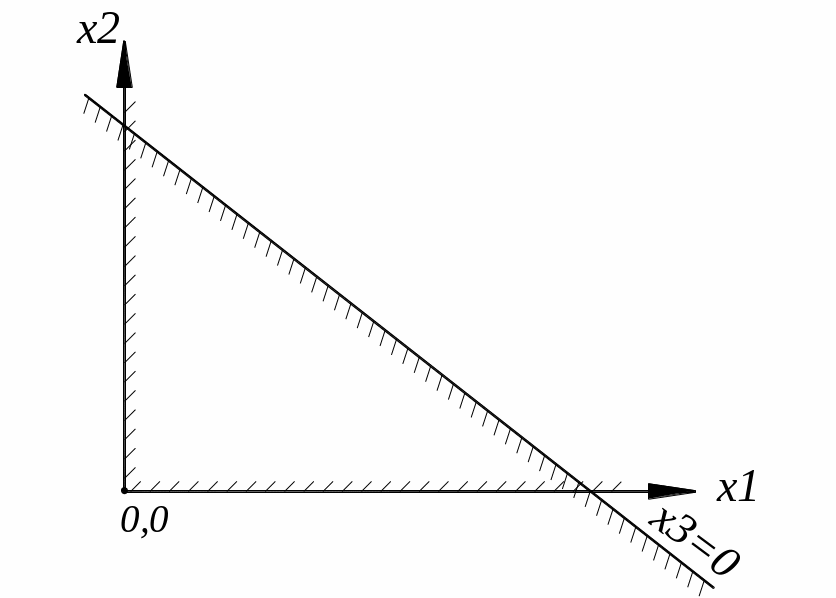
Построим на плоскости х₁Ох₂ область допустимых решений (ОДР) или убедимся, что её не существует. Базисные переменные x₃, x₄,…x_n должны быть неотрицательны и удовлетворять условиям (5). Положим в первом уравнении (5) x₃=0 и получим уравнение прямой линии . На этой прямой линии x₃=0. По одну сторону от неё x₃>0, по другую x₃<0. Пусть положительная сторона оказалась ниже и левее прямой x₃=0. Покажем это штриховкой.

Аналогично поступим и со всеми остальными условиями (5).

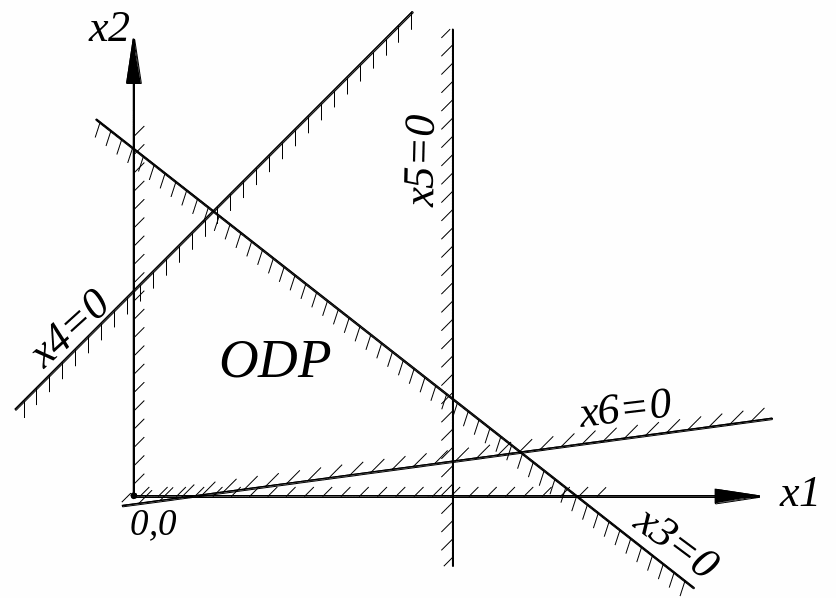
Каждое из них изображается прямой со штриховкой, указывающей «допустимую» полуплоскость, где только и может лежать решение.

Мы построим n прямых: две оси и n–2 прямых x₃=0, x₄=0, … , x_n=0. Каждая из них определяет «допустимую» полуплоскость. Часть первого квадранта, принадлежащая одновременно всем этим полуплоскостям, и есть область допустимых решений.

Может оказаться, что ОДР не существует, а значит, уравнения (5) несовместны в области неотрицательных значений переменных или вообще несовместны. Также может оказаться, что ОДР существует, но не замкнута.

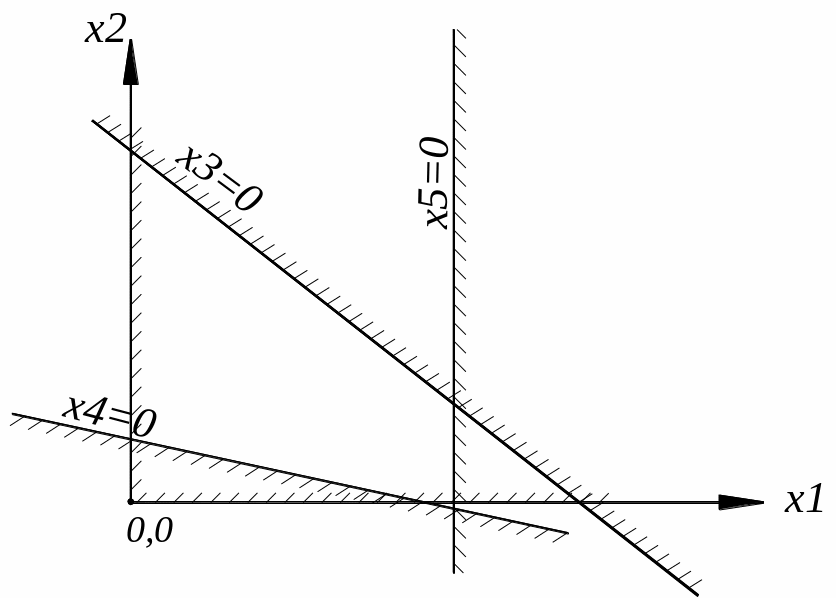
Предположим, что ОДР существует, замкнута и мы её построили. Она представляет собой неправильный многоугольник. Как найти оптимальное решение среди решений из этой области?

Для этого дадим геометрическую интерпретацию (4) L  max. Подставив выражения (5) в (4) выразим L через свободные переменные х₁ и х₂. После приведения подобных членов получим

(6)

Отбросим свободный член ₀, т.к. максимум функции L достигается при тех же значениях, что и максимум функции

(7)

Изобразим геометрически условие L^’  max. Положим сначала L^’=0, т.е. ₁x₁+₂x₂=0 и построим на плоскости прямую с таким уравнением; она проходит через начало координат.

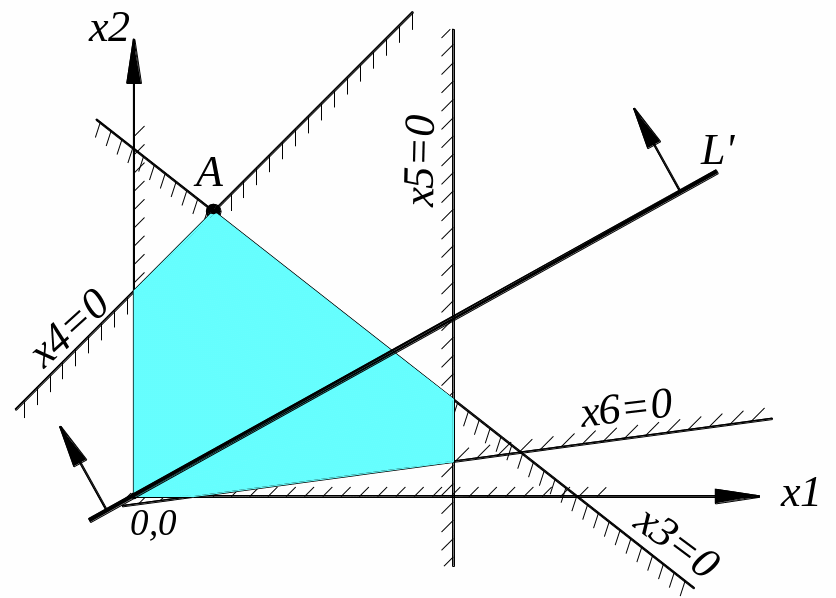
Назовём её опорной прямой. Если будем придавать некоторые значения С₁, С₂, С₃,…, прямая будет перемещаться параллельно самой себе. При перемещении в одну сторону L^’ будет возрастать, в другую – убывать. Отметим на чертеже стрелками направление, в котором L^’ возрастает. L^’ достигает максимума в точке А, крайней точке ОДР в направлении стрелок. В этой точке свободные переменные принимают оптимальное значение x₁^* и x₂^*. Из них по (5) можно найти оптимальные значения других, базисных переменных x₃^*, x₄^*,… x_n^*. Максимум достигается в одной из вершин ОДР, где по крайней мере две базисные переменные (х₃ и х₄) равны нулю.

Если ОДР не ограничена сверху, то оптимального решения на существует. В разумно поставленных задачах такого недоразумения не возникает.

Также может быть, что оптимальное решение есть, но оно не единственное, их бесконечное множество. Максимум достигается на отрезке АВ, параллельном опорной прямой, т.е. и в вершине А, и в вершине В. т.е. и в этом случае можно ограничиться поиском в вершинах.

Итак, оптимальное решение, если оно существует, всегда достигается в одной из вершин ОДР, в точке, где по крайней мере k (k=n-m) из переменных x₃, x₄,…x_n равны нулю, а остальные неотрицательны. Это правило справедливо для любого k.