§ 8. Примеры других комбинаторных объектов и сводка некоторых результатов

1. Ч исла Каталана. Рассмотрим следующую задачу, решённую ещё Леонардом Эйлером:

каково число разбиений выпуклого (n+2)-угольника (n  1) на треугольники непересекающимися диагоналями ? Диагональю считается любой отрезок, соединяющий две вершины многоугольника, а разбиение – это произвольное множество треугольников, не имеющих общих внутренних точек, покрывающее весь многоугольник. Например, выбрав произвольную вершину многоугольника, можно из неё провести все диагонали в другие вершины и получить одно из возможных разбиений. Обозначим искомое число разбиений через K_n – это и есть числа Каталана.

Легко понять, что K₁ = 1, K₂ = 2, K₃ = 5. В общем случае перенумеруем вершины (n+2)-угольника числами 1, … , i, … , n+2 и рассмотрим любой треугольник с вершинами 1, i, n+2 (2  i  n+1). Любое разбиение исходного (n+2)-угольника, содержащее этот треугольник, получается комбинированием любого разбиения на треугольники i-угольника M, рассматриваемого треугольника и произвольного разбиения на треугольники (n+3–i)-уголь­ника N (смотри рисунок выше). В случае, когда i = 3 или i = n, многоугольники M или N превращаются в треугольники, а в случае i = 2 или i = n+1 – они вырождаются. Для применимости предыдущих рассмотрений удобно считать, что K₀ = 1. Каждое разбиение исходного (n+2)-угольника на треугольники обязательно содержит некоторый треугольник с вершинами 1, i, n+2, поэтому получаем следующую рекуррентную формулу:

.

Для нахождения общей формулы можно воспользоваться методом производящих функций. Если , то

. Значит, K(x) удовлетворяет уравнению x·K(x)² – K(x) + 1 = 0, решением которого является функция . Воспользовавшись разложением в ряд

,

получим

Следовательно, . Ясно, что знак + не подходит ввиду неотрицательности степеней переменной в K(x). Значит, сравнивая коэффициенты, получим формулу для чисел Каталана

(i  N₀).

Числа Каталана возникают в разнообразных комбинаторных задачах. Например, можно показать, что количество следующих объектов равно K_n :

• число всех последовательностей (₁ ; … ; _2·n) длины 2n, в которых _i  {–1, 1} (1  i  2·n), ;

• число всех последовательностей, состоящих из n открывающих и n закрывающих скобок, в которых для любой позиции количество закрывающих скобок слева не превосходит количества открывающих скобок слева;

• число всех (2n)-матриц с компонентами 1, 2, … , 2·n, расположенными в порядке возрастания в каждой строке и каждом столбце;

• число всех монотонных функций f : {1, … , n}  {1, … , n} со свойством f(i)  i при любом i  {1, … , n};

• число бинарных деревьев (см. Конспект лекций по дискретной математике, § 6 главы III).

Конечно, можно легко найти обобщение чисел Каталана: например числа , где q – заданное натуральное число (i  N₀).

Числа Стирлинга первого рода. Рассмотрим произвольную подстановку на n символах 1, … , n : . Как известно, она может быть разложена (однозначно с точностью до порядка) в произведение независимых циклов, включая тривиальные: .

Алгоритм такого разложения прост и может быть проиллюстрирован на примере подстановки  = : находим нетривиальный цикл 1  2  5  6  1 и рассматриваем подстановку

(1, 2, 5, 6) ^–1· = (6, 5, 2, 1)· = = ₁ ,

которая имеет меньше перемещаемых символов, чем . Повторяя с ней ту же процедуру, находим нетривиальный цикл 3  4  7  3 и рассматриваем подстановку

(3, 4, 7) ^–1·₁ = (7, 4, 3)· = =  –

тождественная подстановка. Таким образом, (3, 4, 7) ^–1·(1, 2, 5, 6) ^–1· = , и значит,  = (1, 2, 5, 6)·(3, 4, 7) – произведение двух нетривиальных циклов. Та же подстановка может быть записана в виде произведения трёх циклов:  = (1, 2, 5, 6)·(3, 4, 7)·(8), включая тривиальный цикл (8).

Тождественная подстановка  на n символах раскладывается в произведение n тривиальных циклов:  = (1)·(2)· … ·(n). Это единственная подстановка на n символах, раскладывающаяся в произведение n циклов.

Каноническим разложением подстановки называется такое её разложение в произведение независимых циклов, что в каждом цикле наименьший элемент стоит на первом месте и эти наименьшие элементы не убывают в порядке следования циклов. Например, разложение (1, 2, 5, 6)·(3, 4, 7)·(8) – каноническое, а следующие разложения той же подстановки (2, 5, 6, 1)·(3, 4, 7)·(8), (1, 2, 5, 6)·(4, 7, 3)·(8), (8)·(1, 2, 5, 6)·(3, 4, 7) – не канонические. Если в каноническом разложении стереть скобки, то получится перестановка чисел 1, … , n. Например, для рассмотренной подстановки  получится перестановка  = (1, 2, 5, 6, 3, 4, 7, 8). Оказывается, что сопоставление    является биективным.

Число Стирлинга первого рода обозначается через равно числу подстановок на n символах, разлагающихся в k циклов, включая тривиальные. При этом по определению полагают = 1, = 0 (k > 0), = 0 (n > 0), = 1, = 0 (k > 1).

Приведём таблицу начальных значений величин :

n
0	1	0	0	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0	0	0	0
2	0	1	1	0	0	0	0	0	0	0
3	0	2	3	1	0	0	0	0	0	0
4	0	6	11	6	1	0	0	0	0	0
5	0	24	50	35	10	1	0	0	0	0
6	0	120	274	225	85	15	1	0	0	0
7	0	720	1764	1624	735	175	21	1	0	0
8	0	5040	13068	13132	6769	1960	322	28	1	0
9	0	40320	109584	118124	67284	22449	4536	546	36	1

Какой рекуррентной формулой связаны числа Стирлинга первого рода ? Если подстановка  на (n+1)-м символе разложена в произведение m независимых циклов  = с₁·…·c_m , то ровно один из этих циклов содержит n+1, а произведение остальных циклов даёт подстановку на n символах, раскладывающуюся в произведение (m – 1)-го цикла.

Если цикл с n+1 тривиален, то подстановка  получена из подстановки на n символах c (m–1)-м циклом дописывание в конце тривиального цикла (n+1). Таких подстановок . Если же цикл с n+1 не тривиален, то он получен из некоторого цикла для подстановок на n символов с помощью вставки числа n+1 не на первое место. Таким образом, в этом случае  получается из подстановки на n символах с m циклами путём вставки в некоторый из циклов элемента n+1 не на первое место. Учитывая отмеченное выше биективное соответствие разложений с перестановками, получим возможностей конструирования подстановок  в этом случае. Итак, получена рекуррентная формула

, = 1, = 0 (k > 0), = 0 (n > 0),

которая вместе с приведёнными начальными условиями позволяет вычислять числа Стирлинга первого рода. Некоторые важные свойства этих чисел будут приведены ниже в разделе 4 этого параграфа.

2. Числа Стирлинга второго рода. Число Стирлинга 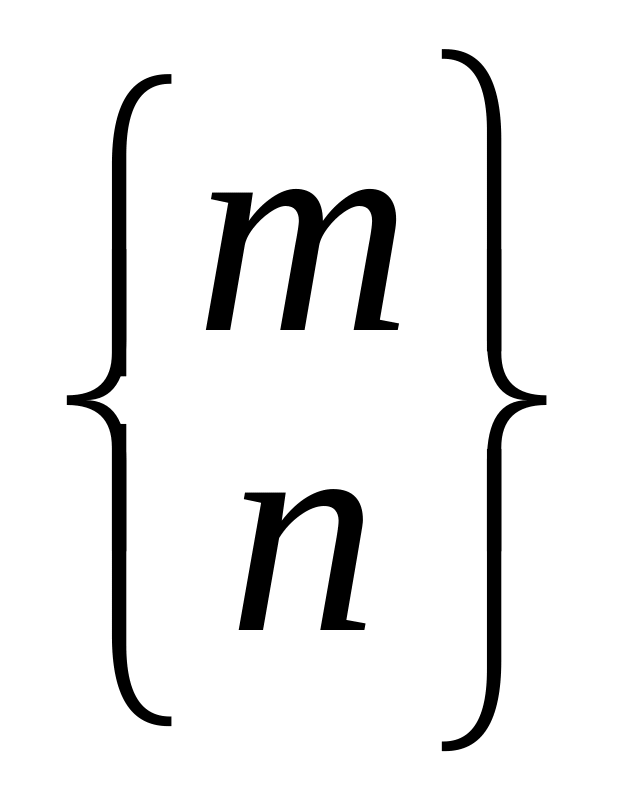второго рода – это количество разбиений n-элементного множества в объединение m непересекающихся подмножеств (порядок подмножеств не учитывается). При этом по определению полагают = 1, = 0, = 0. Приведём таблицу начальных значений этих величин:

n
0	1	0	0	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0	0	0	0
2	0	1	1	0	0	0	0	0	0	0
3	0	1	3	1	0	0	0	0	0	0
4	0	1	7	6	1	0	0	0	0	0
5	0	1	15	25	10	1	0	0	0	0
6	0	1	31	90	86	15	1	0	0	0
7	0	1	63	301	350	140	21	1	0	0
8	0	1	127	966	1701	1050	266	28	1	0
9	0	1	255	3025	7770	6951	2646	462	36	1

Вывести рекуррентную формулу для чисел Стирлинга второго рода несложно. Если есть какое-либо разбиение m-элементное разбиение (n+1)-эле­ме­нтного множества, то ровно одному из множеств разбиения принадлежит n + 1. Если это множество одноэлементно, то рассматриваемое разбиение получено добавлением к (m–1)-элементному разбиению n-эле­ментного множества ещё одного множества {n+1}. Так можно получить разбиение. Если же множество разбиения, содержащее n + 1, содержит более одного элемента, то рассматриваемое разбиение получено добавлением n + 1, к одному из m-элементных разбиений n-элементного множества. Таких возможностей конструирования будет m· .

В итоге получаем рекуррентную формулу

.

Она вместе с приведёнными начальными условиями позволяет вычислять числа Стирлинга первого рода. Некоторые важные свойства этих чисел будут приведены ниже в разделе 4 этого параграфа.

3. Некоторые важные формулы-свойства рассмотренных чисел. Приведём некоторые полезные свойства биномиальных коэффициентов и чисел Стирлинга первого и второго родов. Всюду обозначение r относится к действительным числам, а n и m – к натуральным или целым. Использование действительных чисел оправдано тем, что выражения являются многочленами от r. Через _{m, n} обозначается символ Кронекера : эта величина равна 1, если m = n, и равна 0 в противном случае.

Конечно, приведённые формулы не претендуют на полноту, их пополнение – непрерывная забота каждого математика.