§ 6. Принцип включения-исключения

Следующий важный комбинаторный результат с успехом можно использовать в различных ситуациях:

Теорема (принцип включения-исключения). Пусть имеется n объектов и m свойств, которыми могут обладать эти объекты. Обозначим через n(i₁ , … , i_k ) количество объектов, обладающих i₁-м, i₂-м, … , i_k-м свойствами одновременно, а через n₀ – количество объектов, не обладающих ни одним из рассматриваемых свойств. Тогда справедлива формула:

Доказательство. Индукция по m. Если рассматривается только одно свойство, очевидно, n₀ = n – n(1) – это и есть доказываемая формула. Предположим, что формула верна для m–1 свойства и докажем её для m свойств.

Обозначим через n( ) число объектов, не обладающих ни одним из свойств i₁ , … , i_s , а через n( , j₁ , … , j_t ) – число объектов, не обладающих ни одним из свойств i₁ , … , i_s , но обладающих свойствами j₁ , … , j_t . Ограничиваясь свойствами с номерами 1, … , m–1, рассматриваемых на те же n объектах, и применяя предположение индукции, получим

Эту формулу для свойств с номерами 1, … , m–1 можно применять и к множеству объектов, обладающих свойством m:

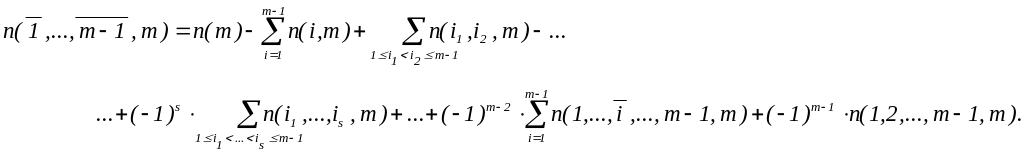
Ясно, что n₀ = n( ) = n( ) – n( , m). Поэтому, вычитая полученные по предположению индукции формулы, получим:

что и требовалось.

Теорема доказана.

Эта теорема, конечно, обобщает принцип дополнения: если взять m = 1, то формула будет очевидной n₀ = n – n(1).

Следствие 1 (о числе элементов дополнения). Для произвольных подмножеств A₁ , …, A_m множества A справедлива формула

Следствие 2 (о числе элементов множества). Если A = A₁  …  A_m , то

Примеры: 1. В классе 25 учеников. Из них 15 человек изучают английский язык и 15 немецкий. Сколько учеников изучают сразу оба языка?

Если А – множество учеников, изучающих английский язык, Н – множество учеников, изучающих немецкий язык, а К – множество всех учеников в классе, то К = А  Н и

25 = |А  Н| = |A| + |H| – |A  H| = 30 – |A  H|,

откуда |A  H| – количество учеников, изучающих сразу оба языка равно 5.

2. В лыжной секции на 5 спортсменов больше, чем в секции волейбола, а футболистов в два раза больше, чем волейболистов. При этом шестая часть футболистов занимается волейболом, среди волейболистов не менее 7 лыжников, но лыжники не занимаются футболом. Сколько спортсменов занимаются в этих трёх секциях, если их количество на 25 больше, чем количество лыжников ?

Имеем x = |Л| + |В| + |Ф| – |Л  В| – |В  Ф| = = (x – 25)+(x – 30)+2·(x–30)–|Л  В| – = = – 105 – |Л  В|, |Л  В| = – 105  7, т.е. 8·x  336, x  42.

Из ,  Z следует, что x  3. Если взять x = 42, то |Л| = 17, |В| = 12, |Ф| = 24, |В  Ф| = 4, |Л  В| = 7. Значит, спортсменов в трёх секциях не менее 42. Поскольку |Л  В| – |В  Ф|  |В|, получим условие – 105 +  x – 30, 3·x – 115  x – 30, 2·x  85, x  42 (x целое!). Значит, в секциях занимаются ровно 42 спортсмена.