§ 4. Метод производящих функций для решения общего линейного однородного рекуррентного соотношения с постоянными коэффициентами

Рассуждения, аналогичные использованным, можно применить для нахождения общего решения произвольного линейного однородного рекуррентного соотношения с постоянными коэффициентами

f(n + k) = a₁f(n + k – 1) + … + a_kf(n).

Теорема. Следующие условия для последовательности {u_n} комплексных чисел эквивалентны:

(1) последовательность {u_n} является решением линейного однородного рекуррентного соотношения с постоянными коэффициентами

f(n + k) = a₁f(n + k – 1) +… + a_kf(n).

(2) u_n = , где ₁ , … , _s – различные корни характеристического уравнения () = 0 кратностей r₁ , … , r_s соответственно, где () = ^k – a₁^k–1 –…– a_k–1 – a_k – характеристический многочлен, (это значит, что ^k – a₁^k–1 – … – a_k–1 – a_k = ( – ₁) …( – _s) ), а P_i(x) – некоторый многочлен, степень которого меньше соответствующей кратности r_i (1  i  s).

Доказательство. (1)  (2) Если u_n+k = a₁u_n+k–1 +…+ a_ku_n (n  N₀), то умножая каждое из этих равенств на xⁿ и складывая, получим:

u_kx⁰ + u_k+1x¹+… = a₁( u_k–1x⁰ + u_kx¹+…)+…+a_k(u₀x⁰+u₁x¹+ …) 

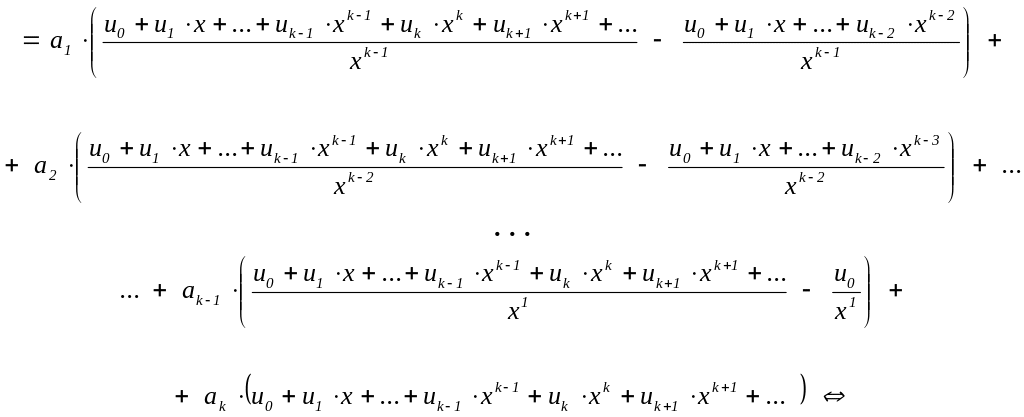
 u(x)(1–a₁x–a₂x²– … –a_k–1x^k–1–a_kx^k) =

= (u₀+u₁x+…+u_k–1x^k–1) – a₁x(u₀+u₁x+…+u_k–2x^k–2)– … – a_k–1x^k–1u₀ .

В правой части этого равенства стоит многочлен

P(x) = (u₀+u₁x+…+u_k–1x^k–1) – a₁x(u₀+u₁x+…+u_k–2x^k–2)– … – a_k–1x^k–1u₀

степени не выше k–1, так что u(x) = , что и требовалось.

(2)  (3) Пусть u(x) = , где P(x) – многочлен степени не выше k–1. Разложим многочлен x^k – a₁x^k–1 – … – a_k–1x – a_k в произведение линейных множителей над алгебраически замкнутым полем C:

x^k – a₁x^k–1 – … – a_k–1x – a_k = (x – ₁) …(x – _s) ,

где ₁ , … , _s – попарно различные корни кратностей r₁ , … , r_s .

Ясно, что 1 – a₁x – … – a_kx^k =

=

= (1 – ₁x)  … (1 – _sx) .

Поэтому производящую функцию u(x) можно представить в виде

u(x) =

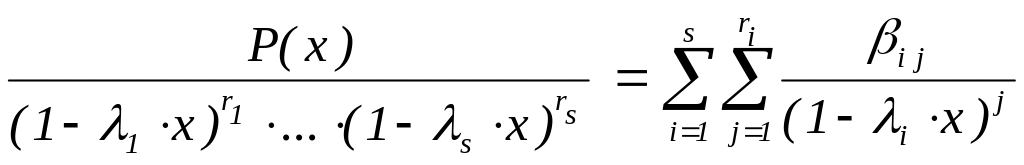
разложения в сумму простых дробей, где _ij  C (1  i  s, 1  j  r_i). Здесь важно учитывать, что степень числителя P(x) меньше степени знаменателя. Воспользовавшись разложениями в ряд

, получим

u(x) =

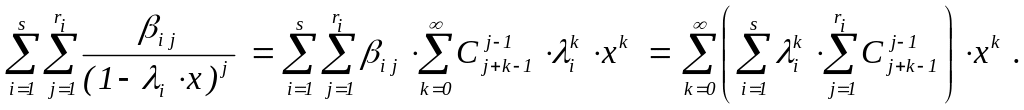
По определению производящей функции, коэффициент при степенях переменной x равен соответствующему члену последовательности.

Значит, (k  N₀). При этом участвующую здесь сумму можно рассматривать как многочлен от k, степень каждого из выделенных слагаемых в котором не превосходит j–1 , в целом степень многочлена не превосходит r_i – 1. Обозначая этот многочлен через P_i(x), получим: , что и требовалось.

(3)  (1) Пусть теперь , где степень многочлена P_i(x) не превосходит r_i – 1, т.е. .

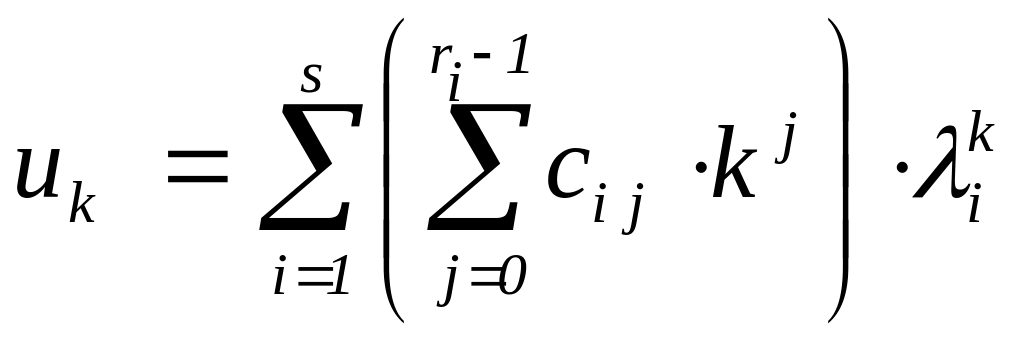Нужно доказать, что такая последовательность будет решением рассматриваемого линейного однородного рекуррентного соотношения с постоянными коэффициентами.

Ввиду линейной структуры решений этого соотношения достаточно проверить, что решениями будут все произведения вида k^j_i^k , где 0  j < r_i . Это значит, что выполнены следующие соотношения:

(n+k)^j^n+k = a₁(n+k–1)^j^n+k–1+…+a_kn^jⁿ ,  = _i , n  N₀ .

Если  = 0 – корень многочлена (x) = x^k – a₁x^k–1 –…– a_k–1x – a_k , то a_k = 0, и соотношения выполняются.

Они будут выполнены и в случае j = 0, т.к. ^k = a₁^k–1 + …+ a_k–1 + a_k .

В случае j  1 воспользуемся формулой бинома Ньютона

:

(n+k)^j^n+k = a₁(n+k–1)^j^n+k–1+…+a_kn^jⁿ 

 (n+k)^j^k = a₁(n+k–1)^j^k–1+…+a_k–1(n+1)^j+a_kn^j 

 .

Докажем, что совпадают коэффициенты при всех степенях n, т.е.

^k = a₁^k–1 + … + a_k–1 + a_k (для n^j),



 ^k–1kⁱ = a₁^k–2(k–1)ⁱ+…+a_k–22ⁱ+a_k–1 (для n^j–i , i > 0).

Это следует из приводимой ниже леммы.

Теорема доказана.

Лемма (соотношения для r-кратного корня многочлена). Если  – корень кратности r > 0 многочлена f(x) = x^k – a₁x^k–1 – … – a_k–1x – a_k , то справедливы соотношения

^k = a₁^k–1 + … + a_k–1 + a_k ,

^k–1kⁱ = a₁^k–2(k–1)ⁱ+…+a_k–22ⁱ+a_k–1 (1  i < r).

При этом ^k–1k^r  a₁^k–2(k–1)^r+…+a_k–22^r+a_k–1 .

Доказательство. Проведём индукцию по степени многочлена. Для многочлена первой степени нужно доказать только первое из соотношений, которое следует и в общем случае из условия леммы ( – корень многочлена). При этом очевидно, что указанное в формулировке леммы неравенство тоже выполнено. Столь же просто рассматривается и случай k = 2.

Предположим, что лемма доказана для многочленов степени меньше k и докажем её для многочлена степени k. Поскольку  – корень кратности r–1 для производной многочлена f(x) = kx^k–1 – a₁(k–1)x^k–2 – … – a_k–22x – a_k–1 степени k–1, то запишем соответствующие соотношения для многочлена :

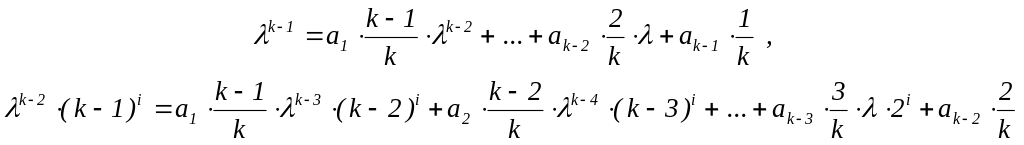
(1  i < r – 1), которые можно записать так:

^k–1k = a₁^k–2(k–1)+…+a_k–22+a_k–1 ,

^k–2(k–1)ⁱk = a₁^k–3(k–2)ⁱ(k–1)+a₂^k–4(k–3)ⁱ(k–2)+…+a_k–332ⁱ+a_k–22

(1  i < r–1).

Первое из этих равенств даёт искомое соотношение при i = 1 для исходного многочлена, а из второй группы равенств получаем:

^k–1k²–^k–1k = a₁^k–2(k–2)(k–1)+a₂^k–3(k–3)(k–2)+…+a_k–3²32+a_k–22 ,

^k–1k² = (a₁^k–2(k–2)(k–1)+a₂^k–3(k–3)(k–2)+…+a_k–3²32+a_k–22)+

+(a₁^k–2(k–1)+a₂^k–3(k–2)+…+a_k–3²3+a_k–22+a_k–1) =

= a₁^k–2(k–1)²+ a₂^k–3(k–2)²+…+ a_k–3²3²+ a_k–22²+a_k–1 .

Это – доказываемое соотношение для исходного многочлена при i = 2. Если эти соотношения уже доказаны при i = 1, 2, … , s < r и s+1 < r, то s < r+1 и можно воспользоваться s-м из доказанных соотношений:

^k–1(k–1)^sk = a₁^k–2(k–2)^s(k–1)+a₂^k–3(k–3)^s(k–2)+…+a_k–3²32^s+a_k–22 

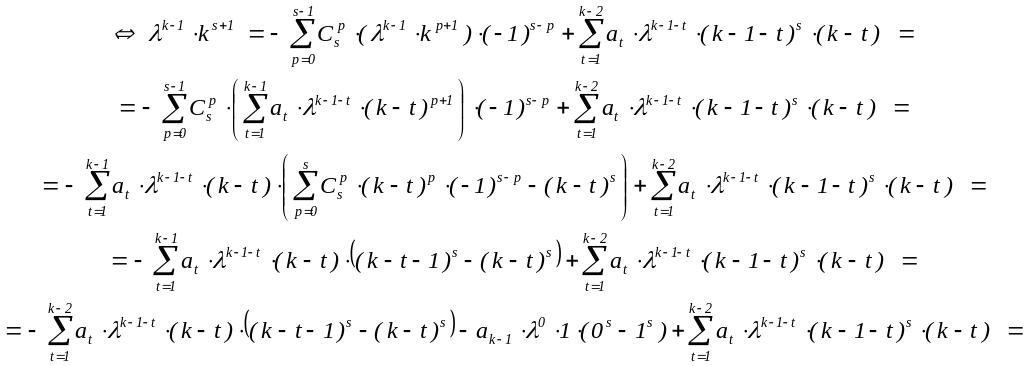
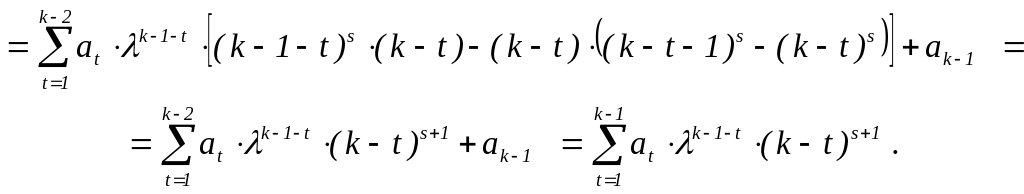
Если предположить, что ^k–1k^r = a₁^k–2(k–1)^r+…+a_k–22^r+a_k–1 , то приведённые выше преобразования, пройденные в обратном порядке, приведут к соотношению

^k–1(k–1)^r–1k=a₁^k–2(k–2)^r–1(k–1)+a₂^k–3(k–3)^r–1(k–2)+…+a_k–3²32^r–1+a_k–22 

Э то противоречит предположению индукции для многочлена .

Лемма доказана.

Эта теорема даёт алгоритм нахождения общего решения линейного рекуррентного соотношения с постоянными коэффициентами