
- •Глава I. Азы комбинаторики
- •§ 1. Основные принципы комбинаторики
- •§ 2. Размещения и перестановки без повторений
- •§ 3. Размещения и перестановки с повторениями
- •§ 4. Подмножества конечных множеств и сочетания
- •§ 5. Сочетания с повторениями
- •§ 6. Принцип включения-исключения
- •§ 7. Примеры решения простейших комбинаторных задач
- •§ 8. Примеры других комбинаторных объектов и сводка некоторых результатов
- •Биномиальные коэффициенты
- •Числа Стирлинга
- •Глава II. Рекуррентные соотношения
- •§ 1. Определение и примеры рекуррентных соотношений
- •Основы метода конечных разностей
- •§ 2. Метод производящих функций для нахождения общего решения линейного однородного рекуррентного соотношения второго порядка
- •Алгоритм нахождения общего решения
- •§ 3. Решение линейных неоднородных рекуррентных соотношений с постоянными коэффициентами и специальной правой частью
- •§ 4. Метод производящих функций для решения общего линейного однородного рекуррентного соотношения с постоянными коэффициентами
- •Алгоритм нахождения общего решения
- •§ 5. Частные решения линейных неоднородных рекуррентных соотношений с постоянными коэффициентами и специальной правой частью
- •§ 6. Некоторые примеры применения производящих функций
§ 7. Примеры решения простейших комбинаторных задач
Подытожим сведения об изученных комбинаторных объектах и их числовых характеристиках в следующей таблице:
Название |
Обозначение |
Количество |
размещение |
|
|
размещение с повторениями |
(b1 ; … ; bs) As |
|
перестановка |
|
Pn = n ! |
перестановка c повторениями |
a1 – k1 раз, … , an – kn раз |
|
подмножество |
{ }, as at при s t |
|B(A)| = 2n |
сочетание |
{ }, as at при s t |
|
сочетание с повторениями |
|
|
На флагштоке поднимается сигнал, содержащий 1, 2 или 3 различных флага из стандартного набора, содержащего 3 флага. Сколько различных сигналов получится (порядок флагов учитывается) ?
Ответ: 15.
Решение. Из одного флага – 3 сигнала, из двух и из трёх флагов – по 6 сигналов. Далее – принцип сложения.
В магазине есть 7 разных видов чашек и 5 различных видов блюдец. Сколькими способами можно купить чашку с блюдцем ?
Ответ: 35-ю способами.
Решение. Типичная задача на принцип умножения. Представим себе, что из города A в город B ведут 7 дорог, на каждой из которых продают разные виды чашек. А из города B в город C ведут 5 дорог, на каждой из которых продают один вид блюдец. Таким образом, чайный набор покупается при проезде из A в C, что можно сделать 35-ю способами.
Монета бросается 10 раз и получается набор длины 10 из выпавших результатов: орёл или решка. Сколько различных наборов с четырьмя орлами получится ?
Ответ:
![]() = 1260.
= 1260.
Сколько слов (произвольных последовательностей) длины 1000 можно составить из букв русского алфавита ?
Ответ: 331000 .
Решение.
В русском алфавите 33
буквы. Так
что
![]() .
.
Простейшая молекула белка, как утверждают учёные-биологи, представляет собой последовательность длины 50 из основных 20-ти аминокислот. Оцените, сколько лет потребуется, чтобы перебрать все возможные комбинации таких последовательностей, если в каждом кубическом миллиметре шарового слоя Земли высоты 10 км. за одну секунду осуществляется независимый перебор 1000000 вариантов ?
Ответ: более 10 21 лет.
Р ешение.
Всего последовательностей длины 50
из 20
аминокислот будет 2050
= 250·1050
.
ешение.
Всего последовательностей длины 50
из 20
аминокислот будет 2050
= 250·1050
.
Объём
шара V
=
![]() ··R3
, поэтому
объём шарового слоя высоты h
вычисляется
так: Vh
=
··[(R
+ h)3
– R3].
Учитывая, что радиус Земли примерно
равен 6400
км., получим
объём рассматриваемого в задаче шарового
слоя
··R3
, поэтому
объём шарового слоя высоты h
вычисляется
так: Vh
=
··[(R
+ h)3
– R3].
Учитывая, что радиус Земли примерно
равен 6400
км., получим
объём рассматриваемого в задаче шарового
слоя
··[64103 – 64003] = ··106·[64,13 – 643] =
= ··106·[0,1·(64,12 + 64,1·64 + 642)]
··105·3·64,12 < 4·4·105·1002 < 1011 (км3).
Далее, 1 км3 = 109 м3 = 109·106 см3 = 1015·103 мм3 . Значит, объём рассматриваемого шарового слоя меньше 1029 мм3.
Даже,
если перебор комбинаций будет вестись
в 1029
мм3,
то одному из этих кубических миллиметров
нужно перебрать не менее
![]() = 250·1021
= 250·1021
![]() 1015·1021
= 1036
комбинаций.
1015·1021
= 1036
комбинаций.
В
одном году менее 60·60·24·366
< 100·100·100·1000 = 109
секунд.
Значит, понадобится более
![]() = 1027
лет. Учитывая,
что в каждую секунду производится
перебор 106
вариантов,
время перебора сокращается до 10
21 лет.
= 1027
лет. Учитывая,
что в каждую секунду производится
перебор 106
вариантов,
время перебора сокращается до 10
21 лет.
А как же возраст Вселенной, оцениваемый учёными-астрофизиками в 20 миллиардов лет (20·109 = 2·1010 лет) ?! Могла ли случайная эволюция за это время создать не только простейшую молекулу белка, но и гораздо более сложные структуры ? Например, геном человека, как утверждают те же учёные-биологи, является последовательностью из 25000 генов, а каждый ген сам обладает сложной структурой ! Думайте сами, решайте сами…
Каждую клетку таблицы 33 можно раскрасить в 3 цвета. Сколькими способами можно раскрасить таблицу, чтобы в каждой строке и в каждом столбце встречались все три цвета ?
Ответ: 12.
Решение. Для определённости обозначим цвета клеток средней строки буквами б, с, к. Тогда нетрудно понять, что возможны только следующие два варианта раскраски таблицы:
к |
б |
с |
|
с |
к |
б |
б |
с |
к |
|
б |
с |
к |
с |
к |
б |
|
к |
б |
с |
Учитывая, что допускаются произвольные перестановки цветов, т.е. вместо порядка (б, с, к) можно рассматривать произвольный другой порядок – перестановку этих букв, получим 23 ! = 12 раскрасок.
Сколько можно сшить трёхцветных флагов из полосок материи шести цветов, если флаги с одинаковыми цветами, но различными их расположениями считать разными ?
Ответ:
![]() = 120.
= 120.
Решение.
Типичная задача на размещения шести
элементов по трём местам. А если не
учитывать расположение полос ? Тогда
![]() = 20.
= 20.
В стране 30 городов, каждые два из которых соединены авиалиниями. Сколько всего авиалиний ?
Ответ:
![]() = 435.
= 435.
Решение.
Авиалиния определяется своими концами,
т.е. произвольно выбранными двумя
городами из 30.
Число этих сочетаний равно
![]() = 435
.
= 435
.
Игральный кубик бросают шесть раз. Сколько последовательностей из шести результатов бросаний содержат хотя бы одну шестёрку ?
Ответ: 21031.
Решение. Проще вычислить, в скольких случаях совсем нет шестёрки. Это произойдёт в 56 случаях из общего числа 66 случаев. Таким образом, хотя бы одна шестёрка выпадает в 66 – 56 = (62)3 – (52)3 = (62–52)(64+6252+54) = = 11((62+52)2–6252) = 11(61+30)(61–30) = 119131 = 91341 = 90341+341= = 30690 + 341= 31031 случаях.
Сколько четырёхзначных чисел можно составить из цифр 0, 3, 5, 8 (цифры не повторяются) ?
Ответ: 18.
Решение. P4 – P3 = 4 ! – 3 ! = 18 (учесть, что 0 не может быть старшей цифрой).
Замечание. Если цифры могут повторяться, то получится 3·43 = 192 числа. Если исключать число 0 = 0000, то останется 191 число.
У математика 7 книг, а у поэта – 9. Сколькими способами можно обменять две математические книги на четыре поэтических ?
Ответ: 15876.
Решение.
Правило умножения:
![]() =
21756
= 15876.
=
21756
= 15876.
Сколько различных (в том числе и бессмысленных) слов можно составить из букв слов ТИГР, ПАРА.
Ответ: 24, 12.
Решение.
Для слова
ТИГР,
в котором нет одинаковых букв, ответ
4! = 24.
Для слова ПАРА
–
![]() = 12: ПАРА,
ПРАА, ПААР, АПРА, АРПА, ААРП, АПАР,
ААПР, АРАП, РПАА, РАПА, РААП. Здесь
две буквы А
можно менять
местами, поэтому и делим на количество
перестановок на двух символах.
= 12: ПАРА,
ПРАА, ПААР, АПРА, АРПА, ААРП, АПАР,
ААПР, АРАП, РПАА, РАПА, РААП. Здесь
две буквы А
можно менять
местами, поэтому и делим на количество
перестановок на двух символах.
Для
слова ПАРАЛЛЕЛОГРАММ,
в котором три буквы А
и Л,
по две буквы Р
и М
аналогично
получим
![]() = 605404800.
= 605404800.
Сколько всего результатов бросания трёх одинаковых игральных костей ?
Ответ: 56.
Решение.
Сочетания
с повторениями: результат бросания
представляет собой набор
![]() ,
где
,
где
![]() .
Поэтому количество результатов равно
.
Поэтому количество результатов равно
![]() .
.
Карточная колода из 52 карт раздаётся 4-м игрокам: вначале 13 карт первому, потом – 13 карт второму, и т.д. В скольких случаях каждому из игроков будет роздано по тузу ?
Ответ:
134![]() 12!4!
.
12!4!
.
Решение.
Рассматриваем
колоду как слово из 52
различных
букв. Если один из тузов, например, туз
червей (Ч),
попал в первые 13
букв, то он
может оказаться на любой позиции с 1-й
по 13-ю,
а на остальных позициях могут участвовать
все буквы, кроме тузов, без повторений,
т.е.
![]() . Всего вариантов (по принципу сложения)
13
.
. Всего вариантов (по принципу сложения)
13
.
Для
второго игрока и туза бубён (Б)
ситуация аналогична, только уже нельзя
использовать карты первого игрока:
количество вариантов 13![]() . Для третьего и туза пик (П)
– 13
. Для третьего и туза пик (П)
– 13![]() , а для четвёртого и трефового туза (Т)
– 13
, а для четвёртого и трефового туза (Т)
– 13![]() = 1312!
.
= 1312!
.
По
принципу умножения получаем 134![]()
![]()
![]() 12!
. В этих
вычислениях был фиксирован порядок
тузов: (Ч, Б,
П, Т). Ясно,
что возможны любые перестановки. Так
что ответ: 134
12!4!
.
12!
. В этих
вычислениях был фиксирован порядок
тузов: (Ч, Б,
П, Т). Ясно,
что возможны любые перестановки. Так
что ответ: 134
12!4!
.
Сколько существует автобусных билетов с шестизначными номерами, в которых участвуют только цифры 3, 5, 7, и сумма цифр которых делится на 3 ?
Ответ: 213.
Решение.
Общее число автобусных билетов с цифрами
3, 5, 7
подсчитать легко: это просто
![]() = 36.
Какие из номеров билетов делятся на 3
? Те, сумма
цифр которых делится на 3.
Цифру 3 при
этом, очевидно, можно не учитывать. Если
в номере участвуют k
пятёрок и
m
семёрок, то
их сумма k5+m7
= k(5+7)+(m–k)7
делится на
3 тогда
и только тогда, когда делится на 3
разность
m–k.
Можно перечислить все варианты:
= 36.
Какие из номеров билетов делятся на 3
? Те, сумма
цифр которых делится на 3.
Цифру 3 при
этом, очевидно, можно не учитывать. Если
в номере участвуют k
пятёрок и
m
семёрок, то
их сумма k5+m7
= k(5+7)+(m–k)7
делится на
3 тогда
и только тогда, когда делится на 3
разность
m–k.
Можно перечислить все варианты:
троек |
пятёрок |
семёрок |
число билетов |
6 |
0 |
0 |
1 |
0 |
6 |
0 |
1 |
0 |
0 |
6 |
1 |
3 |
3 |
0 |
|
3 |
0 |
3 |
= 20 |
0 |
3 |
3 |
|
4 |
1 |
1 |
2 |
1 |
4 |
1 |
= 15 |
1 |
1 |
4 |
= 15 |
2 |
2 |
2 |
|
Всего получается 1+2·20+2·1+30+2·15+90+20 = 213 билетов.
Доказать равенство
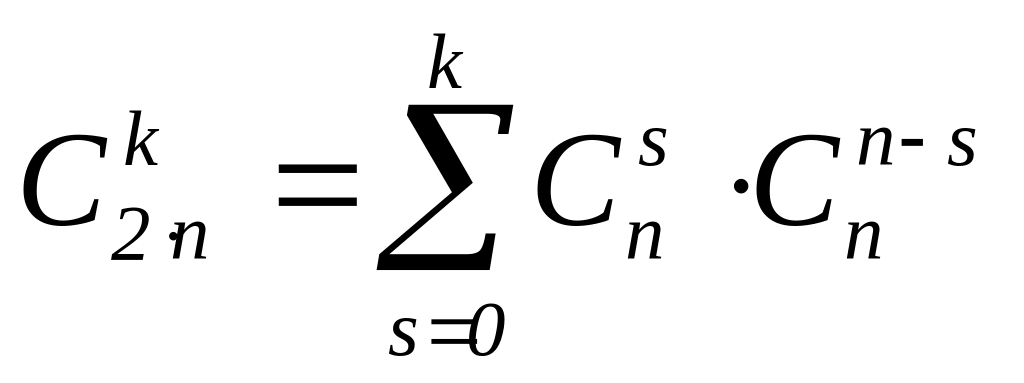 .
.
Решение. По формуле бинома Ньютона имеем
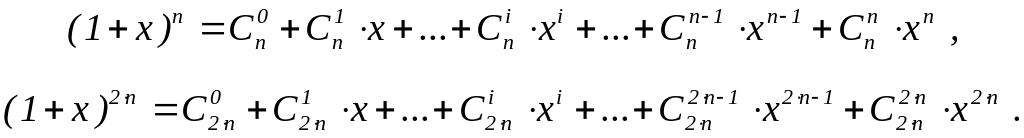
Отсюда
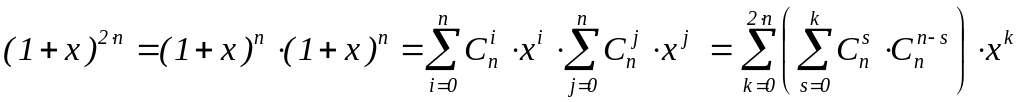 .
С другой стороны, как было отмечено
выше,
.
С другой стороны, как было отмечено
выше,
![]() .
Сравнивая коэффициенты при одинаковых
степенях x,
получим требуемое равенство.
.
Сравнивая коэффициенты при одинаковых
степенях x,
получим требуемое равенство.
Вычислить сумму “арифмо-геометрической” прогрессии
1 + 2q + 3q2 + … + (n+1)qn .
Ответ:
![]() при q
= 1,
при q
= 1,
![]() при q
1.
при q
1.
Решение. Дифференцируя формулу суммы геометрической прогрессии
1
+ x
+ … + xn+1
=
![]() (x
1),
(x
1),
получим
1+2x+…+(n+1)xn
=
![]() .
.
Для правильной записи ответа нужно учесть случай q = 1.
