3. Гідростатика

Гідростатика – розділ гідравліки, у якому вивчаються закони рівноваги рідин, а також твердих тіл, цілком чи частково занурених у рідину.

3.1. Тиск у крапці спочиваючої рідини

В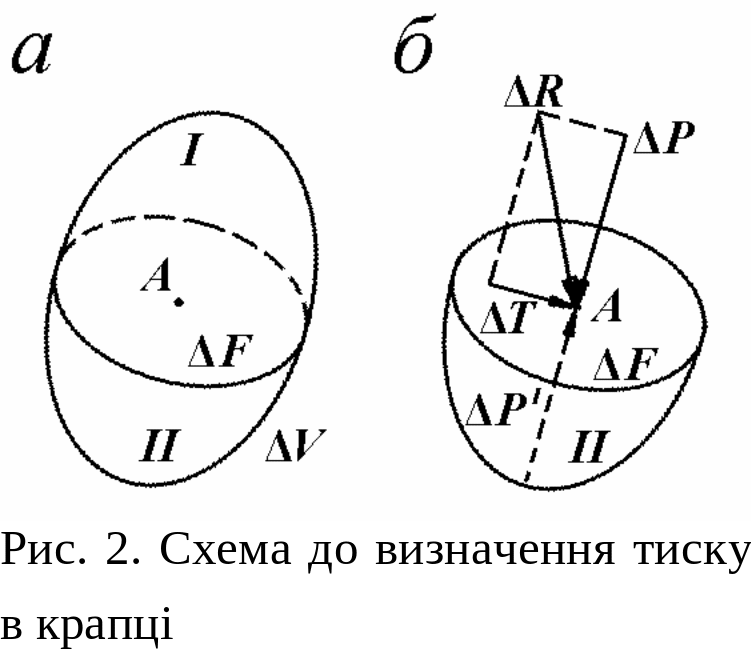 иділимо навколо крапки , що знаходиться усередині спочиваючої рідини, елементарний об'єм рідини і розсічемо його на дві частини довільною площиною, проведеною через крапку (рис. 2, а). Відкинемо одну з частин цього об'єму і для того, щоб частина, що залишилася, знаходилася в рівновазі, замінимо дію відкинутої частини на площадку розподіленими по ній елементарними поверхневими силами.

Припустимо, що рівнодіюча цих елементарних сил діє в напрямку, показаному на рис. 2, б. Розкладемо на дві складові: – лежачу в площині перетину і – нормальну до цієї площини.

Очевидно, що в спочиваючих ньютонівських рідинах дотична складова , тому що в противному випадку вона викликала би зрушення часток уздовж площини розділу. Складова , спрямована по внутрішній нормалі до площини розділу, є стискаючої і її дія зустрічає з боку рідини рівне і протилежно спрямовану протидію , завдяки чому рівновага рідини не порушується.

Значення середньої напруги стиску чи середнього тиску рідини на елементарну площадку буде дорівнювати відношенню до , тобто . Зменшуючи площадку навколо крапки так, щоб її величина прагнула до нуля, одержимо тиск у крапці спочиваючої рідини, чи гідростатичний тиск,

(22)

Таким чином, елементарна сила тиску, що діє на нескінченно малу площадку , може бути підрахована як .

Тиск у крапці спочиваючої рідини володіє двома основними властивостями.

Перша властивість. Тиск у крапці спочиваючої рідини завжди нормально до поверхні (площадці), що сприймає цей тиск. Це властивість не вимагає доказу, тому що воно очевидно зі сказаного вище про силу .

Друга властивість. Тиск у крапці спочиваючої рідини у всіх напрямках однаково за значенням, тобто є скаляром.

Д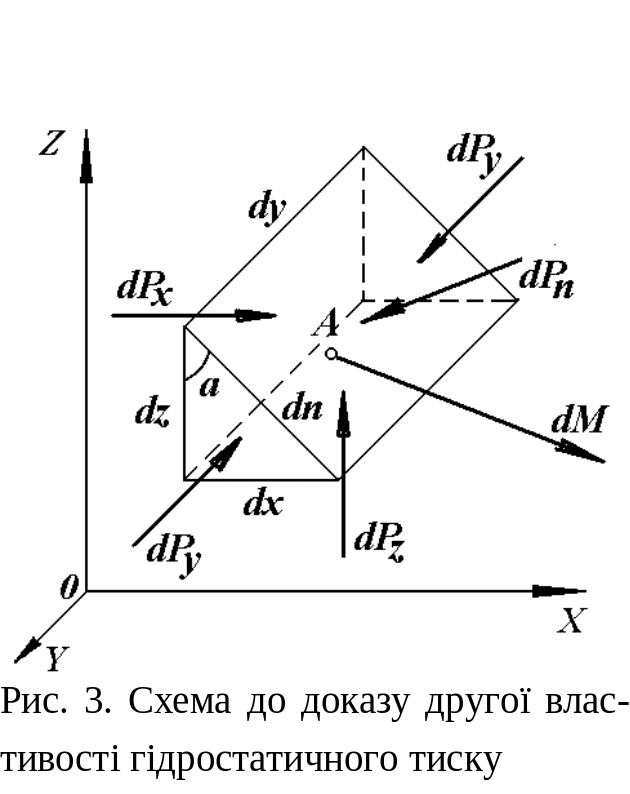 ля доказу цієї властивості візьмемо в рідині, що знаходиться в рівновазі, крапку і виділимо навколо її нескінченно малий обсяг рідини у виді трикутної призми (рис. 3) з ребрами , , , , причому кут нахилу ребра до ребра узятий довільним.

Відкинемо думкою всю навколо призми рідину, а для збереження рівноваги прикладемо до кожної грані відповідні елементарні сили гідростатичного тиску , , і т.ін., що, як було зазначено вище, діють нормально до граней і будуть спрямовані усередину розглянутого об'єму. Крім цих поверхневих сил на рідину, що знаходиться усередині призми, діють ще масові сили, результуюча яких прикладена в центрі ваги обсягу й у загальному випадку дорівнює , де – результуюче прискорення масових сил,

проекції якого на координатні осі: , , .

Користуючись принципом затвердіння, відповідно до якого рівновага рідкого тіла не порушиться, якщо припустити його затверділим, застосуємо до виділеного об'му закони механіки твердого тіла – спроектуємо діючі на нього сили на координатні осі і дорівняємо суми проекцій на відповідні осі нулю. На вісь чи , але оскільки , то , чи після скорочення на , відкіля , тому що останнім членному через його малість можна зневажити. На вісь чи , але оскільки , то , чи після скорочення на , відкіля , тому що останнім членному через його малість можна зневажити.

Оскільки і порізно рівні , то вони рівні і між собою, а тому що кут був обраний довільно, те і у всіх інших напрямках значення гідростатичного тиску буде однаково

(1.23)