Свойства определенного интеграла.

В этой статье мы перечислим основные свойства определенного интеграла. Большинство этих свойств доказываются на основе понятий определенного интеграла Римана и Дарбу. Вычисление значения определенного интеграла очень часто проводится с использованием первых пяти свойств, так что мы будем при надобности на них ссылаться. Остальные свойства определенного интеграла, в основном, применяются для оценки различных выражений. Основные свойства определенного интеграла. Условимся, что a < b.

1. Для функции y = f(x), определенной при x = a, справедливо равенство  . То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма   для любого разбиения промежутка [a; a] и любого выбора точек   равна нулю, так как 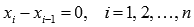 , следовательно, пределом интегральных сумм является ноль.

2. Для интегрируемой на отрезке [a; b] функции выполняется  . Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b.

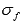3.  для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x). Доказательство. Запишем интегральную сумму функции   для данного разбиения отрезка и данного выбора точек  :   где   и   - интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно. Переходя к пределу при   получим  , что по определению интеграла Римана равносильно утверждению доказываемого свойства.

4. Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке [a; b] функции y = f(x) и произвольного числа k справедливо равенство  . Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:

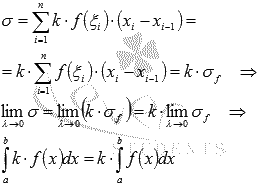
5. Пусть функция y = f(x) интегрируема на интервале X, причем   и  , тогда  . Это свойство справедливо как для  , так и для   или  . Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.

6. Если функция интегрируема на отрезке [a; b], то она интегрируема и на любом внутреннем отрезке  . Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.

7. Если функция y = f(x) интегрируема на отрезке [a; b] и   для любого значения аргумента  , то 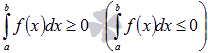 . Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек   при   будет неотрицательной (не положительной). Следствие. Для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x) справедливы неравенства:   Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.

Вообще 11 свойств

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x₀ < x₁ < x₂ < x_n = b Тогда говорят, что произведено разбиение R отрезка [a;b] Далее выберем произв. точку  , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм Θ_R при  , если он существует независимо от разбиения R и выбора точек ξ_i, т.е.   (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

• 

• a – нижний предел.

• b – верхний предел.

• f(x) – подынтегральная функция.

• λ_R - длина частичного отрезка.

• σ_R – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R.

• λ_R - максимальная длина част. отрезка.

Определение интеграла на языке  , δ:(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λ_R < δ, выполняется неравенство: |I- σ_R | = |∑^n-1_i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫_a^bf(x)dx