11 Понятие функции. Элементарные функции

Функции и способы их задания

Назовем упорядоченной парой (x, y) двухэлементное множество

{x, y}, в котором элемент x находится на первом месте, а элемент y – на

втором. Элемент x называется первой координатой упорядоченной пары, а

элемент y – второй координатой. Две упорядоченные пары равны, когда

совпадают их координаты: (x, y)  (u,v)  x  u, y  v .

Функцией f называется множество упорядоченных пар чисел (x, y),

таких, что x  X , y Y и каждому элементу x  X ставится в

соответствие единственный элемент y Y . Обозначение: f: X → Y.

Рис. 1.1

Например, соответствия f и g, изображенные на рисунке 1.1 а и б,

являются функциями, а на рисунке 1.1 в и г – нет. В случае в – не каждому

элементу x  X соответствует y Y . В случае г не соблюдается условие

однозначности.

Множество X называется областью определения функции f, а

множество Y – областью значений. Обозначают: Df и Ef

. Если ясно, какие

множества X и Y имеются в виду, то пишут y  f (x). Элемент x называется

аргументом (независимой переменной), а y – значением (зависимой

переменной) функции f.

Пример. Найти область определения и область значений функции у= х2+ 1

Решение. Областью определения функции является множество Df = (–∞, ∞), область значений является множество Ef = [0, ∞).

Пример. Найти область определения и область значений функции у= х2+ 1

Решение. Областью определения функции является множество Df = (–∞, ∞), область значений является множество Ef = [0, ∞)

12 Признаки существования предела (для последовательностей)

Признаки существования предела

1. Если   и  , то 

2. Монотонная и ограниченная последовательность имеет предел.

3. Числовая последовательность (x_n) имеет конечный предел тогда и только тогда, когда

(критерий Коши).

Число e

Последовательность  , имеет конечный предел, называемый числом е:

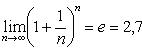
13 Дифференциал функции. Свойства дифференциала

Дифференциа́л (от лат. differentia — разность, различие) — линейная часть приращения функции.

Свойства

• Матрица линейного оператора   равна матрице Якоби; её элементами являются частные производные f.

  • Отметим, частные производные могут быть определены в точке, где дифференциал не определён.

• Дифференциал функции f связан с её градиентом   следущим определяющим соотношением

• Дифференциал функции f связан с производной по направлению следущим определяющим соотношением

14 Производная экономический смысл производной Определение

Пусть в некоторой окрестности точки   определена функция   Производной функции называется такое число  , что функцию в окрестности U(x₀) можно представить в виде

f(x₀ + h) = f(x₀) + Ah + o(h)

если   существует.

 экономический смысл производной.

Издержки производства y будем рассматривать как функцию количества выпускаемой продукции x. Пусть /\ x - прирост продукции, тогда /\ y -приращение издержек производства и /\ y / /\ x - среднее приращение издержек производства на единицу продукции.

Производная

			/\ y
y'	=	lim	-----
		/\x -> 0	/\ x

выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.

Предельные издержки зависят от уровня производства (количества выпускаемой продукции) и определяются не постоянными производственными затратами, а лишь переменными (на сырье, топливо и т.п.). Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность, предельная производительность и другие предельные величины.

Применение дифференциального исчисления к исследованию экономических объектов и процессов на основе анализа этих предельных величин получило название предельного анализа. Предельные величины характеризуют не состояние (как суммарная или средняя величины), а процесс изменения экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Следует учесть, однако, что экономика не всегда позволяет использовать предельные величины в силу неделимости многих объектов экономических расчетов и прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). Вместе с тем в ряде случаев можно отвлечься от дискретности показателей и эффективно использовать предельные величины.

Рассмотрим в качестве примера соотношения между средним и предельным доходом в условиях монопольного и конкурентного рынков.

Суммарный доход (выручку) от реализации продукции r можно определить как произведение цены единицы продукции p на количествопродукции q, т.е. r = pq.

В условиях монополии одна фирма полностью контролируют предложение определенной продукции, а следовательно, цены на них. При этом, как правило, с увеличением цены спрос на продукцию падает. Будем полагать, что это происходит по прямой, т.е. кривая спроса p(q) - есть линейная убывающая функция p = aq + b, где a > 0, b < 0. Тогда суммарный доход от реализованной продукции составит r = (aq + b) = aq² + bq. В этом случае средний доход на единицу продукции r_ср = r/q = aq + b, а предельный доход составит r'_q = 2aq + b. Следовательно, в условиях монопольного рынка с ростом количества реализованной продукции предельный доход снижается, что приводит к уменьшению (с минимальной скоростью) среднего дохода.

В условиях совершенной конкуренции, когда число участников рынка велико, и каждая фирма не способна контролировать уровень цен, устойчивая продажа товаров возможна по преобладающей рыночной цене, например, p = b. При этом суммарный доход составит r = qb и соответственно средний доход r_ср = r/q = b и предельный доход r'_q = b. Таким образом, в условиях свободного конкурентного рынка средний и предельный доходы совпадают.