1
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально, под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.
Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а, также, описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).
Предел фу́нкции — одно из основных понятий математического анализа.
2
Основные неопределенности пределов и их раскрытие.
С непосредственным
вычислением пределов основных
элементарных функций разобрались.
При
переходе к функциям более сложного вида
мы обязательно столкнемся с появлением
выражений, значение которых не определено.
Такие выражения
называют неопределенностями.
Перечислим
все основные
виды неопределенностей:
ноль делить на ноль 
(0
на 0),
бесконечность делить на бесконечность 
,
ноль умножить на бесконечность 
,
бесконечность минус бесконечность 
,
единица в степени бесконечность 
,
ноль в степени ноль 
,
бесконечность в степени ноль 
.
ВСЕ
ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ
НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ
КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Раскрывать
неопределенности позволяет:
упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
использование замечательных пределов;
применение правила Лопиталя;
использование замены бесконечно малого выражения ему эквивалентным (использование таблицы эквивалентных бесконечно малых).
Пример.
Вычислить
предел 
Решение.
Подставляем
значение:
И
сразу получили ответ.
Ответ: 
3
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
4 Производная физический смысл производной (в конспектах)
Произво́дная — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции. Физический смысл производной — скорость изменения величины или процесса
5 производная геометрический смысл производной
Смотри Туда ^^^^^^^^^^^^^^^^^
Рассмотрим график функции y = f ( x ):
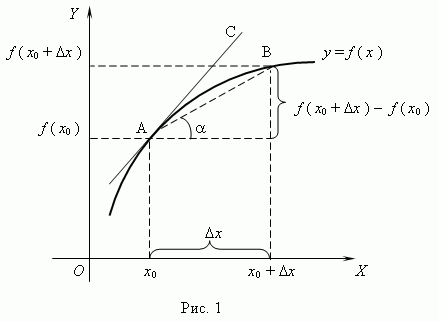
Из
рис.1 видно, что для любых двух
точек A и B графика
функции: 
xf(x0+
x)−f(x0)=tg
,
где 
-
угол наклона секущейAB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей.
Если
зафиксировать точку A и
двигать по направлению к ней точку B,
то 
x неограниченно
уменьшается и приближается к 0, а
секущая АВ приближается
к касательной АС.
Следовательно,
предел разностного отношения равен
угловому коэффициенту касательной в
точке A.
Отсюда
следует:
производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
6 БМВ Свойства БМВ
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.