19 Способы вычисления интеграла

Метод замены переменных:

∫f(x)dx=∫f(φ(t))·φ`(t)dt → x=φ(t)

∫sin 5x dx=∫sin t 1/5dt=1/5∫sin t dt=-1/5 cost+C =-1/5cos 5x+C

5x=t; x=1/5t; dx=1/5 dt

35 Интегрир-ие по частям:

∫ U·dV=UV-∫VdU

Возможности применения связаны с тем, что дифференцир-ие может существенно упростить один из сомножителей (при условии что дифф-ие не слишком усложнит другой)

∫ x²·sinx dx

x²=U dU=2x dx

sin x dx =dV V=-cos x

∫ = x²·sin x dx=-x²·cos x -∫(-cos x)2x dx=-x²·cos x+2∫x·cos x dx

x=U dU=dx

cos x dx=dV V=sin x

∫ = x²·sin x dx=-x²cos x +2(x·sin x-∫sin x dx)= -x²·cos x+2x·sin x +2cos x+C

36 Рациональной дробью называется ф-ия, равная отношению двух многочленов f(x)=Pm(x)/Qn(x), Pm(x)-многочлен степени m, Qn(x)- многочлен степени n.

Рациональная дробь наз. правильной если степень числителя меньше степени знаменателя, т.е. m<n, в противном случае дробь неправильная.

Интегрирование дробей методом разложения на элементарные дроби:

1 Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби.

2 Разложив знаменатель дроби на множители, представить её в виде суммы простейших рац. дробей.

3 Проинтегрировать многочлен и полученную сумму простейших дробей.

20 Приложение определенного интеграла. Определение обьема тела вращения

Объёмы тел вращения.

13.4.1. Вычисление объёма тела по площадям поперечных сечений. Пусть тело V расположено в пространстве между плоскостями x = a и x =b, и для   известна площадь его поперечного сечения S = S(x). Требуется определить объём этого тела.   Рассечём это тело плоскостями x = x₀ = a, x = x₁, x = x ₂, …, x = x_i-1, x = x_i, …, x = x _n-1, x = x_n = b на n слоёв (a = x₀< x₁ < < x₂< …< x_n-1 < x_n= b), на каждом из отрезков [x_i-1, x_i] возьмём произвольную точку  ; будем считать, что объём слоя, заключенного между плоскостями x = x_i-1 и x = x_iприближённо равен объёму   цилиндрика с площадью основания   и высотой  :  . Сумма объёмов   - объём ступенчатой фигуры - при   стремится к искомому объёму V, поэтому  . 13.4.2. Объём тела, получающегося при вращении кривой вокруг координатной оси. Если объём Vполучается в результате вращения кривой y = f(x),  , вокруг оси Ox, то, очевидно,  , поэтому  .  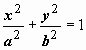Пример: найти объём эллипсоида, получающегося при вращении эллипса   вокруг оси Ox.  Решение: эту задачу проще решить, если применить параметрические уравнения эллипса:  . Верхняя дуга эллипса получается при изменении t от 0 до  , при этом точке крайней левой точке эллипса соответствует значение параметра t₀ , равное  , крайней правой точке соответствует значение t_k = 0. Формула   для кривой, заданной параметрически,примет вид  , поэтому  .  Если требуется найти объём тела, которой получается при вращении плоской фигуры ABCD вокруг оси Oy, рассуждаем по другому. Разбиваем тело на полые цилиндры радиуса x, толщины  , высоты f(x). Объём этого цилиндра равен произведению длины окружности   на толщину   и высоты f(x); суммируя эти объёмы и переходя к пределу при  , получим  .  13.4.3. Объём тела, получающийся при вращении сектора, ограниченного кривой   и двумя полярными радиусами   и  , вокруг полярной оси находится по формуле 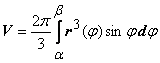 .  Пример: найти объём тора, полученного вращением окружности   вокруг полярной оси.  Решение: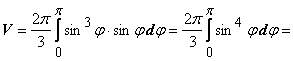   

21 Определенный интеграл и его свойства

Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.

     Теорема 1. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], то

т. е. интеграл суммы равен сумме интегралов слагаемых.

     В самом деле, составляя интегральную сумму для функции f(x) + g(x), очевидно, будем иметь

после чего остается перейти к пределу при λ → 0.

     Аналогично доказывается

     Теорема 2. Если f(x) - непрерывная функция, а c - постоянное число, то

т. е. постоянный множитель можно выносить за знак интеграла.

     Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.

     В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = x_m, то

     Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0.