Ширина спектра сигналов

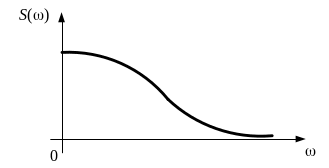
Рис.1.21

На рисунке 1.21 приведен график амплитудно-частотного спектра, произвольно выбранного некого одиночного сигнала, причем модуль спектральной плотности монотонно убывает с ростом значения частоты.

Для большинства одиночных сигналов характерно такое распределение модуля спектральной плотности от частоты.

Вычислив интегралы

,

получим значения, пропорциональные соответственно полной энергии сигнала W₀, и энергии сигнала W(ω), сосредоточенной в полосе частот от 0 до .

Отношение

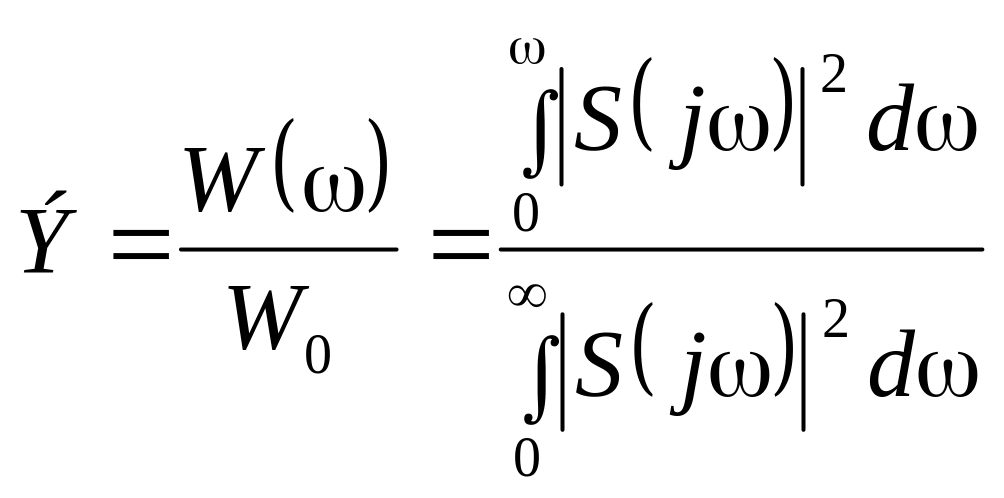
показывает, какая часть всей энергии сигнала сосредоточена в диапазоне частот от 0 до .

Шириной спектра сигнала со сплошным спектром называют область частот (от 0 до или от до ), в пределах которой заключена основная часть (принята величина 90 %) энергии сигнала.

Рис.1.22

На рисунке 1.22 показан амплитудно-частотный спектр некого периодического сигнала, причем амплитуды спектральных составляющих монотонно или немонотонно убывают с ростом частоты.

Энергия сигналов, обладающих дискретным спектром, пропорциональна:

,

где  постоянная составляющая;  действующее значение k-й составляющей.

Если вычислить

,

получим значение, пропорциональное энергии сигнала в полосе частот от 0 до некоторой частоты .

Отношение

показывает, какая часть энергии сигнала с дискретным спектром сосредоточена в диапазоне частот от 0 до .

Шириной спектра сигналов с дискретным спектром называют область частот (от 0 до или от до ), в пределах которой заключена основная часть (не менее 90%) энергии сигнала.

Сравнивая определения ширины спектра сигналов со сплошным спектром и с дискретным спектром, можно заметить отличие ("90% и не менее 90%"), обусловленное дискретным характером изменения величины .

Спектры видеосигналов сосредоточены в области низких частот, радиосигналов – в области частот несущего колебания.

Важнейшей характеристикой сигналов в радиотехнике является база сигнала (коэффициент широкополостности), равная произведению длительности сигнала (τ_с) на ширину его спектра (Δƒ_с) n=τ_cΔf_c.

Сигналы, у которых база сигнала порядка 1, называют простыми (узкополосными) сигналами. К простым сигналам относят одиночные и периодические последовательности импульсов без внутриимпульсной модуляции.

У сложных (широкополосных) сигналов сложными сигналами являются радиосигналы с внутриимпульсной частотной или фазо-кодовой модуляцией, а также, пачки видео и радиоимпульсов.

1.2. Одиночные сигналы и их спектры

1.2.1. Одиночные видеосигналы и их спектры

Рассмотрим спектры некоторых простейших видеосигналов.

Спектр дельта-функции

Дельта-функцией называется сигнал вида (рис. 1.23):

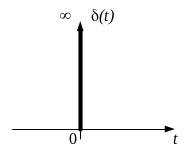
Рис. 1.23

Спектральную плотность получим путем вычисления интеграла

.

Такой результат является следствием так называемого фильтрующего свойства дельта-функции(1.24), которое заключается в следующем

, т. к. , то ,

поэтому , .

График спектра показанный на рисунке 1.25. Амплитудно-частотный спектр на всех частотах одинаков и равен 1. Фазо-частотный спектр на всех частотах равен 0. АЧС является сплошным и ширина спектра бесконечна.

Рис.1.24

Рис.1.25

Начальные фазы всех гармонических колебаний (рис. 1.26) одинаковы и равны 0. Это значит, что в момент времени = 0 все составляющие, изменяющиеся по косинусоидальному закону, проходят через амплитудное значение. В этот момент их сумма образует бесконечную величину.

Рис.1.26