Сигналы в спектральной области

Аналитическое или графическое представление сигналов как функции частоты является представлением сигналов в спектральной (частотной) области.

Различают представление сигналов в спектральной области с дискретным и сплошным спектрами.

Можно доказать, что периодические сигналы обладают дискретными спектрами, а одиночные и пачечные сигналы – сплошными.

Пусть некоторый периодический сигнал представлен совокупностью u(t) гармонических колебаний:

.

Совокупность частот представленных колебания является частотным спектром данного сигнала.

Совокупность амплитуд на соответствующих частотах

…

является амплитудно-частотным спектром данного сигнала.

Совокупность начальных фаз на соответствующих частотах

…

...

является фазо-частотным спектром данного сигнала.

Амплитудно-частотный спектр (АЧС) (рис. 1.19) и фазо-частотный спектр (ФЧС) (рис. 1.20) могут быть изображены в виде системы, состоящей из двух графиков.

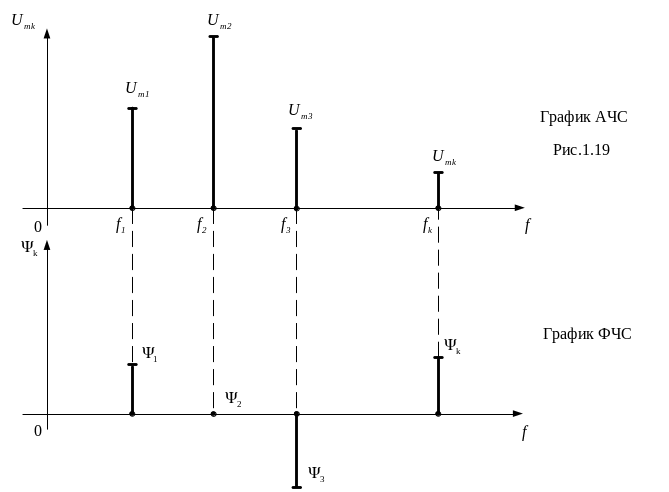
Рис. 1.20

Для одиночных и пачечных сигналов АЧС и ФЧС будут сплошными.

Для расчета спектров, т.е. для представления сигналов как функции частоты, используют следующие основные приемы:

• тригонометрические преобразования,

• интегральное преобразование Фурье,

• разложение в ряд Фурье.

В результате интегрального преобразования Фурье вычисляют спектральную плотность заданного одиночного сигнала и представляют ее в показательной форме записи

,

здесь – спектральная плотность, – модуль спектральной плотности, – аргумент спектральной плотности, – сигнал.

Аналитические выражения или , а так же или являются зависимости, описывающими АЧС и ФЧС данного сигнала.

В результате разложения в ряд Фурье представляют заданный периодический сигнал в виде совокупности гармонических составляющих:

,

где – частота гармонической составляющей с номером , - постоянная составляющая, – амплитуда гармонической составляющей с номером K, – начальная фаза гармонической составляющей с номером .

Расчет и проводится согласно выражению

,

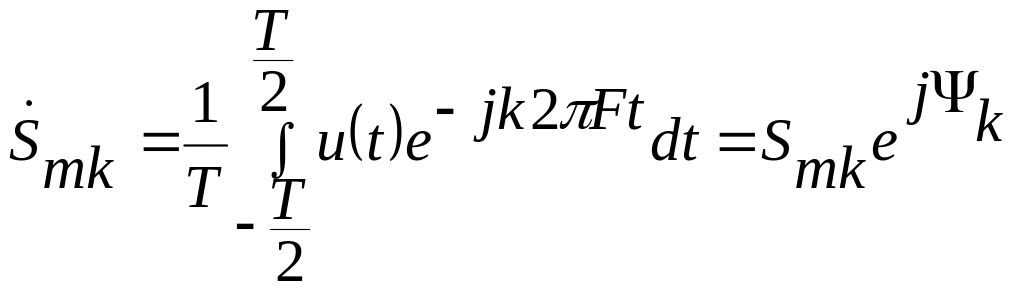где - комплексная амплитуда ряда Фурье.

Расчет проводится аналогично, при :

Между спектральной плотностью и комплексной амплитудой ряда Фурье существует связь:

, ,

которая позволяет, зная значения спектральной плотности, вычислить комплексную амплитуду ряда Фурье путем вычисления спектральной плотности на частотах и умножения полученных значений на множитель .

Свойства преобразований Фурье

При спектральном анализе сигналов объем математических преобразований в ряде случаев можно существенно сократить, если использовать следующие свойства преобразований Фурье.

• Свойство аддитивности

Если ≓ , ≓ , ≓ , ..., ≓ , то для ≓ .

• Свойство однородности

Если ≓ , то для ≓ , где - постоянный множитель.

• Свойство сдвига аргумента

Если ≓ , то

≓

• Свойство смещения

Если ≓ , то ≓

• Свойство дифференцирования

Если ≓ , то ≓

• Свойство интегрирования

Если ≓ , то ≓