Центр тяжести
1. ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ЦЕНТРОВ ТЯЖЕСТИ.
Центром тяжести тела называют центр системы параллельных сил. которую приближенно образуют силы тяжести его элементарных частиц.
Радиус-вектор центра тяжести тела вычисляем как радиус-вектор центра параллельных сил по формуле:
(1)
где
- радиус-вектор точки приложения силы
тяжести элементарной части тела, принятой
за точку;
-
сила
тяжести элементарной частицы;
,
- сила
тяжести всего тела;
n-число
частей, на которое мысленно разбито все
тело. Центр тяжести является точкой
приложения равнодействующей силы
тяжести, если силы тяжести
отдельных его частей считать системой
параллельных сил.
Если в (1) перейти к пределу,
увеличивая число элементарных частей
n
до бесконечности,
то после замены
дифференциалом
dP,
а суммы - интегралом получим:
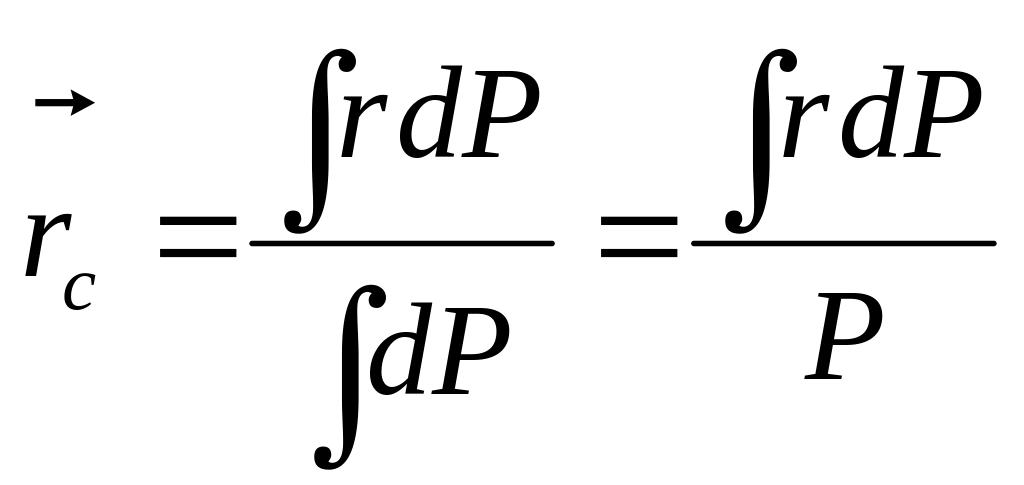(1’)
где
- радиус-вектор
элементарной части тела, принятой за
точку. В проекциях на оси
координат из (1) и (1’) получаем:
,
,
,
,
,
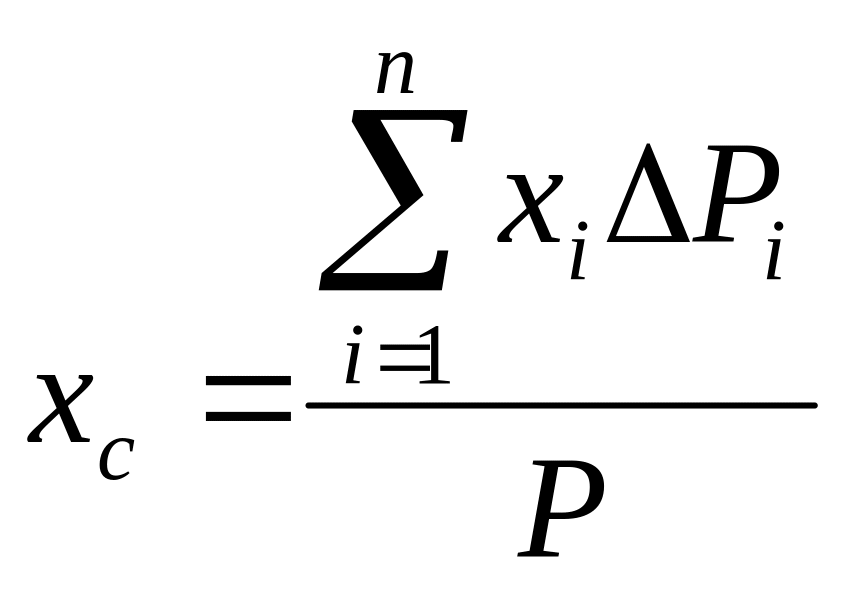где
,
,
- координаты центра тяжести:
,
,
- координаты точки приложения
силы тяжести
Используя понятие центр
тяжести тела, введем понятие его центра
масс. Силы тяжести
элементарных частей тела можно выразить
через их массы
.
и
М и ускорение
силы тяжести g
с помощью формул
Подставляя эти значения сил тяжести в (1) и (1*) после сокращения на g, которое принимаем одинаковым для всех частей тела, имеем
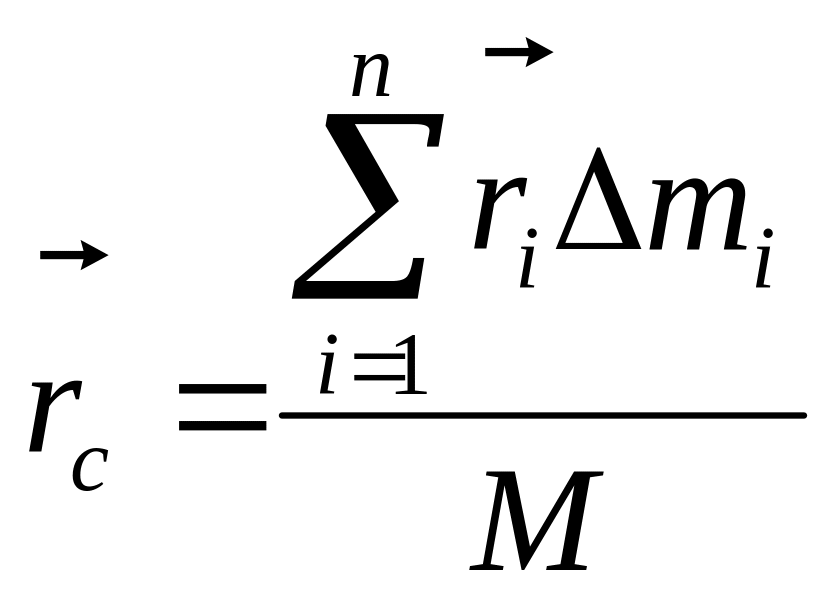(2)
И соответственно
(1’)
По формулам (2) и (2’) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор которой вычисляется по формулам (2) или (2'). В проекциях на оси координат из (2) и (2') получаем:
,
,
,
,
,
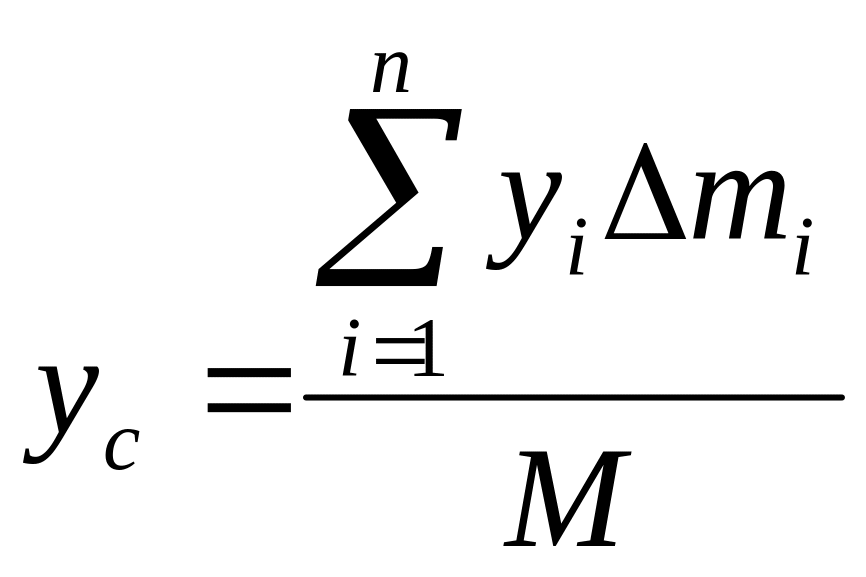где , , ‑ координаты центра масс тела.
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
,
где
-
объем элементарной частицы тела;
и
- соответственно
удельный вес
и плотность тела. Сила тяжести и масса
всего тела
,
где
-
объем
тела. Подставляя эти значения в (2) и
(2'), после сокращения на
и
соответственно
получим формулы
,
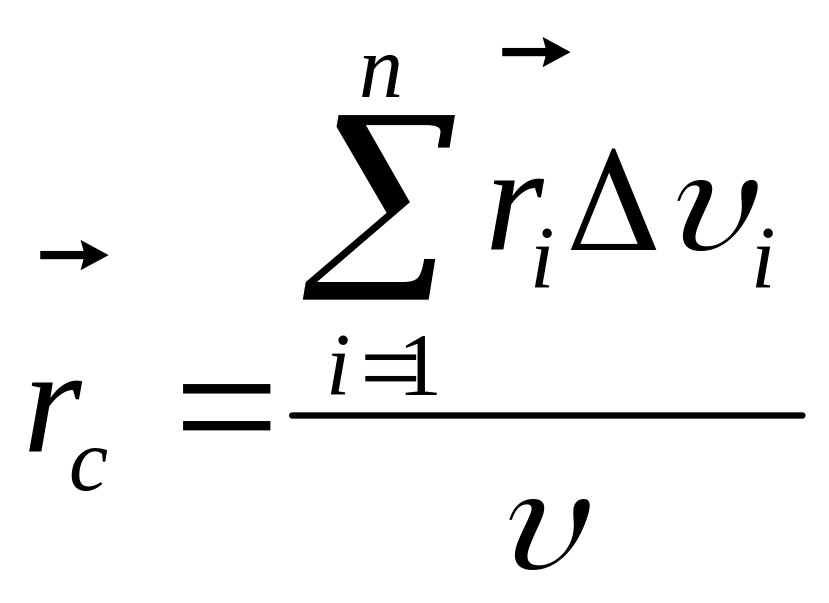по которым определяют центр тяжести объёма тела.
Если тело имеет форму поверхности, т.е. один из размеров мал по сравнению с двумя другими, как, например, у гонкого листа железа, то имеем
,
где
-
удельный вес:
- площадь элементарной частицы поверхности;
S-площадь всей поверхности.
После сокращения на
для однородной
поверхности получим следующие формулы
для определения центра тяжести ее
площади:
,
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
,
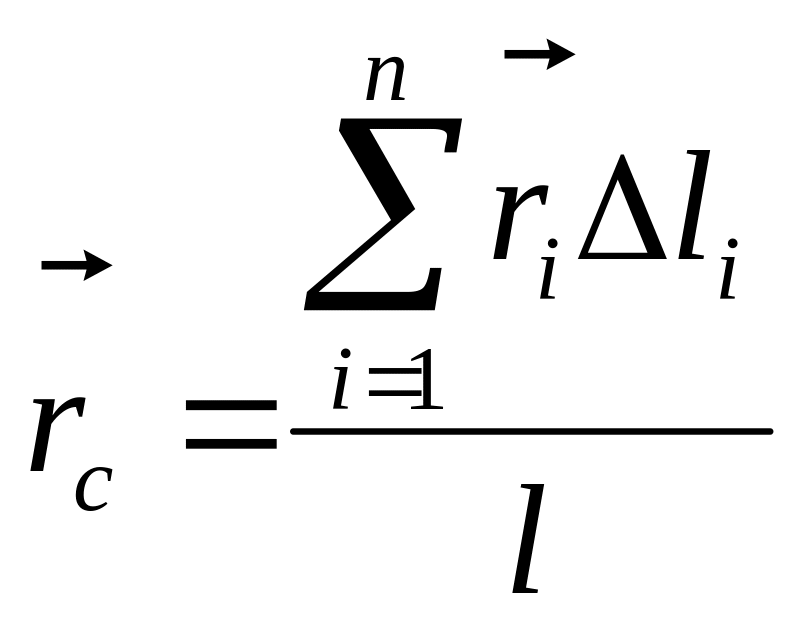где
- длина элемента линии:
- общая длина линии, центр тяжести которой
определяется.