4. Уравнение центральной винтовой оси

П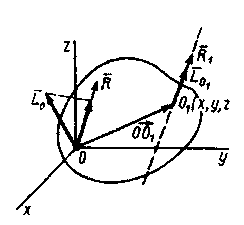 редположим, что в центре приведения, принятом за начало координат, получены главный вектор с проекциями на оси координат и главный момент с проекциями При приведении системы сил к центру приведения О₁ (рис. 30) получается динама с главным вектором и главным моментом , Векторы и как образующие линаму. параллельны и поэтому могут отличаться только скалярным множителем k_0. Имеем,, так как . Главные моменты и , удовлетворяют соотношению

Подставляя , получим

Координаты точки О₁ в которой получена динама, обозначим х, у, z. Тогда проекции вектора на оси координат равны координатам х, у, z. Учитывая это, (*) можно выразить в форме

где i. j ,k - единичные векторы осей координат, а векторное произведение * представлено определителем. Векторное уравнение (**) эквивалентно трем скалярным, которые после отбрасывания можно представить в виде

Полученные линейные уравнения для координат х, у, z являются уравнениями прямой линии - центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.

5. Частные случаи приведения пространственной

СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ

В отличие от произвольной системы сил пространственная система параллельных сил не приводится к динаме. так как для нее главный вектор и главный момент в общем случае взаимно перпендикулярны. Для доказательства )того рассмотрим пространственную систему параллельных сил для которой 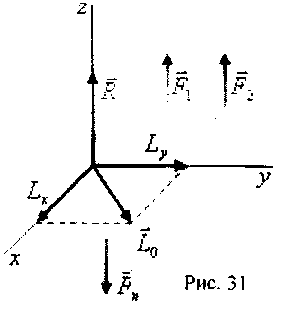главный вектор и главный момент не равны нулю. Выберем за центр приведения точку О - начало декартовой системы координат, ось Oz которой направим параллельно силам (рис.31). Тогда проекции главного вектора на оси координат

так как параллельные силы перпендикулярны этим осям. Только проекция главного вектора на ось Oz в общем случае не равна нулю. Она равна алгебраической сумме параллельных сил, т. е.

Следовательно, главный вектор параллелен оси Oz. Для проекций главного момента на оси координат имеем:

Проекция главного момента на ось Oz равна нулю, так как каждая сила параллельна этой оси.

Таким образом, главный момент расположен в плоскости Оху, перпендикулярной главному вектору, направленному по оси Oz. В этом случае система сил приводится к равнодействующей.

Для системы параллельных сил возможны следующие частные случаи приведения:

— система приводится к паре сил;

Или

— система приводится к равнодействующей силе;

— имеем равновесную систему сил.

Если главный вектор не равен нулю, то система параллельных сил приводится только к равнодействующей силе, параллельной главному вектору и равной ему по величине.

6. Центр системы параллельных сил

На твёрдое тело действует система параллельных сил . Получим формулу для определения радиус-вектора центра параллельных сил если известны параллельные силы и радиус-векторы точек их приложения. Для этого выберем единичный вектор , параллельный силам. Тогда каждая из параллельных сил

где - алгебраическое знамение силы. Оно положительно. если сила

направлена в одну сторону с единичным вектором , и отрицательно, если направление силы противоположно направлению единичного вектора. Для равнодействующей силы параллельных сил соответственно имеем

Так как система параллельных сил, по предположению, приводится к равнодействующей, то к ней можно применить теорему Вариньона относительно точки О:

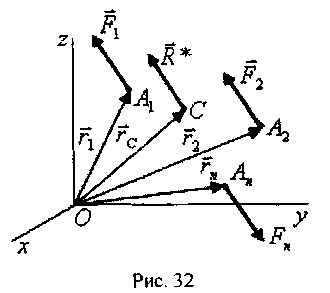
Для векторных моментов сил относительно точки О имеем

где - радиус-вектор центра параллельных сил, проведенный из точки О; -

радиус-вектор точки приложения силы F_t, проведенный из той же точки

(рис. 32).Если подставить эти значения векторных моментов сил в теорему Вариньона относительно точки О, то после переноса всех слагаемых в левую часть

равенства и вынесения за скобку общего множителя получим

Так как центр параллельных сил, а следовательно, и его радиус-вектор не зависят

от направления параллельных сил. характеризуемого единичным вектором . то вышеприведенное условие должно выполняться при любом направлении этого вектора.

Это возможно только при обращении в нуль векторной величины, стоящей в скобках, т.е.

Или

По вышеприведенной формуле определяют радиус-вектор центра параллельных сил, если заданы эти силы и их точки приложения.

Так как алгебраические значения параллельных сил входят в числитель и в знаменатель формулы, то не зависит от того, какое из двух направлений параллельных сил считается положительным.

В проекциях на оси координат из формулы получаем:

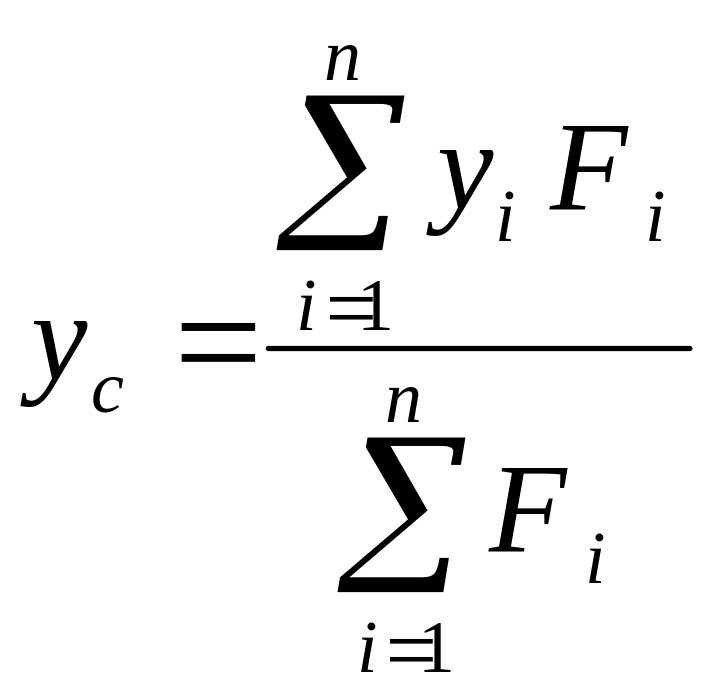
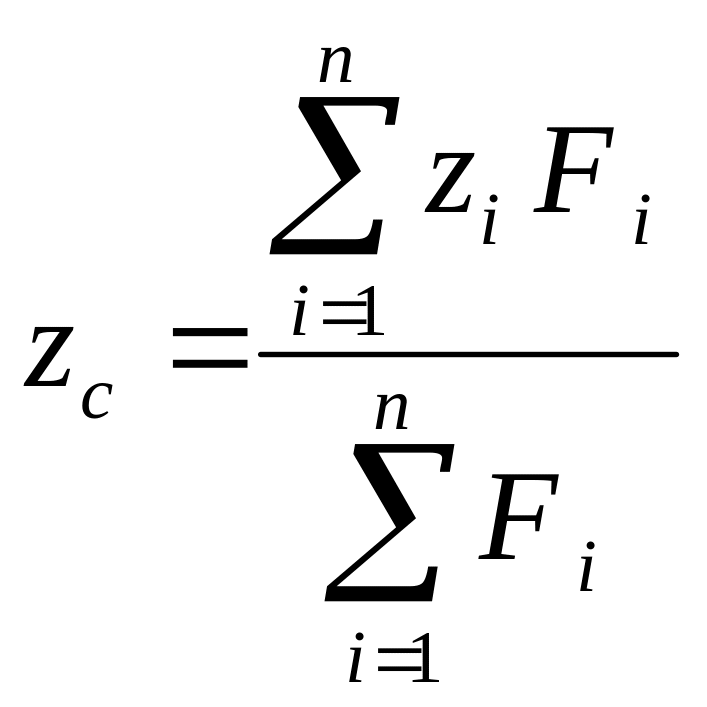
По этим формулам вычисляют координаты центра параллельных сил х_с, y_c, z_с, если известны алгебраические значения параллельных сил F_i и координаты точек приложения этих сил х_i, y_i, z_i,. Векторную величину

называют статическим моментом системы параллельных сил относительно точки О. Алгебраические величины

называют статическими моментами относительно координатных плоскостей. Для плоской системы параллельных сил, расположенных, например, в плоскости Оху, вводят понятие статических моментов относительно осей координат Ох и Оу по формулам

Статические моменты параллельных сил относительно точки и координатных плоскостей определяются по единому правилу: алгебраические значения сил умножают на расстояния от точек приложения сил до точки или плоскости и результаты суммируют.