1.3 Линейное программирование как метод решения задач математического моделирования

Задачи ЛП образуют подмножество задач математического программирования. Отличительной особенностью задач ЛП является то, что целевая функция линейная и система ограничений также линейная.

Возникновение и развитие ЛП связано с экономикой. Предположение о линейности экономических зависимостей несколько ограничивает возможности ЛП, однако простота и наглядность линейных моделей, с достаточной степенью точности описывающих экономические процессы, позволяет применять эти модели в различных видах экономической деятельности.

Большую роль в развитии ЛП сыграло создание в 1947 г. Американским ученым Дж. Данцигом универсального метода решения задач, который получил название «симплекс - метод». Была осуществлена постановка и построена модель одной из центральных задач ЛП – транспортной задачи.

Был разработан метод решения транспортной задачи (северо-западный угол, метод потенциалов).

Основная задача ЛП формулируется так:

Дана линейная целевая функция:

1)

И задана система m>n линейных неравенств (ограничений):

2) , где

3)

Найти максимум (минимум) целевой функции при выполнении условий.

1.4 Симплекс-метод как основной аппарат решения задач линейного программирования

1.4.1 Понятие о симплекс – методе

Известно, что оптимальные решения задачи ЛП связаны с угловыми точками многогранника решений. Угловых точек может быть много, если много ограничений. Количество угловых точек соответствует количеству базисных решений. Для каждого базисного решения однозначно определяется значение целевой функции. В связи с этим необходим такой переход от одного базисного решения к другому, в результате которого новое решение приносило бы в невырожденной задаче на максимум большее значение целевой функции, а в невырожденной задаче на минимум – меньшее. Данный процесс решения задачи реализует симплекс-метод, который называется методом последовательного улучшения плана. Процесс решения задачи продолжается до получения оптимального плана либо до установления факта отсутствия решений задачи.

Если задача ЛП вырожденная, то при переходе от одного базисного решения к другому значение целевой функции может не измениться. Переход от одного базисного решения к другому называется итерацией симплекс-метода или шагами.

Критерий разрешимости задачи ЛП:

Для того чтобы задача ЛП была разрешима, т.е. имела оптимальное решение, необходимо и достаточно, чтобы ограничения задачи были совместными (множество допустимых решений не пусто) и целевая функция была ограничена при поиске максимума сверху, а при поиске минимума снизу.

1.4.2 Геометрическая интерпретация симплекс – метода

Точки называются соседними, если они расположены на одном ребре. Каждое неравенство системы (1) в основной задаче ЛП определяет в евклидовом n- мерном пространстве. Полупространство, состоящее из точек x(x₁, x₂,….,x_n), расположенных по «одну сторону» от плоскости и на самой этой плоскости. Система неравенств , где (1) образует некоторый выпуклый многогранник Ω.

Значение целевой функции (2) в точке x^΄(x₁^΄,...,x_n^΄) можно рассматривать как уклонение этой точки от плоскости (3).

Понимая под уклонением данной точки от этой плоскости число, которое получим, подставив в левую часть уравнения (2) координаты этой точки x^΄. Уклонение точки x от плоскости (3) пропорционально расстоянию от точки до этой плоскости.

Таким образом, геометрический смысл задачи ЛП заключается в отыскании в многограннике Ω точки, которая наиболее (наименее) уклонена от плоскости (3).

1.4.3 Алгоритм симплекс – метода

Основу алгоритма симплекс-метода составляет последовательность шагов, реализующая переход от одного базисного плана к другому и приводящая либо к оптимальному решению, либо к выводу о том, что задача ЛП решения не имеет.

Симплекс-метод состоит из алгоритма отыскания опорного решения системы линейных неравенств и из алгоритма последовательного перехода от полученного уже опорного решения системы (1) к оптимальному решению.

Для лучшего понимания алгоритма симплекс-метода необходимо описать каждый его шаг.

1. В начале задача записывается в симплекс-таблицу. Затем просматриваются свободные члены в строке относительных оценок. Если они имеют отрицательные значения, это свидетельствует, что решение не является оптимальным и его можно улучшить. Улучшение достигается построением новой симплекс-таблицы до тех пор, пока в строке относительных оценок не будут стоять положительные значения.

2. В исходной таблице выбирается ключевой столбец – это тот столбец, которому соответствует минимальный, отрицательный элемент в

строке относительных оценок. Если их несколько, то выбирается любой из них.

3. В исходной таблице выбирается ключевая строка. Для ее выбора необходимо каждый элемент в столбце результата разделить на соответствующий ему положительный элемент ключевого столбца. Минимальное частное из полученных чисел соответствует ключевой строке.

4. Выбирается ключевой элемент. Этим элементом является число, стоящее на пересечении ключевого столбца и ключевой строки.

5. Строится макет новой симплекс-таблицы, в которой меняются местами базисная и небазисная переменные, соответствующие ключевому столбцу и ключевой строке.

6. Ключевой элемент заменяется обратным к нему по отношению к операции деления.

7. В ключевом столбце все элементы делятся на ключевой элемент, и знак меняется на противоположный. В ключевой строке все элементы делятся на ключевой элемент, и знак не меняется.

8. Все остальные элементы находятся по правилу:

1.4.4 Симплексные таблицы

Симплексные таблицы необходимы для пересчета данных. Они представляют собой прямоугольники. Наверху таблицы записываются основные переменные со знаком минус (для модифицированных жордановых исключений). Слева таблицы – дополнительные переменные, которые неравенства преобразуют в равенства. Справа- столбец свободных членов системы. Внизу - строка коэффициентов целевой функции.

Таблица 1

	-х1	-х2	…	-хn	1
У1	А11	А12	…	А1n	В1
Уi	…	…		…	…
Уm	Аm1	Аm2	…	Аmn	Вm
F	С1	С2	…	Сn	0

1.4.5 Особые случаи симплекс-метода

1. Отсутствие конечного оптимума возникает, когда все элементы разрешающего столбца отрицательные и нельзя составить отношение положительных свободных членов к этим элементам. В этом случае область допустимых решений не ограничена и целевая функция равна бесконечности.

2. Появление вырожденного базисного решения. Когда минимальное отношение свободного члена к элементу разрешающего столбца равно нулю. Выход из вырождения осуществляется при выборе минимального отношения чуть больше нуля.

Оптимальное решение может быть не единственным, а множество решений, которое можно представить как выпуклую линейную комбинацию базисных решений. Геометрически это означает, что целевая функция параллельна ребру многогранника Ω.

2 Практическая часть

2.1 Постановка задачи с экономическим обоснованием

Предприятие изготавливает три вида продукции из трех видов ресурсов.

Продукции содержат определенное количество ресурсов А=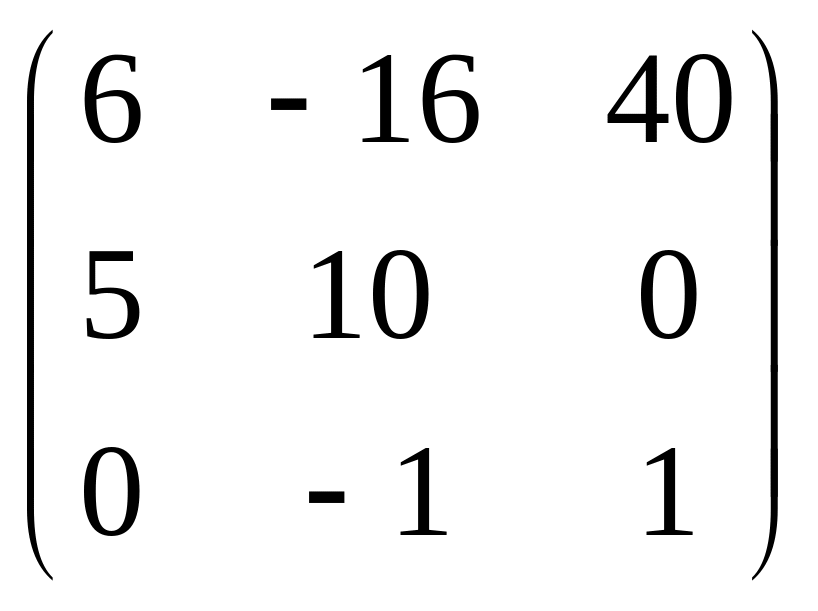 . Запас ресурсов трех сортов известен: 45; 25; 16. Прибыль производство одной единицы каждой продукции соответственно равна С=(6, 10, 1).

Требуется составить такой план производства продукции, при котором прибыль производство всего произведенного объема была максимальна.

2.2 Запись задачи в виде математической модели линейного программирования

Составим математическую модель для описания данной задачи и убедимся, что данная задача относится к задаче линейного программирования.

Пусть x₁, x₂, x₃ количество продукции 1-го, 2-го, 3-го видов соответственно, которые нужно произвести, чтобы получить максимальную прибыль, тогда целевая функция, то есть функция прибыли будет иметь вид:

F=6x₁+10x₂+x₃max

Составим систему ограничений:

Ограничения для продукции 1-го вида 6x₁-16x₂+40x₃≤45

Ограничения для продукции 2-го вида 5x₁-10x₂≤25

Ограничения для продукции 3-го вида -x₂+x₃≤16

Так как мы производим продукцию, то переменные x₁, x₂, и x₃ подчиняются следующему требованию x₁≥0,x₂≥0 и x₃≥0.

Таким образом, математическая модель к данной задаче имеет вид:

F=6x₁+10x₂+x₃max

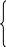6x₁-16x₂+40x₃≤45

5x₁-10x₂≤25

-x₂+x₃≤16

x₁≥0,x₂≥0, x₃≥0.

2.3 Геометрический метод решения задачи ЛП

Предлагается реализовать графический метод для двух неизвестных. Следовательно, исходные данные будут иметь вид:

F=6x₁+10x₂max

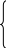6x₁-16x₂≤45

5x₁-10x₂≤25

-x₂≤16

x₁≥0,x₂≥0.

Построим область допустимых решений функции F:

Для этого в ограничениях знаки неравенства заменяем знаками равенства. Из полученных уравнений находим координаты точек и строем полученные прямые. Затем определяем полуплоскости, соответствующие данным ограничениям, и получаем область допустимых решений, лежащую на пересечении всех полуплоскостей.

Построим прямую уровня. Возьмем произвольную точку М из области допустимых решений и, подставив её координаты в функцию F, получим координаты точек прямой уровня. Затем от М проводим вектор А, координаты которого – это коэффициенты целевой функции F.

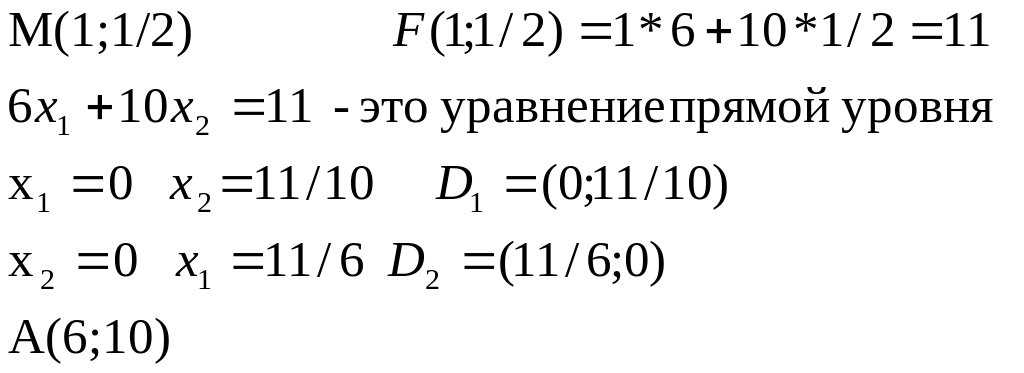
Максимизируем (минимизируем) функцию. Для этого передвигаем прямую уровня по направлению (в обратном направлении) относительно вектора А до пересечения с граничной точкой области допустимых решений, полученная точка является оптимальным решением.

Подставив координаты этой точки , в функцию F, получим max или min.

Оптимальная точка имеет координаты (5,0).

Ответ: Предприятие достигает максимального дохода Fmax=30 при оптимальном плане, где x₁=5 1-го вида, x₂=0 2-го вида, т.е. при производстве продукции этого вида, предприятие достигает максимального дохода.

График функции с ограниченной областью допустимых значений будет иметь следующий вид (рисунок 1).

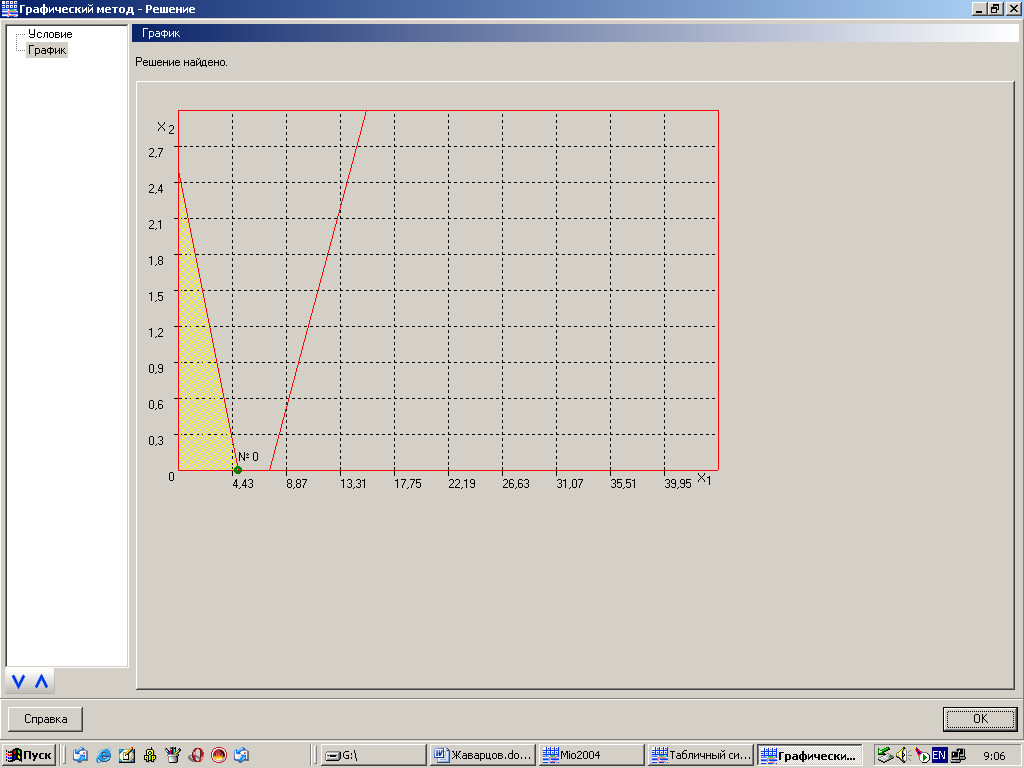
Рисунок 1 – График

2.4 Симплексный метод решения задачи ЛП

F=6x₁+10x₂+x₃max

6x₁-16x₂+40x₃≤45

5x₁-10x₂≤25

-x₂+x₃≤16

X₁≥0,x₂≥0,x₃≥0.

Для использования симплекс метода необходимо привести задачу к каноническому виду.

Запись задачи в каноническом виде:

F=6x₁+10x₂+x₃max

6 x₁-16x₂+40x₃+x₄=45

5x₁-10x₂+x₅=25

-x₂+x₃+x₆=16

x_i≥0, i=1..6

Построение начальной симплекс – таблицы:

	X1	X2	X3
X4	6	-16	40		45
X5	5	10	0		25
X6	0	1	1		16
	-6	-10	-1		0

Выбираем ключевой столбец – это второй столбец, так как ему соответствует минимальный, отрицательный элемент в строке относительных оценок =-10. Определяем ключевую строку. Для этого делим каждый элемент в столбце результата на соответствующий ему положительный элемент в ключевом столбце. Следовательно, ключевой строкой будет являться вторая строка. Ключевой элемент = 10.

Построение второй симплекс – таблицы.

Строим макет второй симплекс таблицы и меняем местами x2 и x5. Заменяем ключевой элемент на обратный к нему, относительно операции деления, т.е. на 1/10. Делим ключевой столбец на ключевой элемент и меняем знак. Ключевую строку делим на ключевой элемент, знак при этом не меняем. Остальные элементы находим по определенному правилу:

Вторая симплекс – таблица:

	X1	X5	X3
X4	14	8/5	40		85
X2	½	1/10	1		5/2
X6	½	1/10	0		37/2
	-1	1	-1		25

Третья симплекс – таблица:

	X2	X5	X3
X4	-28	-6/5	40		15
X1	2	1/5	0		5
X6	-1	0	1		16
	2	6/5	-1		30

Четвертая симплекс – таблица:

	X2	X5	X4
X3	-7/10	-3/100	1/40		3/8
X1	2	1/5	0		5
X6	-3/10	3/100	-1/40		128/5
	13/10	117/100	1/40		243/8

Построенная таблица является оптимальной, так как в строке относительных оценок все элементы положительны. Для записи ответов используем следующее правило. Если переменные x₁, x₂ ,x₃ являются в оптимальной таблице базисными, то их значения выписываются из столбца результата. Если какая-нибудь из переменных x₁ или x₂, или x₃ является в оптимальной таблице небазисной, то ее значение равно 0. Таким образом, для нашей задачи значение x₁=5, x₂=0, x₃=3/8, а F=6*5+10*0+1*3/8=243/8.

2.5 Экономическая интерпретация двойственной задачи. Оценка дефицитных и недефицитных ресурсов

Построение двойственной задачи

Исходная задача:

F=6x₁+10x₂+x₃max

6x₁-16x₂+40x₃≤45

5x₁-10x₂≤25

-x₂+x₃≤16

x₁≥0,x₂≥0,x₃≥0

Двойственная задача:

G=45y₁+25y₂+16y₃min

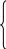6y₁+5y₂-y₃≥6

-16y₁-10y₂-1y₃≥10

40y₁+y₃≥1

y₁≥0,y₂≥0,y₃≥0

Основная теорема двойственности (1-ая теорема):

Если одна из двойственных задач обладает оптимальным решением, то и другая имеет оптимальное решение, причем оптимальные значения целевых функций равны:

1. Fmax=fmin=Q

Условия дополняющей нежесткости (2-ая теорема):

Для того чтобы два допустимых решения X(x₁,…x_n) и Y(y₁,…y_m) двойственных задач были оптимальными, необходимо и достаточно, чтобы эти решения удовлетворяли так называемым “условиям дополнительной нежесткости”:

2)

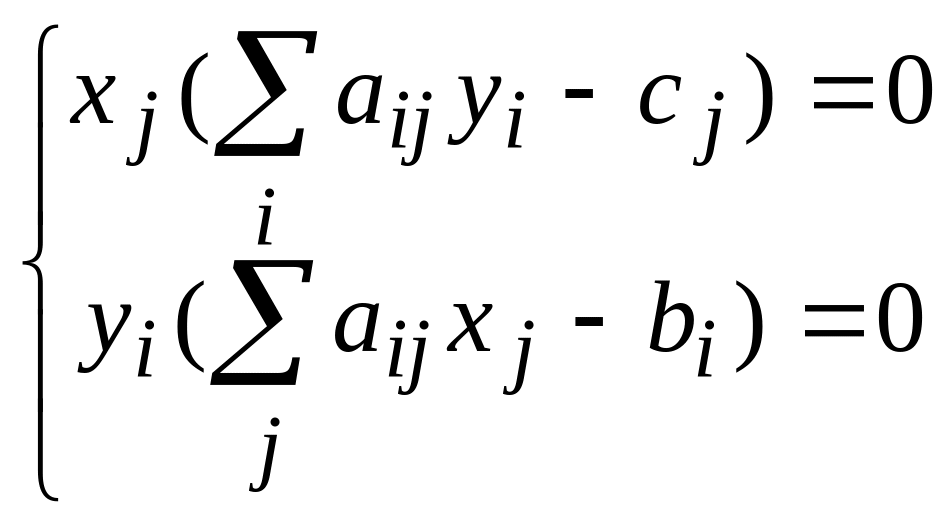
Если какая – нибудь переменная отлична от нуля, то выражение в скобках (2) обращает в нуль строгое равенство и наоборот.

На основе двух теорем двойственности выполняется заключение: можно решать любую из задач, а ответ получить для двух задач, т.к. задачи №1 и №2 взаимно-двойственные.

Решим двойственную задачу симплекс-методом:

1-я исходная симплекс-таблица:

	Y4 X1	Y5 X2	Y6 X3
Y1 X4	6	-16	40		45
Y2 X5	5	10	0		25
Y3 X6	0	1	1		16
	-6	-10	-1		0

2-я конечная симплекс-таблица:

	Y5 X2	Y2 X5	Y1 X4
Y6 X3	-7/10	-3/100	1/40		3/8
Y4 X1	2	1/5	0		5
Y3 X6	-3/10	3/100	-1/40		128/5
	13/10	117/100	1/40		243/8

Решив двойственные задачи № 1 и №2 симплекс – методом, получим следующие оптимальные решения:

И оптимальные значения целевых функций Fmax=fmin=243/8

Решение двойственных задач имеет экономический смысл.

Из условия: Fmax=fmin=243/8 вытекает, что предприятию безразлично, производить ли продукцию по оптимальному плану и получать максимальную прибыль (выручку) Fmax=243/8, либо продавать ресурсы по оптимальным ценам и возместить от продажи равные ей минимальные затраты на ресурсы fmin=243/8.

Обоснование оптимальных планов и :

означает количество производимой предприятием продукции.

объективно обусловленные оценки ресурсов.

виды продукции рентабельные; означает, что ресурсы используются полностью в оптимальном плане .

По оптимальному плану производства дефицитные ресурсы (т.е. полностью используемые) получат ненулевые оценки , а недефицитные нулевые оценки .

В задачах №1 и №2 получены объективно обусловленные оценки ресурсов , т.е. при увеличении (уменьшении) запаса ресурсов b1=45, b2=25 прибыль увеличится (уменьшится) соответственно на 1/40 и 1.17 руб.