6.5. Визначення обсягу вибірки і способи поширення вибіркових даних

Проектуючи вибіркові обстеження, визначають мінімально достатній обсяг вибірки, за якою вибіркові оцінки репрезентували б основні властивості генеральної сукупності.

Чисельність вибірки залежить від таких факторів:

а) варіації досліджуваної ознаки. Чим більша варіація, тим більшою має бути чисельність вибірки, і навпаки;

b) розміру можливої граничної похибки вибірки. Чим менший розмір можливої похибки, тим більшою має бути чисельність вибірки;

с) значення ймовірності, з якою гарантуватимуть результати вибірки. Чим більша ймовірність, тим більшою має бути чисельність вибірки;

d) способу добору одиниць у вибіркову сукупність.

Для власне випадкової та механічної вибірки при повторному відборі

;

при без повторному −

.

Для визначення обсягу вибірки n використовують оцінки дисперсій аналогічних пробних обстежень; якщо такі обстеження відсутні, можна скористатися співвідношенням: , а для частки взяти значення дисперсії .

6.6. Способи поширення вибіркових даних на генеральну сукупність

Кінцевою метою будь-якого вибіркового спостереження є поширення його характеристик на генеральну сукупність. Розрізняють два способи поширення даних вибіркового спостереження: прямий перерахунок та метод коефіцієнтів.

1. Прямий перерахунок використовують у тому випадку, коли треба визначити обсяг ознаки у генеральній сукупності. Робиться це так: середній розмір ознаки, обчислений в результаті вибіркового спостереження, треба помножити на чисельність одиниць генеральної сукупності.

2. Якщо вибіркове спостереження проводять з метою уточнення результатів суцільного спостереження, застосовують метод коефіцієнтів.

Припустимо, що суцільний перепис показав, що об’єм ознаки m. Під час контрольної перевірки 10% елементів сукупності було встановлено, якщо при суцільному спостереженні обсяг ознаки становив m, то при контрольному – . Таким чином не враховано ознаки, якщо , або враховано лишніх ознаки, якщо . Числа або є поправочними коефіцієнтами.

Відбір вважається задовільним, якщо . Якщо , вибірка вважається не репрезентативною і відбір повторюється або ж збільшується чисельність вибірки.

6.7. Статистична перевірка гіпотез

Статистична гіпотеза — це певне припущення щодо властивостей генеральної сукупності, яке можна перевірити спираю­чись на результати вибіркового спостереження. Суть перевірки гіпотез полягає в тому, щоб визначити, узгоджуються чи ні результати вибірки з гіпотезою, випадковими чи невипадковими є розбіжності між гіпотезою і даними вибірки. Найчастіше гіпотеза, яку належить перевірити, формулюється як відсутність розбіжності (нульова розбіжність) між невідомим параметром генеральної сукупності G і заданою величиною А, а тому її позначають H₀. Зміст гіпотези записують після двокрапки, наприклад Н₀: G = А.

Кожній нульовій гіпотезі протиставляють альтернативну Н_а. При формулюванні Н_а враховується вагомість відхилень (G - А): для додатних відхилень Н_а: G > А, для від’ємних — Н_а: G < А, для тих і інших - Н_а: G ≠ А.

Якщо вибіркові дані суперечать гіпотезі H₀, вона відхиляється, коли ці дані узгоджуються з гіпотезою H₀, вона не відхиляється. Спираючись на результати вибірки, статистична перевірка гіпотез неминуче пов’язана з ризиком прийняття помилкового рі­шення: ризик І — відхилення правильної нульової гіпотези, ризик II — невідхилення нульової гіпотези, коли насправді пра­вильною є альтернативна. Ці ризики конкуруючі, і зменшення імовірності α одного зумовлює збільшення ймовірності β іншо­го. Оскільки уникнути ризиків неможливо, а наслідки їх, як правило, різновагомі, то в кожному конкретному дослідженні праг­нуть мінімізувати той ризик, який пов’язаний з більшими втратами. Ймовірності ризиків наведено в табл.6.7.1.

Таблиця 6.7.1.

Правильна гіпотеза	Прийнята гіпотеза
	H0	Hа
H0	1-α	α
Hа	Β	1-β

Правило, за яким гіпотеза H₀ відхиляється або не відхиляється (приймається), називається статистичним критерієм. Матема­тичною основою будь-якого критерію є статистична характерис­тика Z, значення якої визначається за даними вибірки, а закон розподілу відомий. Кожне значення характеристики Z має певну ймовірність Р (Z). Якщо вибіркове значення Z малоймовірне, гі­потеза H₀ відхиляється.

Межу малоймовірності Z називають рівнем істотності α. Очевидно, що α — це ймовірність ризику І, а тому залежно від змісту гіпотези H₀ і наслідків її відхилення рівень істотності ви­значають у кожному конкретному дослідженні. Зазвичай виби­рають один із рівнів α, для яких табульовані значення статистич­них характеристик критеріїв. Це α = 0,10; 0,05; 0,025; 0,01.

Значення статистичної характеристики критерію Z_1-α поділяє множину вибіркових значень Z на дві частини: а) область допус­тимих значень і б) критичну область. Якщо вибіркове значення Z потрапляє у критичну область, гіпотеза H₀ відхиляється, якщо в область допустимих значень — не відхиляється. Саме тому зна­чення Z_1-α називають критичним.

Залежно від того, як сформульована альтернативна гіпотеза, критична область може бути односторонньою (ліво- чи правосторонньою) або двосторонньою (рис. 6.7.1).

α

Z

α /2

α /2

Z

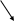
Рис. 6.7.1. Лівостороння та двосторонньою критичні області

Статистична гіпотеза перевіряється в такій послідовності:

а) формулюють нульову H₀ та альтернативну Н_а гіпотези;

б) вибирають статистичну характеристику Z, за значеннями якої перевіряють правильність гіпотези H₀ ;

в) визначають рівень істотності α і відповідне йому критичне значення Z_1-α; залежно від формулювання гіпотез H₀ і Н_а критична область може бути одно- або двосторонньою;

г) за результатами вибірки розраховують фактичне (вибірко­ве) значення статистичної характеристики Z, яке порівнюють з критичним Z_1-α ; якщо Z> Z_1-α , гіпотеза H₀ відхиляється, при Z < Z_1-α - не відхиляється.