4.6. Обчислення середньої арифметичної інтервального ряду розподілу

1. Якщо варіаційний інтервальний ряд розподілу має відкриті інтервали, то, перш за все, їх треба закрити за розмірами інтервалів, розташованих поруч.

2. Знаходимо середину інтервалів: до нижньої границі інтервалу додаємо верхню і ділимо на 2.

3. Знаходимо середню, використовуючи замість середньої величини по кожній групі середину інтервалу.

Середня для інтервальних варіаційних рядів – величина приблизна. Це пояснюється тим, що середина інтервалу відрізняється від середнього значення, якщо варіанти в межах інтервалу розташовані нерівномірно.

5. Показники варіації

5.1.Необхідність вивчення варіації

Характеристика сукупності буде недостатньою, якщо обмежитись лише середніми величинами. Середні величини не показують, як розміщені навколо них окремі варіанти ознаки, яка вивчається. За характером та мірою відхилення можна зробити висновок щодо якісної однорідності статистичної сукупності та надійності самої середньої величини.

Вивчення варіації ознаки дає можливість визначити, які фактори і якою мірою впливають на виконання договірних зобов’язань окремих підприємств, на врожайність пшениці, продуктивність праці робітників і т.п. Вивчення варіації ознаки потрібне для наукової організації вибіркового спостереження, кореляційного та дисперсійного аналізу.

5.2. Показники варіації

1. Розмах варіації – це різниця між найбільшим і найменшим значенням ознаки:

Він характеризує межі, в яких варіюють значення ознаки. Використовують для попередньої оцінки варіації.

2. Середнє лінійне відхилення – середнє значення з модулів відхилень кожного варіанту від середнього значення.

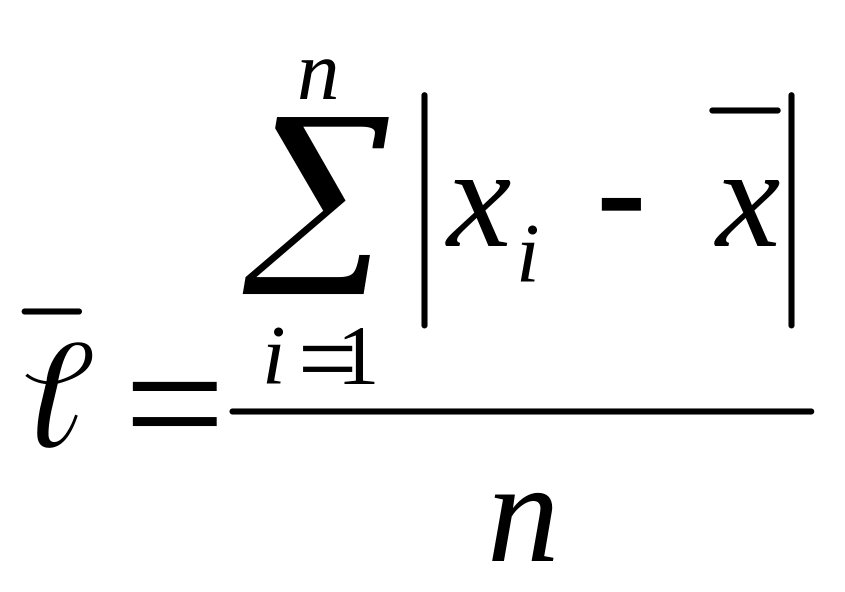або

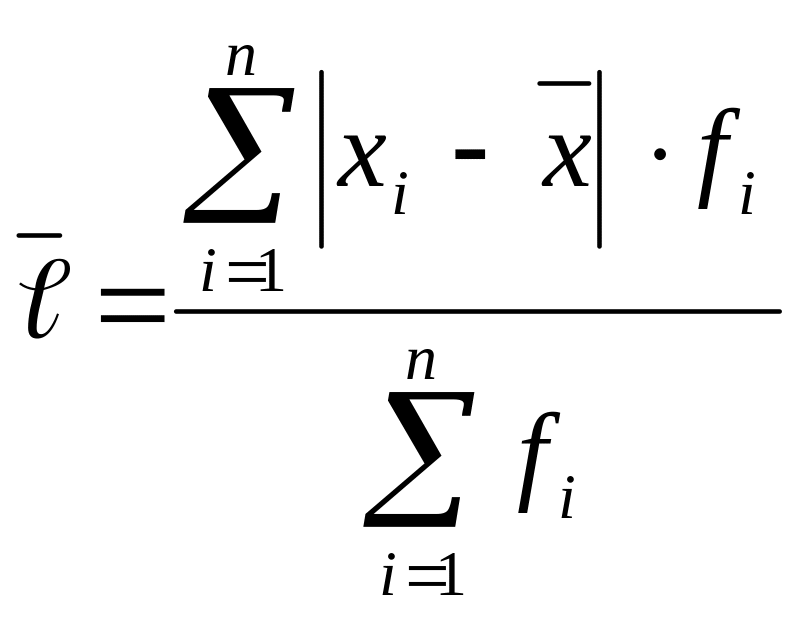
3. Ще один спосіб усереднення відхилень варіант від середньої арифметичної, що дозволяє обійти складність, зумовлену рівністю нулю їх алгебраїчної суми – розрахунок квадратів відхилень варіант від середньої з наступним їх усередненням. Цей показник називається дисперсією.

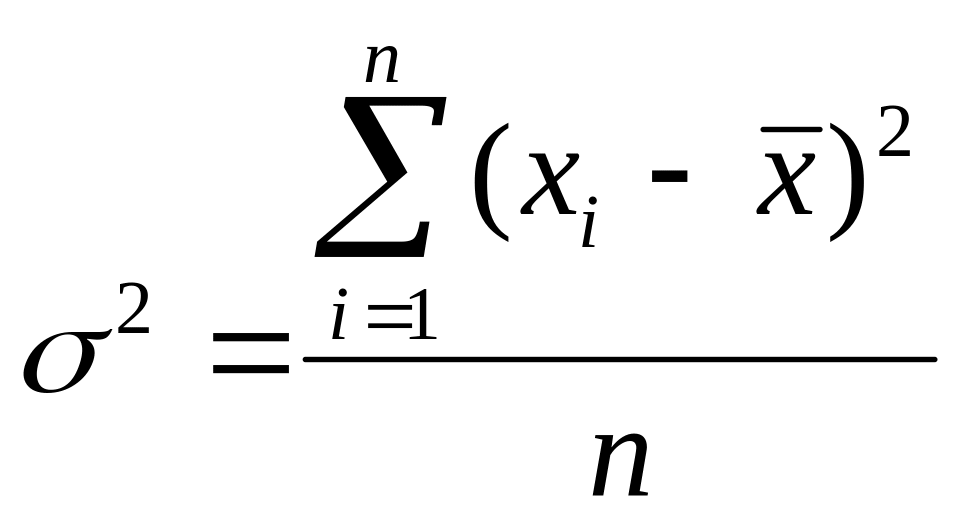або

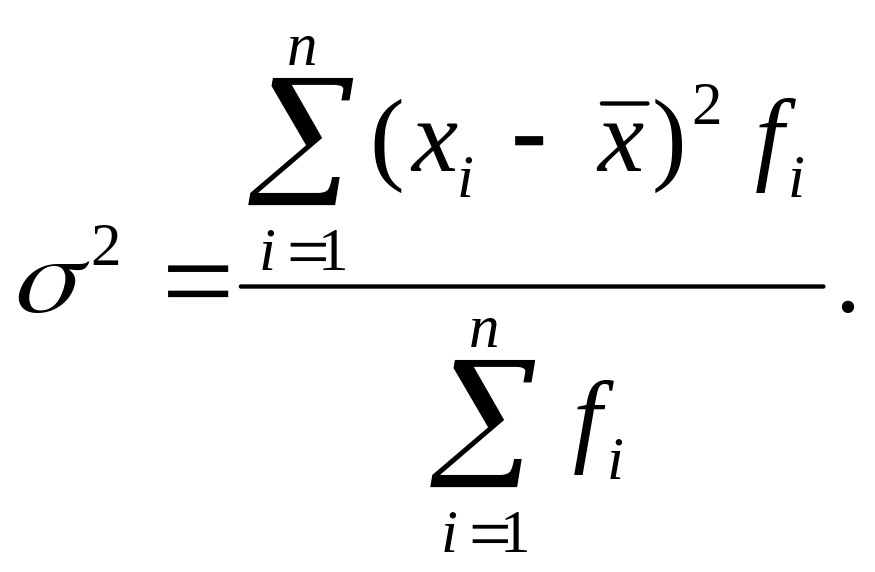
4. Середнє квадратичне відхилення – характеризує абсолютне коливання значень варіюючої ознаки і виражається в тих самих одиницях, що і варіанти.

5. В статистичній практиці часто виникає необхідність порівняння варіації різних ознак. Для цього вищезгадані показники не можна використовувати.

Для здійснення такого роду порівнянь статистика використовує коефіцієнт варіації – виражене в процентах відношення середнього квадратичного відхилення до середньої арифметичної

5.3. Характеристики форми розподілу

Аналіз закономірностей розподілу передбачає оцінювання ступеня однорідності сукупності, асиметрії та ексцесу розподілу.

Однорідність сукупності – передумова використання інших статистичних методів. Однорідними вважаються такі сукупності, елементи яких мають спільні властивості і належать до одного типу, класу. При цьому однорідність не означає повну тотожність властивостей елементів, а лише наявність у них спільного в істотному.

В однорідних сукупностях розподіли одновершинні. Багатовершинність свідчить про однорідний склад сукупності. Критерієм однорідності сукупності вважається квадратичний коефіцієнт варіації, який завдяки властивостям середньоквадратичного відхилення в симетричному розподілі становить .

З-поміж одновершинних розподілів є симетричні та асиметричні (скошені), гостро- та плосковершинні. У симетричному розподілі віддалені від центра значення ознаки мають однакові частоти. А в асиметричному – вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена вліво, маємо правосторонню асиметрію, і навпаки. Асиметрія виникає внаслідок обмеженої варіації в одному напрямку або під впливом домінуючої причини розвитку, яка призводить до зміщення центра розподілу.

В симетричному розподілі , при правосторонній асиметрії – , при лівосторонній – . Чим більша асиметрія, тим більшим є відхилення .

Найпростішою мірою асиметрії є відхилення , яке характеризує напрям і міру скошення в середині розподілу. При правосторонній асиметрії – А>0, при лівосторонній – А < 0.

Теоретично коефіцієнт асиметрії не має меж, проте на практиці його значення не буває надто великим і в помірно скісних розподілах не перевищує одиниці.

Ексцес – це властивість одновершинних розподілів, яка характеризує ступінь зосередженості елементів сукупності навколо центра розподілу.

Асиметрія і ексцес – дві пов’язані з варіацією властивості форми розподілу. Комплекс їх оцінювання виконується на базі центральних моментів розподілу – середньої арифметичної k-того ступеня відхилення індивідуальних значень ознаки від середньої:

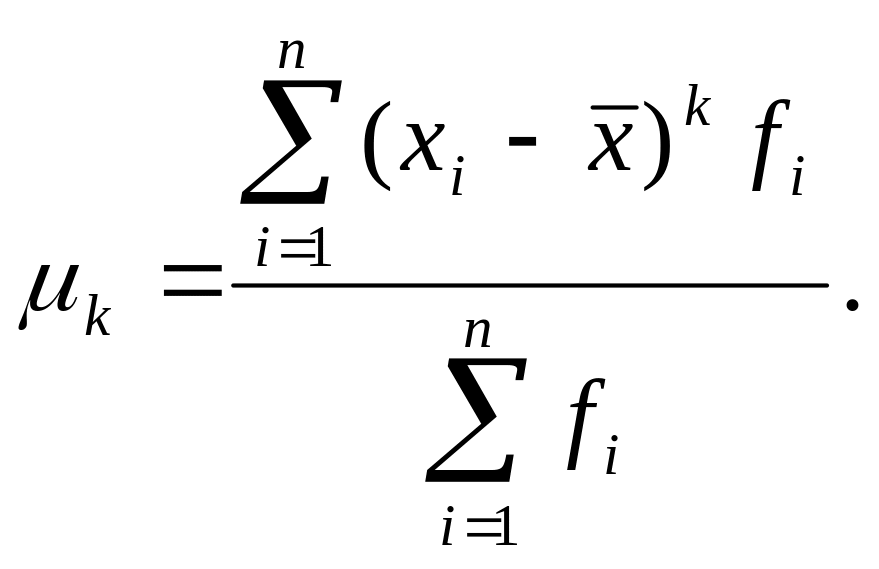
Момент другого порядку – це дисперсія, третього – асиметрія, четвертого – ексцес. Для того, щоб характеристика скошеності не залежала від масштабу вимірювання ознаки, для порівняння ступеня асиметрії різних розподілів використовується стандартизований момент, який залежить від крайніх значень ознаки на відміну від коефіцієнта скошеності: При правосторонній асиметрії – А_S >0, при лівосторонній – А_S < 0.

При А_S < 0,25 асиметрія низька, при А_S < 0,5 – середня, при А_S >0,5 – висока.

Стандартизований коефіцієнт ексцесу: В розподілі, близькому до нормального Е_K = 3, при гостровершинному – Е_K > 3, при плосоквершинному −Е_K < 3.

Не менш важливими в статистичному аналізі є характеристика нерівномірності розподілу ознаки між окремими складовими сукупності та оцінка концентрації значень ознаки в окремих її частинах.

Оцінка концентрації ґрунтується на відхиленнях часток двох розподілів – за кількістю елементів сукупності та обсягом значень ознаки .

Якщо розподіл значень ознаки в сукупності рівномірний. То частки однакові - = , відхилення часток свідчать про певну концентрацію. Коефіцієнт концентрації:

К=0 – рівномірний розподіл, К=1 повна концентрація, чим більше значення коефіцієнта концентрації, тим вищим є ступінь концентрації.

Коефіцієнт концентрації широко використовується при регіональному аналізі для оцінювання рівномірності територіального розподілу виробничих потужностей, фінансових ресурсів тощо. За кожним регіоном визначається також коефіцієнт локалізації:

який характеризує співвідношення часток.

Наступною характеристикою розподілу є коефіцієнт подібності структур:

Якщо Р=1, то структури однакові, якщо Р=0 – абсолютно протилежні, чим більше схожі структури, тим більшим є значення Р.

Структура будь-якої сукупності динамічна. Зміна часток окремих складових сукупності свідчить про структурні зрушення, інтенсивність яких оцінюється за допомогою середнього лінійного або середнього квадратичного відхилення часток:

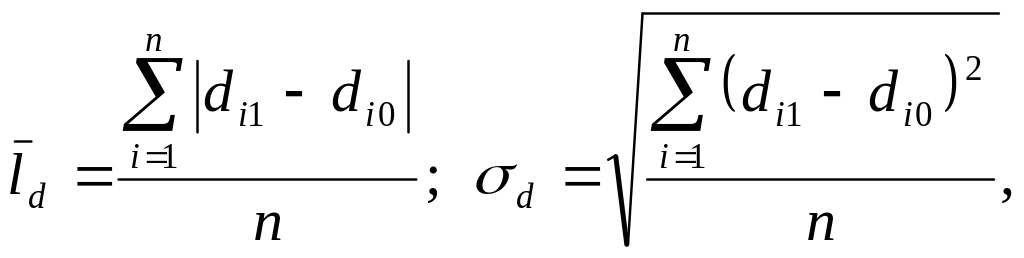
де d_i0 та d_i1 – частки відповідно базисного та поточного періодів, n – число складових сукупності.