Виды средних: общие, групповые, среднее арифметическое, среднее геометрическое, среднее гармоническое. Структурные средние: мода, медиана.
Средней величиной в статистике называют обобщающий показатель, характеризующий общественное явление по одному количественному признаку (или типический размер признака данной совокупности).
Статистические средние – это реальные показатели, отражающие объективно существующие свойства общественных явлений (производительность труда, стоимость товара, урожайность, национальный доход на душу населения). Явления существуют в жизни, а статистикой характеризуются в виде определенных показателей.
Виды средних
В статистике различают прямые и обратные величины, первичные и вторичные. Так как статистическая размерность различна, то приходится применять в расчетах различные виды средних: арифметическую, гармоническую, геометрическую.
Для первичных признаков применяются простые средние, для вторичных – взвешенные. Наиболее распространенной является средняя арифметическая простая, которая применяется в расчетах, когда единицы изучаемой совокупности представлены индивидуальными значениями признака (m = 1).
Средняя арифметическая взвешенная применяется в расчетах, когда индивидуальные значения определяемого признака имеют различную частоту повторения.
Свойства средней арифметической
Метод исчисления средней арифметической обладает рядом математических свойств, которые используются в статистике для упрощения техники расчетов. Важнейшие из этих свойств следующие.
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты средней:
2. Сумма отклонений индивидуальных значений признака от средней арифметической равна 0.
3. Если все осредняемые варианты увеличить или уменьшить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину.
4. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:
5. Если частоты уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:
Объединяя свойства средней арифметической, можно исчислить ее с помощью способа моментов.
Средняя гармоническая применяется, когда индивидуальные значения выражены в форме обратных показателей. Если вес каждого варианта равен единице, то при n вариантах формула средней гармонической имеет вид
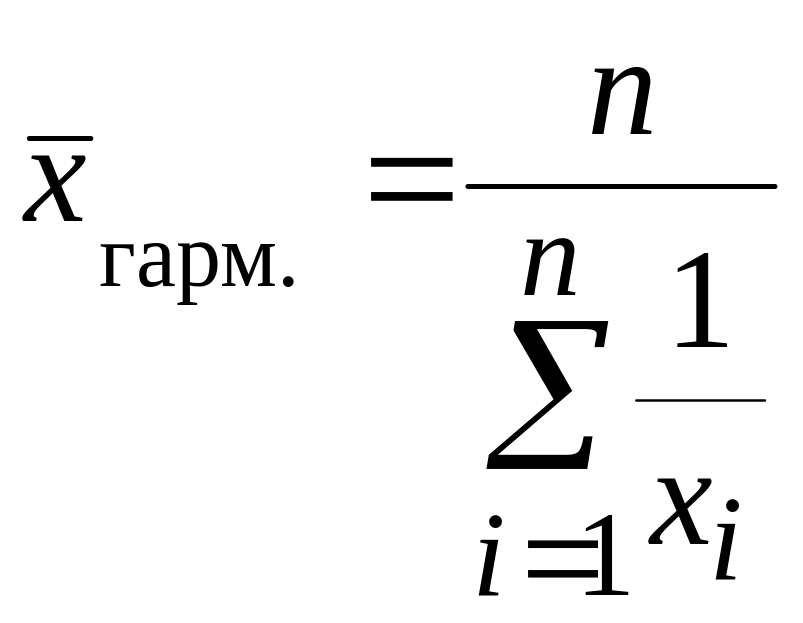. (4.11)
Средняя геометрическая применяется для расчетов средних темпов за определенный период, т. е. тогда, когда определяющий показатель (величина, определяющая вид средней) является не суммой значений, а их произведением:
(простая); (4.13)
Структурные средние
Модой в статистике называется величина признака (варианта), которая наиболее часто встречается в данной совокупности.
В интервальном ряду моду определяют по формуле:
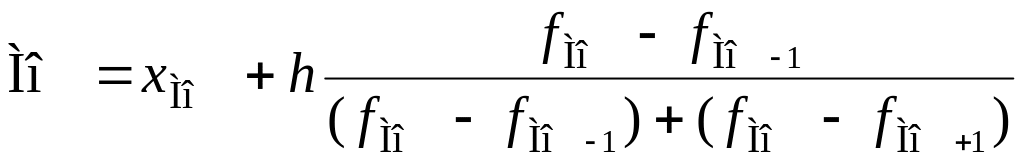(4.17)
где 
– нижняя граница модального интервала;
– частота модального интервала;
– частота предмодального интервала;
– частота интервала, следующего за
модальным;
– величина интервала.
Медианой в статистике называется значение признака у единицы, которая расположена в середине упорядоченного ряда, а в вариационном ряду медианой будет величина признака, которая делит ряд пополам по сумме накопленных частот.
По данным интервального вариационного ряда медиана определяется по следующей формуле:
,
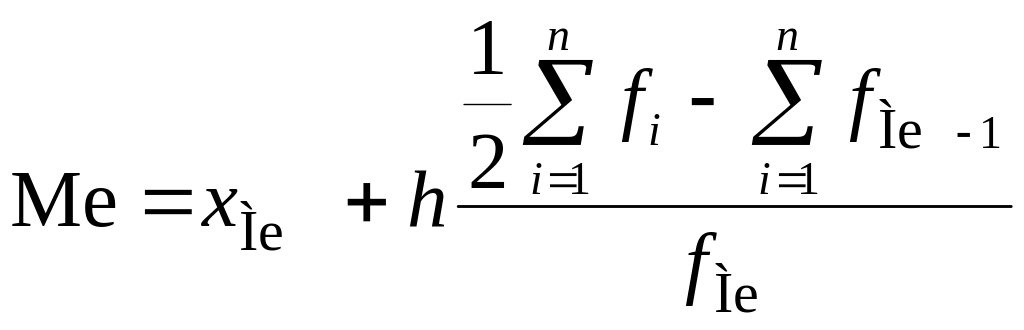(4.18)
где 
– медиана;
–
нижняя граница медианного интервала;
– сумма накопленных частот;
– сумма накопленных частот, предшествующих
медианному интервалу;
– частота медианного интервала;
h – величина медианного интервала.
Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Выбирается самый высокий прямоугольник, который является модальным. Затем правую вершину прямоугольника соединяют с правой вершиной предшествующего прямоугольника, а левую вершину с левой вершиной последующего прямоугольника. Из точки пересечения восстанавливается перпендикуляр до абсциссы – это значение будет модой. Медиана рассчитывается по кумуляте.