7.3.3. Электромагнитные волны.

      Система уравнений Максвелла допускает существование переменного электромагнитного поля в пространстве, свободном от электрических зарядов, в форме электромагнитных волн. Уравнения (7.1) и (7.2) для рассматриваемого случая имеют вид:

     

(7.22)

     

(7.23)

     Вычислим, например, ротор от обеих частей уравнения (7.22):

     

(7.24)

     Из векторного анализа известно, что

     

,

(7.25)

     оператор Лапласа в выражении(7.25) применяется к каждой компоненте векторного поля .

      Из уравнения (7.3) исходной системы уравнений Максвелла для рассматриваемого случая имеем

     

,

(7.26)

     что с учетом уравнения (7.23) позволяет получить

     

.

(7.27)

     В одномерном случае из уравнения (7.27) следует

     

(7.28)

     (для каждой компоненты вектора ).

     Сравнивая уравнение (7.28) с уравнением

     

,

(7.29)

     описывающим распространение бегущей волны с фазовой скоростью вдоль оси, находим, что

     а) каждая из компонент вектора описывается волновым уравнением, т. е. представляет собой волну, бегущую вдоль оси;

     б) фазовая скорость этой волны равна

     

,

(7.30)

      - скорость света (здесь использованы теоретические значения электрической и магнитной постоянных).

     Заметим, что можно было бы провести выкладки, вычисляя ротор от обеих частей уравнения (7.23) и исключая поле из получающегося уравнения с помощью уравнения(7.22). На этом пути приходят к уравнению

     

(7.31)

     Оказывается, что и векторное поле имеет волновой характер, причем фазовая скорость волнысовпадает с фазовой скоростью волны.

      Анализ системы уравнений (7.27) и (7.31) на первый взгляд приводит к выводу, что волны исовершенно независимы друг от друга. На самом деле это не так. Если исследовать решения уравнений(7.22) и (7.23) непосредственно, оказывается, что плоские волны испециальным образом ориентированы друг относительно друга, имеют одну и ту же начальную фазу колебаний и согласованные между собой амплитуды. Частоты и волновые векторы у этих волн одинаковы.

      Интересно, почему система уравнений (7.27), (7.31) не позволяет все это обнаружить? Дело в том, что система (7.27), (7.31) получена из исходных уравнений (7.22)- (7.23) дифференцированием: исходная система - это система двух дифференциальных уравнений первого порядка, а конечная - система двух уравнений второго порядка. Повышение порядка производных в уравнении расширяет класс допустимых решений. Формально независимые волны икак решения системы(7.27), (7.31) содержат, в частности, и такие, которые являются решениями системы (7.22)- (7.23) с описанными выше свойствами, т. е. реальные электромагнитные волны.

      В реальной бегущей электромагнитной волне отличен от нуля средний по времени вектор Умова-Пойтинга

     

(7.32)

     что позволяет говорить о том, что бегущая электромагнитная волна переносит энергию. Среднее по времени значение является плотностью потока импульса, а величина- плотность потока "массы", переносимой электромагнитной волной. Наличие нулевой величины плотности импульса теоретически позволяет рассчитать силу давления, которое оказывает электромагнитная волна на твердую не абсолютно прозрачную поверхность.

      В момент создания системы уравнений Максвелла экспериментально электромагнитные волны не были известны. Их несколько позже обнаружил Г.Герц. Тот факт, что свет является совокупностью электромагнитных волн, стало неоспоримым после знаменитых опытов Лебедева по измерению давления света. Теория электродинамики Максвелла стала общепризнанной.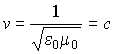