7.2. Основные свойства системы уравнений Максвелла.

     1. Система уравнений Максвелла "замкнута", то есть число неизвестных функций равно числу уравнений в системе.

     2. Система уравнений Максвелла "конструктивна". В математическом анализе доказано, что одновременное задание ротора и дивергенции векторного поля позволяет это поле рассчитать (при выполнении определенных граничных условий). Уравнения (7.1)- (7.4) как раз и задают роторы и дивергенции электрического и магнитного полей, причем ротор электрического поля связан со скоростью изменения магнитного поля, а ротор магнитного поля - со скоростью изменения электрического поля.

     3. Система уравнений Максвелла обладает свойством инвариантности относительно преобразований Лоренца (основа современной теории относительности). Классическая механика Ньютона этим свойством не обладает.

     4. Система уравнений Максвелла удивительно "симметрична" относительно электрических и магнитных величин. Это свойство особенно наглядно проявляется в непроводящей среде в отсутствие объемной плотности свободных электрических зарядов.

7.3. Основные следствия системы уравнений Максвелла

     В настоящем курсе нет возможности рассмотреть все следствия системы уравнений Максвелла, поэтому ниже ограничимся рассмотрением закона сохранения электрического заряда, закона сохранения электромагнитной энергии (теорема Пойтинга) и обсудим некоторые особенности явления распространения электромагнитных волн.

7.3.1. Закон сохранения электрического заряда.

      Закон сохранения электрического заряда неявно содержится в системе уравнений Максвелла. Действительно, вычислим величину дивергенции от правой и левой частей уравнения (7.2)

     

.

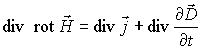      В векторном анализе известен результат (его можно проверить непосредственным вычислением!)

     

.

      Поскольку операция вычисления дивергенции сводится к дифференцированию по пространственным координатам, то порядок вычисления частной производной по времени и вычисления дивергенции можно поменять местами, а если при этом воспользоваться уравнением (7.3), то получим

     

(7.13)

     - закон сохранения электрического заряда в дифференциальной форме (дивергентная форма). Интегральная форма этого закона имеет вид

     

(7.14)

     или в более привычной форме записи

     

.

(7.15)

      Физический смысл полученных интегральных соотношений: в фиксированном объеме величина электрического заряда может измениться только при наличии тока (т.е. движения электрических зарядов) через замкнутую поверхность, ограничивающую этот объем. Закон сохранения электрического заряда в дивергентной форме не содержит объемной плотности источников заряда. Отсюда следует, что в классической электродинамике электрический заряд не может возникнуть и не может исчезнуть.

7.3.2. Теорема Пойтинга.

      Теорема Пойтинга описывает закономерности изменения во времени энергии электромагнитного поля, связанные с излучением энергии в окружающее пространство, диссипацией (джоулево тепло) и мощностью внешних сил.

      Если уравнение (7.1) скалярно умножить на вектор , а уравнение(7.2) скалярно умножить на вектор и из первого уравнения вычесть второе, получим:

     

.

(7.16)

     Непосредственным вычислением можно проверить, что

     

.

(7.17)

      Если электрические характеристики среды постоянны во времени , то

     

.

(7.18)

     Используя полученные результаты, приходим к соотношению:

     

.

(7.19)

     В левой части соотношения (7.19) стоит частная производная по времени от суммы объемных плотностей энергии электрического поля (с этой величиной мы встречались в электростатике) и магнитного поля(с этой величиной мы встречались в магнитостатике), а в правой части - типичный для дифференциальных законов сохранения дивергентный член и объемная плотность "источника" электромагнитной энергии. Для сравнения напомним, что уравнение сохранения электрического заряда не содержало объемной плотности источника зарядов.

      Векторное произведение играет роль плотности потока энергии с размерностью Вт/м². Его обозначают специальным символом и называют вектором Умова-Пойтинга (в зарубежной литературе - вектор Пойтинга). Заметим, что в уравнении баланса энергии электромагнитного поля вектор Умова-Пойтинга появляется только под знаком дивергенции. Это говорит о том, что физический смысл следует приписать выражению, не векторунепосредственно. Интерпретация величины потока векторачерез незамкнутую поверхность всегда требует осторожности.

      С использованием уравнения (7.7) источниковый член в соотношении (7.19) можно переписать в форме

     

,

(7.20)

     где первый член правой части - существенно положительная величина, а знак второго члена правой части зависит от взаимной ориентации векторов и. Первый член представляет собой объемную плотность джоулевых потерь, то есть объемную плотность мощности разогрева среды (Вт/м³). Второй член - это объемная плотность мощности сторонних сил, с этим членом связана возможность либо получения энергии единицей объема среды, либо совершения работы над окружающей средой.

      В интегральной форме соотношение (7.19) имеет вид:

     

,

(7.21)

     где -энергия электромагнитного поля в фиксированном объеме,- мощность джоулева тепловыделения,- мощность сторонних сил. Часто о соотношении(7.21) говорят не как о балансовом соотношении, а как о законе сохранения энергии.