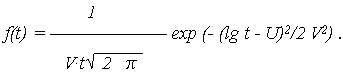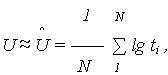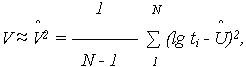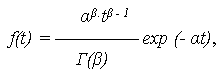7. Виброакустическая диагностика
Виброакустическая диагностика широко используется для оценки состояния роторного оборудования - турбоагрегатов, центробежных насосов и компрессоров, зубчатых передач, двигателей внутреннего сгорания, трубопроводов и запорной арматуры, строительных конструкций. Виброакустическая диагностика НА включает контроль общего уровня виброакустических сигналов агрегата и их спектральный анализ. Контроль за общим уровнем позволяет проводить оценку общего технического состояния и индикацию его критического состояния для предотвращения аварийных ситуаций. Спектральный анализ позволяет уточнить место и характер возникшего дефекта. Рядом исследований установлено, что аффективной оценкой виброакустических спектров обладает спектральная плотность ( спектр ющности), в которой величинами, характеризующими частотные составляющие колебаний, являются квадраты амплитуд, которые характеризуют удельную энергию указан - - и составляющих.
8. Анализ четырех (или более) проб дает возможность установить динамику изменения состава и показателей работоспособности масла в зависимости от времени работы. Если изменения протекают закономерно, двигатель исправен, если обнаружено аномальное изменение одного или нескольких взаимосвязанных показателей – это сигнал тревоги. Диагностическое значение показателей приведено в таблице.
Методы инфракрасного спектрального и феррографического анализа относятся к методам лабораторной трибодиагностики. Они позволяют диагностировать неисправности смазываемых узлов трения. Феррография – метод магнитного осаждения металлических частиц износа из проб смазочного масла. Он позволяет определить вид износа, интенсивность и режимы трения и смазки по форме частиц, состоянию их поверхности, распределению размеров частиц, материалам отдельных частиц, наличию посторонних примесей и продуктов деструкции масла.
Метод феррографии используется не только при исследовании магнитных металлических частиц, но и немагнитных материалов: алюминия, бронзы, латуни, графита, полимерных частиц и т. д. Совокупность этих параметров позволяет идентифицировать вид износа, определить место возможного отказа и оценить степень опасности дефекта. Например, для частиц задира характерны борозды в направлении движения. В случае образования на поверхностях трения усталостных микротрещин при качении в масле появляются сферические частицы. При усталостном выкрашивании образуются хлопьевидные частицы. Обычно на их поверхности имеется множество микроязвин. При коррозионном износе в пробе масла появляется множество частиц размером до 2 мкм. При микрорезании образуются частицы в виде стружки.
9. 1 исследование газового конденсата на кислотность, по содержанию в масле железа моно судить об износе механизмов
11. Законы
распределения наработки до отказа:
экспоненциальный, логнормальный и
гамма-распределение 1.
Экспоненциальное распределение
описывает наработку до отказа объектов,
у которых в результате сдаточных
испытаний (выходного контроля) отсутствует
период приработки, а назначенный ресурс
установлен до окончания периода
нормальной эксплуатации.
Эти объекты
можно отнести к "не стареющим",
поскольку они работают только на участке
с
![]() (t)
=
=
const. Круг таких объектов широк: сложные
технические системы с множеством
компонентов, средства вычислительной
техники и системы автоматического
регулирования и т. п. Экспоненциальное
распределение широко применяется для
оценки надежности энергетических
объектов.
Считается, что случайная
величина наработки объекта до отказа
подчинена экспоненциальному распределению,
если ПРО описывается выражением:
(t)
=
=
const. Круг таких объектов широк: сложные
технические системы с множеством
компонентов, средства вычислительной
техники и системы автоматического
регулирования и т. п. Экспоненциальное
распределение широко применяется для
оценки надежности энергетических
объектов.
Считается, что случайная
величина наработки объекта до отказа
подчинена экспоненциальному распределению,
если ПРО описывается выражением:
f(t) =
|
(1) |
где
–
параметр распределения, который по
результатам испытаний принимается
равным
![]() 1
/
1
/
![]() 0,
где
0
– оценка средней наработки до
отказа.
Остальные показатели
безотказности при известной f(t),
определяются:
0,
где
0
– оценка средней наработки до
отказа.
Остальные показатели
безотказности при известной f(t),
определяются:
вероятность безотказной работы (ВБР): |
P(t) = exp ( - t), |
(2) |
вероятность отказа (ВО): |
Q(t) = 1 - exp ( - t), |
(3) |
интенсивность отказов (ИО): |
(t) = exp ( - t) / exp ( - t) = . |
(4) |
Из (4) следует, что ИО является постоянной величиной, не зависящей от времени, и обратно пропорциональной оценке средней наработки (t) = = 1/ 0 .Числовые характеристики наработки до отказа определяются: - средняя наработка (МО наработки) до отказа
|
(5) |
- дисперсия наработки до отказа
|
(6) |
Графики изменения показателей безотказности при экспоненциальном распределении приведены на рис. 1.
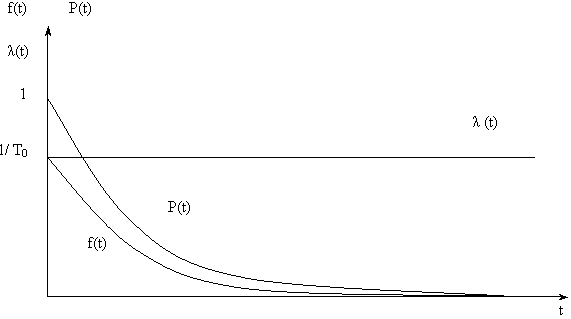
Следует отметить, что при t < < 1, т. е. при наработке t много меньшей, чем средняя наработка T0, выражения (1) – (4) можно упростить, заменив e- t двумя первыми членами разложения e- t в степенной ряд. Например, выражение для ВБР примет вид:
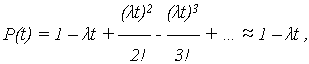
при этом погрешность вычисления P(t) не превышает 0,5 ( t)2. Все рассмотренные далее законы распределения наработки до отказа используются на практике для описания надежности "стареющих" объектов, подверженных износовым отказам. 2. Логарифмически нормальное (логнормальное) распределение При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины T, а не сама эта величина. Логарифмически нормальное распределение во многом более точно, чем нормальное описывает наработку до отказа тех объектов, у которых отказ возникает вследствие усталости, например, подшипников качения, электронных ламп и пр. Если величина lg t имеет нормальное распределение с параметрами: МО U и СКО V, то величина T считается логарифмически нормально распределенной с ПРО, описываемой:
|
(7) |
Параметры U и V по результатам испытаний принимаются:
|
(8) |
|
(9) |
где
![]() и
и
![]() -
оценки параметров U и V.
Показатели
надежности можно рассчитать по приведенным
в лекции 6 выражениям, пользуясь
табулированными функциями f(x) и,
соответственно, F(x) и
-
оценки параметров U и V.
Показатели
надежности можно рассчитать по приведенным
в лекции 6 выражениям, пользуясь
табулированными функциями f(x) и,
соответственно, F(x) и
![]() (x)
для нормального распределения при x =
(lg t - U) / V.
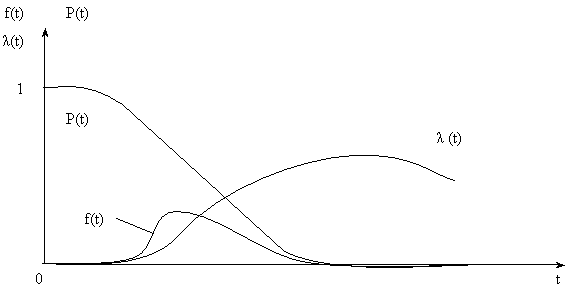
Графики изменения показателей
надежности при логарифмически нормальном
распределении приведены на рис.
2.
Числовые характеристики наработки
до отказа:
(x)
для нормального распределения при x =
(lg t - U) / V.
Графики изменения показателей
надежности при логарифмически нормальном
распределении приведены на рис.
2.
Числовые характеристики наработки
до отказа:
- средняя наработка (МО наработки) до отказа
|
(10) |
- дисперсия наработки до отказа
|
(11) |
3. Гамма–распределение
Случайная величина наработки до
отказа T имеет гамма-распределение с
параметрами
(масштабный
параметр) и
![]() (параметр
формы), где
,
>
0, причем
–
целое число, если ее ПРО описывается
выражением:
(параметр
формы), где
,
>
0, причем
–
целое число, если ее ПРО описывается
выражением:
|
(12) |
где Г( ) = ( - 1)! – гамма-функция Эйлера. Очевидно, что при = 1 выражение (12) упрощается до вида (1), соответствующего экспоненциальному распределению. Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону. При больших гамма-распределение сходится к нормальному распределению с параметрами: a = • , b = • 2. Графики изменения показателей надежности при гамма-распределении приведены на рис. 3. Числовые характеристики наработки до отказа: - средняя наработка (МО наработки) до отказа
T0 = / , (13) |
(13) |
- дисперсия наработки до отказа
D = D{T} = / 2 . |
(14) |

Помимо рассмотренных законов распределения, в качестве моделей надежности объектов могут использоваться и другие, например: распределение Вейбулла, хорошо описывающее наработку объектов до отказа по усталостным разрушениям, распределение Релея, распределение Эрланга и т. п.
1![]() 2.
Определение
параметров закона распределения времени
безотказной работы
Распределение
времени безотказной работы по данным
испытаний и эксплуатации можно оценить
по гистограммам, построенным по
экспериментальным данным о времени
отказов. Отношение высоты каждого
прямоугольника к его ширине будет
определять интенсивность отказов λ(t,
Δt) на соответствующем интервале времени
Δt, отсчитываемом от момента времени t
. В случае, если на испытания поставлены
восстанавливаемые изделия, указанное
отношение будет означать параметр
потока отказов Λ(t, Δt) на соответствующем
интервале времени. Для определенности
далее будем рассматривать параметр
потока отказов. Обработанные таким
образом экспериментальные данные можно
аппроксимировать непрерывной линией
Λ(t) , построенной в соответствии с одним
из известных законов распределения
случайных величин.
Для
определения закона распределения
требуется большой объем статистических
данных. Если закон распределения
определен в результате ранее накопления
данных, то для определения показателей
надежности конкретной партии изделий
объем статистических данных может быть
меньшим.
При
определении закона распределения или
параметров закона распределения
необходимо учитывать число отказов m
за определенные промежутки времени t1
- t . Для вероятности появления данного
числа отказов за указанный промежуток
времени при известной зависимости
параметра потока отказов от времени
существует формула
2.
Определение
параметров закона распределения времени
безотказной работы
Распределение
времени безотказной работы по данным
испытаний и эксплуатации можно оценить
по гистограммам, построенным по
экспериментальным данным о времени
отказов. Отношение высоты каждого
прямоугольника к его ширине будет
определять интенсивность отказов λ(t,
Δt) на соответствующем интервале времени
Δt, отсчитываемом от момента времени t
. В случае, если на испытания поставлены
восстанавливаемые изделия, указанное
отношение будет означать параметр
потока отказов Λ(t, Δt) на соответствующем
интервале времени. Для определенности
далее будем рассматривать параметр
потока отказов. Обработанные таким
образом экспериментальные данные можно
аппроксимировать непрерывной линией
Λ(t) , построенной в соответствии с одним
из известных законов распределения
случайных величин.
Для
определения закона распределения
требуется большой объем статистических
данных. Если закон распределения
определен в результате ранее накопления
данных, то для определения показателей
надежности конкретной партии изделий
объем статистических данных может быть
меньшим.
При
определении закона распределения или
параметров закона распределения
необходимо учитывать число отказов m
за определенные промежутки времени t1
- t . Для вероятности появления данного
числа отказов за указанный промежуток
времени при известной зависимости
параметра потока отказов от времени
существует формула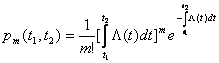 .
(6) В
теории надежности часто применяют закон
распределения Вейбулла
.
(6) В
теории надежности часто применяют закон
распределения Вейбулла
![]() ,
(7) при
котором можно получить уменьшающуюся
со временем интенсивность отказов при
к<1, постоянную при к=0, и увеличивающуюся
с временем при к>1. Этот закон распределения
двухпараметрический, определяется
двумя параметрами Т0В
и k
. В
общем случае закон распределения может
быть многопараметрическим с некоторым
r числом параметров: α1,
α2
, …, αr
. Пусть
в результате опыта за промежуток времени
(t1
, t2)
произошло m событий и требуется определить
точечные оценки
,
(7) при
котором можно получить уменьшающуюся
со временем интенсивность отказов при
к<1, постоянную при к=0, и увеличивающуюся
с временем при к>1. Этот закон распределения
двухпараметрический, определяется
двумя параметрами Т0В
и k
. В
общем случае закон распределения может
быть многопараметрическим с некоторым
r числом параметров: α1,
α2
, …, αr
. Пусть
в результате опыта за промежуток времени
(t1
, t2)
произошло m событий и требуется определить
точечные оценки
![]() 1,
2,
… параметров закона распределения α1,
α2
, … , характеризующих параметр потока
событий Λ(t, α1,
α2
, …). Согласно принципа максимального
правдоподобия [4] значения параметров
распределения должны быть такими, при
которых расчетная вероятность наступления
событий, полученных в опыте, максимальная,
т. е. для каждого параметра αi
должно выполняться условие
1,
2,
… параметров закона распределения α1,
α2
, … , характеризующих параметр потока
событий Λ(t, α1,
α2
, …). Согласно принципа максимального
правдоподобия [4] значения параметров
распределения должны быть такими, при
которых расчетная вероятность наступления
событий, полученных в опыте, максимальная,
т. е. для каждого параметра αi
должно выполняться условие
![]() .
(8) Выбирая
разные интервалы времени (t1i
, t2i)
для каждого i-го параметра αi
на котором имеют место mi
событий, получим систему уравнений для
определения каждого из параметров αi
.Подставляя в (8) выражение (6), после
преобразований можно получить следующую
систему уравнений для нахождения
параметров закона распределения [5]:
.
(8) Выбирая
разные интервалы времени (t1i
, t2i)
для каждого i-го параметра αi
на котором имеют место mi
событий, получим систему уравнений для
определения каждого из параметров αi
.Подставляя в (8) выражение (6), после
преобразований можно получить следующую
систему уравнений для нахождения
параметров закона распределения [5]:
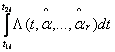 =
mi
, i
= 1,…,r
(9) Если
на испытания поставлены n
восстанавливаемых изделий, то учитывая
увеличение потока отказов в n
раз, последнее выражение приобретает
вид
=
=
mi
, i
= 1,…,r
(9) Если
на испытания поставлены n
восстанавливаемых изделий, то учитывая
увеличение потока отказов в n
раз, последнее выражение приобретает
вид
=
![]() ,
i
= 1,…,r
(10) Для
закона распределения Вейбулла, имеющего
два параметра, из (10) и (7) можно определить
систему уравнений для нахождения
точечных оценок параметров закона
распределения:
,
i
= 1,…,r
(10) Для
закона распределения Вейбулла, имеющего
два параметра, из (10) и (7) можно определить
систему уравнений для нахождения
точечных оценок параметров закона
распределения:
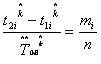 ,
i
= 1, 2 (11) Если
отсчитывать промежутки времени от нуля
– t01
= t02
= 0, то
,
i
= 1, 2 (11) Если
отсчитывать промежутки времени от нуля
– t01
= t02
= 0, то
![]() ;
;
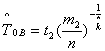 .
(12) 13. Методы
расчёта надёжности
.
(12) 13. Методы
расчёта надёжности
Расчет надежности
на основе классической теории вероятностей
где
![]() —
вероятность безотказной работы элемента
системы.
Наработка
до отказа
системы может быть определена по формуле
—
вероятность безотказной работы элемента
системы.
Наработка
до отказа
системы может быть определена по формуле
![]() Структурные
методы расчета надежности Структурные
методы являются основными методами
расчета показателей надежности в
процессе проектирования объектов,
поддающихся разукрупнению на элементы,
характеристики надежности которых в
момент проведения расчетов известны
или могут быть определены другими
методами. В
качестве структурных схем надежности
могут применяться:
Структурные
методы расчета надежности Структурные
методы являются основными методами
расчета показателей надежности в
процессе проектирования объектов,
поддающихся разукрупнению на элементы,
характеристики надежности которых в
момент проведения расчетов известны
или могут быть определены другими
методами. В
качестве структурных схем надежности
могут применяться:
схемы функциональной целостности;
структурные блок-схемы надежности;
деревья отказов;
графы состояний и переходов.
Логико-вероятностный методВ логико-вероятностных методах (ЛВМ) исходная постановка задачи и построение модели функционирования исследуемого системного объекта или процесса осуществляется структурными и аналитическими средствами математической логики, а расчет показателей свойств надежности, живучести и безопасности выполняется средствами теории вероятностей. ЛВМ являются методологией анализа структурно-сложных систем, решения системных задач организованной сложности, оценки и анализа надежности, безопасности и риска технических систем. ЛВМ удобны для исходной формализованной постановки задач в форме структурного описания исследуемых свойств функционирования сложных и высокоразмерных систем. В ЛВМ разработаны процедуры преобразования исходных структурных моделей в искомые расчетные математические модели, что позволяет выполнить их алгоритмизацию и реализацию на ЭВМ. Общий логико-вероятностный метод Этот подход предусматривает последовательное выполнение следующих четырех основных этапов ОЛВМ:
этап структурно-логической постановки задачи;
этап логического моделирования;
этап вероятностного моделирования;
этап выполнения расчетов показателей надежности.