
Ответы на билеты по выс.математике
.doc|
Билет 1 Ф.м.п., определение, графическое изображение, поверхности и линии уровня. Предел. Непрерывность.
Общ. опред. ф-ии многих переменных. Обл. опред. ф-ии n-перемен. назыв. совокупность точек Rn, для кот. ф-ия имеет смысл. Говорят, что в D задана числов. ф-ия n-переменных f(M) если по з-ну f(M) кажд. т. MD поставл. в соответств. число yE – обл. знач. y=f(x) Бывает, что ф-ии нес-ких перем. зад. с пом. описан., граф., табл. Ф-ии 2 перемен.: z=f(x,y) DR2 z=f(x1,x2) т. M(x,y) y=y(x1,x2) D - совокуп. точек пл-ти Геом. образ. ф-ии 2 перем. – пов-ть в R3 опр.: т. M наз. внутренней т. обл., если она сама и нек. ее окрест. принадлеж. D полностью. Обл. D наз. замкнут. если ей принадл. все внутр. т. границы, в противном случае – обл. D открытая. Ф-ия 3 перемен.: u=f(x,y,z) u=f(x1,x2,x3) обл. опред. – это совокуп. т. в R3. Граф. интерпретац. отсутств. опр.: частичн. приращ. ф-ии: Δxif=f(x1,x2…xi+Δxi, xi+1…xn)-f(x1, x2…xi, xi+1…xn) опр.:
полн. приращ. ф-ии: Δf=f(x1+Δx1,
x2+Δx2…
xn+Δxn)-f(x1,
x2…xn).
Ясно, что
Говорят, что т. M0DRn если для нее вып. нерав-во :
опр.:
число А наз.
M→M0 x1→x10 x2→x20 xn→xn0 опр.: ф-ия f(M0) наз. непрер. в т. М0 если:
как и у ф-ий 1 перем. можно говор. о т. разр. – в кот. наруш. усл. непрер. По аналогии с ф-ей 1 перем. имеет место определение: Ф-ия
непрер. если:
Св-ва ф-ий непрер. на замкн. множ-ве: 1) непрер. ф-ия на замк. множ. достиг. своего наиб. М и наим. m. 2) если М-наиб., m- наим. знач. ф-ии на замкн. множ. D то μ, удовл. нер-ву m<μ<M, хотя бы 1 т. AD, такая что f(A)=μ 3) о корнях непрер. ф-ии: если M>0, m<0 то хотя бы 1 т. AD, такая что f(A)=0 для ф-ии 2 перем.: опр.: линией уров. для ф-ии zx=f(x,y) наз. линия в пл-ти XOY во всех т. кот.знач. ф-ии постоянны, т.е.: f(x,y)=C для ф-ии 3 перем. гов. о пов-ти уров.: пов-тью уров. для ф-ии u=f(x,y,z) наз. пов-ть в R3 во всех т. кот. знач. ф-ии постоянны, т.е.: f(x,y,z)=C
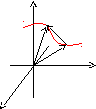
Билет 2 Векторная функция скалярного аргумента. Предел, непрерывность, производная. Геометрический и механический смысл. Нормальное и тангенциальное ускорение.
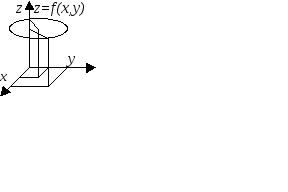
Векторная функция скалярного аргумента.
z
A(x, y, z)
y
х
Пусть некоторая кривая в пространстве задана параметрически: x = (t); y = (t); z = f(t);
Радиус-
вектор произвольной точки кривой:
Таким
образом, радиус- вектор точки кривой
может рассматриваться как некоторая
векторная функция скалярного аргумента
t.
При изменении параметра t
изменяется величина и направление
вектора
Запишем соотношения для некоторой точки t0:
Тогда
вектор
Очевидно, что
Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
или, если существуют производные (t), (t), f(t), то
Это
выражение – вектор производная вектора
Если имеется уравнение кривой: x = (t); y = (t); z = f(t); то в произвольной точке кривой А(xА, yА, zА) с радиус- вектором
можно провести
прямую с уравнением
Т.к.
производная
Определение: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие
также
верно и условие
Записывают:
Определение: Пусть точка М0(х0, у0) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М0(х0, у0), если
причем точка М(х, у) стремится к точке М0(х0, у0) произвольным образом.
Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется по крайней мере одна точка N(x0, y0, …), такая, что для остальных точек верно неравенство f(x0, y0, …) f(x, y, …) а также точка N1(x01, y01, …), такая, что для всех остальных точек верно неравенство f(x01, y01, …) f(x, y, …) тогда f(x0, y0, …) = M – наибольшее значение функции, а f(x01, y01, …) = m – наименьшее значение функции f(x, y, …) в области D. Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.
Производные и дифференциалы функций нескольких переменных.
Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение х к переменной х. Тогда величина xz = f( x + x, y) – f(x, y) называется частным приращением функции по х.
Можно записать
Тогда
Обозначение:
Аналогично определяется частная производная функции по у.
Геометрическим
смыслом частной
производной (допустим
Билет 3 Частные производные и частные дифференциалы ф.м.п
17. Частные приращения и частные производные. Дифференцируемость Ф.М.П. Полный дифференциал, его связь с частными производными. Геометрический смысл полного дифференциала.
о
опр.:
частным приращением функции 2-х
переменных Z=f(x,y)
по Х в точке М
опр.:
Частной производной функции
Г
Билет 4. Полный дифференциал ф.м.п, его приложение, геометрический смысл.
Полное приращение и полный дифференциал.
Определение.
Выражение
Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно х и у приращения функции z в точке (х, у).
Для функции произвольного числа переменных:
Пример.
Найти полный дифференциал функции
Пример.
Найти полный дифференциал функции
Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
N N0
касательная плоскость
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущей NN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
Уравнение нормали к поверхности в этой точке:
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+х, у0+у). Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности
в точке М(1, 1, 1).
Уравнение касательной плоскости:
Уравнение нормали:
Билет 5. дифференцирование сложных ф.м.п.
Дифференцирование сложных функций. Опр. Переменная z=z(t) - называется сложной функцией переменной t, если она определяется равенством: z=z(t)=f[x(t),y(t)] - сложная функция от t. Теорема. Если функция z=f(x,y) дифференцируема в точке р(х, у), а функции x=x(t) и y=y(t) дифференцируемы в ссответствующей точке t, то сложная функция z=z(t) также дифференцируема в точке t и ее производная определяется равенством: dz/dt = z/xdx/dt+ x/ydy/dt [**] Док-во: Дадим переменной t приращение t, при этом х=х(t) получит приращение х, а у=у(t) у, в результате переменная z=f(x,y) получит приращение z, т.к. z(х,у) - дифференцируемая функция, то это приращение может быть представлено в виде: z=z/xx + z/yy + разделим на t и перейдем к пределу Lim(t0)z/t = z/xLim(t0)x/t + + z/yLim(t0)y/t + Lim(t0)/t dz/dt = z/xdx/dt + z/ydy/dt + Lim(t0) //t 0 =x2+y2 Lim(t0)/=0 - по определению дифференциала. Lim(t0)/t = Lim(t0)(x/t)2+(y/t)2= =(dx/dt)2+(dy/dt)2 Формула [**] доказана.
Рассмотрим частный случай сложной функции: z= f[x,y(x)] = z(x) в ф-ле [**] вместо tх, получим dz/dx= z/xdx/dx+ z/ydy/dx dz/dx= z/x+ z/ydy/dx [***] Формула [**] распространяется на сложные функции большего числа переменных. Пусть z=f(x,y), где x=x(r,s,..t), y=y(r,s,..,t) z=z(r,s,..,t) - cложная функция. При этом формула [**] принимает вид: z/r=z/xx/r+x/yy/r z/s=z/xx/s+ z/yy/s [****]
\ Билет 6. Дифференцирование неявных ф.м.п.
Дифференцирование функций, заданных неявно. Опр. Функция z=f(x,y) наз. Заданной неявно, если она определена равенством, неразрешенным относительно z . F(x,y,z)=0 x+y+z=ez - это равенство задаем некоторую функцию z=f(x,y), которую нельзя выразить в полном виде. x2+y2+z2=0 - не задает никакой функции. Теорема: Если ф-я F(x,y,z) непрерывна в т. р0(x0,y0,z0) и ее производная по z Fz(x,y,z)0, то равенство F(x,y,z)=0 однозначно определяет в неявном виде функцию z=f(x,y), при этом эта функция дифференцируема и ее производная находится по формулам: z/x= Fx(x,y,z)/Fz(x,y,z) z/y=Fz (x,y,z)/Fy(x,y,z) Док-во: Найдем полный дифференциал функции dF(x,y,z)=F/x*dx+F/y*dy+F/x*dz F(x0,y0,z0)=0dF=0 F/x*dx+F/y*dy+F/x*dz=0 dz=(F/x)/(F/z)*dx(F/y)/(F/z)*dy (*) С другой стороны: z=f(x,y), dz=z/x*dx+z/y*dy (**) Сравнивая (*) и(**) z/x= Fx(x,y,z)/Fz(x,y,z) z/y=Fz (x,y,z)/Fy(x,y,z)
Билет 7. Касательная плоскость и нор к поверхности.
Геометрический смысл полного дифференциала. Касательная плоскость и нормаль к поверхности.
нормаль
N N0
касательная плоскость
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущей NN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
Уравнение нормали к поверхности в этой точке:
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+х, у0+у). Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности
в точке М(1, 1, 1).
Уравнение касательной плоскости:
Уравнение нормали:
Билет 8. Условный экстремум ф.м.п. наибольшее и наименьшее значение в ограниченной замкнутой области.
Условный экстремум.
Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение (х, у) = 0, которое называется уравнением связи. Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи. Тогда u = f(x, y(x)).
В точках экстремума:
Кроме того:
Умножим равенство (2) на число и сложим с равенством (1).
Для выполнения этого условия во всех точках найдем неопределенный коэффициент так, чтобы выполнялась система трех уравнений:
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум. Выражение u = f(x, y) + (x, y) называется функцией Лагранжа.
Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи: 2x + 3y – 5 = 0
Таким
образом, функция имеет экстремум в
точке
Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа. Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется по крайней мере одна точка N(x0, y0, …), такая, что для остальных точек верно неравенство f(x0, y0, …) f(x, y, …) а также точка N1(x01, y01, …), такая, что для всех остальных точек верно неравенство f(x01, y01, …) f(x, y, …) тогда f(x0, y0, …) = M – наибольшее значение функции, а f(x01, y01, …) = m – наименьшее значение функции f(x, y, …) в области D. Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.
Билет 9. Производная по направлению. Скорость наибольшего возрастания функции. Градиент. Крутизна поверхности
Производная по направлению.
Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М1( x + x, y + y, z + z).
Проведем через
точки М и М1
вектор
Расстояние
между точками М и М1
на векторе
Высказанные выше предположения, проиллюстрируем на рисунке: z
M1
y
x
Далее предположим, что функция u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:
где
величины 1,
2,
3
– бесконечно малые при
Из геометрических соображений очевидно:
Таким образом, приведенные выше равенства могут быть представлены следующим образом:
Заметим,
что величина s
является скалярной. Она лишь определяет
направление вектора
Из этого уравнения следует следующее определение:
Определение:
Предел
( x, y, z).
Поясним значение изложенных выше равенств на примере.
Пример.
Вычислить производную функции z
= x2
+ y2x
в точке А(1, 2) по направлению вектора
Решение.
Прежде всего необходимо определить
координаты вектора
Далее определяем модуль этого вектора:
Находим частные производные функции z в общем виде:
Значения
этих величин в точке А :
Для
нахождения направляющих косинусов
вектора
За
величину
Отсюда
получаем значения направляющих
косинусов вектора
cos
=
Окончательно
получаем:
Градиент.
Определение: Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке
то этот вектор называется градиентом функции u.
При этом говорят, что в области D задано поле градиентов.
Билет 10 уравнение первого порядка. Общее, частное, особое решение. Метод изоклин. Задача Коши. Д.у. с разделяющимися переменными
Дифференциальные уравнения первого порядка. Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если
такое соотношение преобразовать к
виду
Преобразуем такое выражение далее:
Функцию
f(x,y)
представим в виде:
- это так называемая дифференциальная форма уравнения первого порядка. Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения вида y’ = f(x). Пусть функция f(x) – определена и непрерывна на некотором интервале
a
< x
< b.
В таком случае все решения данного
дифференциального уравнения находятся
как
2. Метод изоклин
Данный метод
является одним из наиболее широко
используемых графических методов
приближенного интегрирования. Он
непосредственно используется для
решения уравнений первого порядка
вида
в плоскости
вдоль каждой
изоклины наносятся черточки с
наклоном, определяемым соответствующим
значением
от точки
Задача Коши для уравнения первого порядка.
Как уже было сказано, общим решением уравнения (16.2) является все множество функций, обращающих при подстановке рассматриваемое уравнение в тождество. Пусть теперь требуется найти решение этого уравнения, удовлетворяющее условию у (х0) = у0 , (16.3) называемому начальным условием. Если общее решение уравнения (16.2) задается формулой у = φ (х, С), (16.4) то значение постоянной С, соответствующее поставленному начальному условию, можно определить, подставив в равенство (16.4) х = х0 и у = у0.
Определение 16.3. Задача выбора из общего решения (16.4) уравнения (16.2) решения, удовлетворяющего начальному условию (16.3), называется задачей Коши, а выбранное решение называется частным решением уравнения (16.2).
Замечание. Если воспринимать множество всех решений уравнения (16.2) как множество интегральных кривых на плоскости, то ставится задача поиска той из них, которая проходит через точку с координатами (х0 , у0). Выясним, при каких условиях такая кривая существует и является единственной.
Уравнения с разделяющимися переменными.
Дифференциальные уравнения вида f2(y)dy = f1(x)dx (17.1) называются уравнениями с разделяющимися переменными. Тогда любое решение у(х) этого уравнения будет удовлетворять и уравнению
где с – произвольная постоянная. Если удается найти первообразные функций f1(x) и f2(y), выраженные в элементарных функциях, то из (17.2) можно получить конечное уравнение вида Ф (х , у) = 0, (17.3) которое определяет решение у(х) уравнения (17.1) как неявную функцию х. Определение 17.1. Уравнение вида (17.3) называется интегралом уравнения (17.1), а если оно определяет все решения (17.1) – общим интегралом этого уравнения.
Пример.
Если требуется найти частное решение уравнения (17.1), удовлетворяющее условию у(х0)=у0 , достаточно подставить значения х0 и у0 в уравнение (17.3) и найти значение с, соответствующее начальному условию.
Пример. Найти решение уравнения y′ctg x + y = 2, удовлетворяющее условию у(0) = -1. Разделим
переменные:
2 – y = c• cos x. Подставив в это равенство х = 0 и у = -1, получим, что с = 3. Следовательно, искомое частное решение имеет вид: y = 2 – 3cos x.
Билет 11. Однородные дифференциальные уравнения 1 порядка, приводящиеся к ним. Их решение.
4. Однородное дифференциальное уравнение первого порядка.
Функция f(x,y)
называется однородной степени m,
если
Функция f(x,y)
называется однородной нулевой степени,
если
Например, функция
Всякая однородная
функция нулевой степени может быть
представлена в виде функции от отношения
y/x
(или отношения x/y).
Действительно, пусть f(x,y)
– однородная функция нулевой степени,
тогда, взяв в качестве
Определение.
Дифференциальное уравнение первого
порядка F(x,y,y/)=0,
называется однородным, если оно может
быть представлено в виде y/=f(x,y)
или
Решение однородного дифференциального уравнения сводится к решению уравнения с разделяющимися переменными заменой y/x=u или y=ux, где u-функция от x.
Подставляя в
исходное уравнение
Пример 1. Рассматривается уравнение (x2-y2)dx+2xydy=0.
Перепишем его в
виде
Разделяя переменные приходим к уравнению
Интегрируем левую и правую части этого уравнения:
Приравнивая найденные интегралы, получаем общее решение вспомогательного дифференциального уравнения относительно переменных x и u
Потенциируя
последнее выражение, общее решение
получает вид
Заменяя u=y/x,
получаем общий интеграл исходного
дифференциального уравнения
Последнее выражение приводится к виду
Таким образом,
семейством интегральных кривых
исходного уравнения является семейство
окружностей с центрами в точках
Пример 2. Требуется
найти частное решение уравнения
Удовлетворяющих начальному условию y(1)=0. Нетрудно видеть (убедиться), что справа стоит однородная функция нулевой степени. Итак, исходное дифференциальное уравнение является однородным. Выполняя замену y=ux, приводим его к виду
Разделяем переменные, получаем
Интегрируя обе части этого уравнения, получаем общее решение вспомогательного дифференциального уравнения
Подставим в него
Последнее
соотношение дает общее решение
исходного дифференциального уравнения.
Чтобы найти частное решение, воспользуемся
начальными условиями x=1,y=0.
Подставим их в общее решение
Таким образом,
искомое частное решение имеет вид
Билет 12. Линейные однородные и неоднородные дифференциальные уравнения 1 порядка. Метод подстановки и метод Лагранжа решения линейных неоднородных дифференциальных уравнений 1 порядка.
Линейное дифференциальное уравнение первого порядка. Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида y/+g(x)y=h(x). Такое название ему дано в связи с тем, что относительно переменных y и y/ его можно рассматривать как линейное.
Если
Если
Его общее решение
имеет вид
Предположим
теперь, что
Представим исходное уравнение в виде
и подставим в
выражение, стоящее в квадратных
скобках,
являясь линейным однородным дифференциальным уравнением (в нем вместо y взята для удобства переменная z, чтобы не возникло путаницы решений этого уравнения с исходным). Общее решение этого уравнения, как уже отмечалось ранее, может быть представлено в виде
где A
– произвольная постоянная. Очевидно,
Если теперь
освободиться от условия фиксирования
постоянной
В нем второй
множитель функция
Действительно, подставляя в это уравнение u/x(x,c), получаем тождество
Таким образом,
показано, что общее решение линейного
дифференциального уравнения
Представляется
в виде y=u(x,c)v(x),
где v(x)
– частное решение однородного уравнения
Нетрудно видеть, что в обоих случаях приходится решать уравнение с разделяющимися переменными.
Заметим, что хотя
при решении однородного уравнения
Являющегося уравнением с разделяющимися переменными. На втором этапе определяется решение u(x,c) дифференциального уравнения u/v(x)=h(x), Также являющегося уравнением с разделяющимися переменными. После их решений общее решение исходного линейного уравнения представляется в виде Y=u(x,c)v(x). Пример 1. Решить уравнение Y/+2y=sinx. Сначала решаем однородное уравнение v/+2v=0. Из него получаем
Интегрируя его левую и правую части, получаем его общий интеграл (решение) вида
Полагая в нем c=0
и потенциируя его, получаем следующее
его нетривиальное частное решение
Далее решаем уравнение вида
Разнося переменные в разные части уравнения и интегрируя их, получаем общее решение этого уравнения
Вычислим интеграл:
Рассматривая данное уравнение, как уравнение относительно интеграла, находим его вид
Следовательно,
Тогда общее решение исходного уравнения будет
Предположим теперь, что требуется выделить частное решение, проходящее через точку M(0,0), т.е. решение, удовлетворяющее начальному условию y(0)=0. Для этого подставим значения x=0, y=0 в общее решение и найдем соответствующее значение постоянной c:
Искомым частным решением является
Пример 2. Решить уравнение
являющееся линейным дифференциальным уравнением. На первом этапе найдем решение соответствующего линейного однородного уравнения
Разделяя переменные по разные стороны уравнения, имеем
Интегрируя обе части данного уравнения, получаем следующее его частное решение
На втором этапе решаем уравнение вида
Делая замену
Интегрируя правую и левую части уравнения, получаем его общее решение
Общее решение исходного дифференциального уравнения имеет вид
Метод Лагранжа (дифференциальные уравнения) Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения anz(n) + an − 1z(n − 1) + ... + a1z' + a0z = f(t) состоит в замене произвольных постоянных ck в общем решении z(t) = c1z1(t) + c2z2(t) + ... + cnzn(t) соответствующего однородного уравнения anz(n) + an − 1z(n − 1) + ... + a1z' + a0z = 0 на вспомогательные функции ck(t), производные которых удовлетворяют линейной алгебраической системе
Определителем
системы (1) служит вронскиан
функций z1,z2,...,zn,
что обеспечивает её однозначную
разрешимость относительно
Если
является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам..
|
Билет 14ДУ_высших порядков_ допускающие понижение порядка. Рассмотрим дифференциальное уравнение п-го порядка: F (x, y, y′,…, y(n)) = 0, (1) где F предполагается непрерывной функцией всех своих аргументов. О: Соотношение следующего вида: у(п) = f (x, y, y′,…, y(n-1)) …называется ДУ разрешенным относительно высшей производной. О: Всякое ДУ порядка выше 1-ого называется ДУ высшего порядка. О:
Начальными
условиями при х=х0
наз. значение функции у и всех ее
производных до n-1
включительно: О:
Функция у=u(x)
называется решением ДУ (1) и (2), если
она удволетворяет начальным условиям:
О:
Ф-ия
Решения, получающиеся из общего при конкретных значениях с1, с2 и т. д. называются частными решениями ДУ (1) и (2). Если эта ф-я есть общее решение ДУ () и (), то частные решения получаются из общего путем определения постоянных с1, С2 и т. д. из системы:
y0 = (x0, C1, C2, ……., Cn) Эта система с n неизвестными C1, C2, ……., Cn y0’ = ’( x0, C1, C2, ……., Cn) (4) Найдя их значения и подставив в общее _ _ _ _ _ _ _ _ _ _ _ _ _ _ решение получим частные решения, например: y0(n-1) = (n-1)( x0, C1, C2, ……., Cn) y = (x, C10, C20, ……., Cn0) ___________________________________________________________________________ В
некоторых случаях порядок дифференциального
уравнения может быть понижен, что
обычно облегчает его интегрирование.
Рассмотрим несколько типов подобных
уравнений. 1.Уравнение не содержит
искомой функции и ее производных по
порядок (k
– 1) включительно:
Порядок такого уравнения можно понизить на единицу заменой у′ = р(у). При этом производные функции f(x) по аргументу х нужно выразить через производные р по у:
Билет 15 ЛОДУ_с постоянными коэфициентами.
ЛОДУ-уравнение
вида:
называется характеристическим уравнением для уравнения (1). Числа k, являющиеся его решениями. Исследуем различные возможности количества и вида решений характеристического уравнения.
3. Характеристическое уравнение имеет кратные корни. В этом случае число линейно независимых решений предыдущих типов меньше п, и для получения фундаментальной системы нужно найти дополнительные решения иного вида.
В этом случае
каждый кратный корень уравнения (2)
задает серию линейно независимых
частных решений уравнения (1), количество
которых равно его кратности. Таким
образом общее решение уравнения (1)
можно записать в виде
Билет 16 ЛОДУ с переменными коэффициентами. ДУ
вида
P1(x), P2(x)….Pn(x), которые есть непрерывные ф-ии на некотором интервале [a:b] Назовем линейным дифференциальным оператором
Гипотеза: Операясь на свойства L(y) можно предположить, что любая линейная комбенация частных решений y1, y2, ………yn и c1y1+c2y2+……+cnyn (2) есть также решения ДУ(1). Выражение вида (2) можно было бы считать общим решением ДУ (1) если бы знать что все y1, y2, ………yn линейно независимы. y1, y2, ………yn называются линейно независимыми если справедливо следуюющее тождество c1y1+c2y2+……+cnyn =0 (*) но только если все С=0 О: Система функций называется линейно независимой если тождество (*) справедливо но не когда все Cn=0 т. е. Среди них есть отличные от нуля. Определить линейную независимость поможет определитель Вронского, который представляет собой выражение вида:
Если W(x) неравно 0 то система y1, y2, ………yn будет линейно независимой т. е. Их линейная комбинация c1y1+c2y2+……+cnyn =0 только в том случае когда С1=С2=0 О: Система n линено независимых решений ДУ(1) называется его фундаментальной системой. Т: Для того чтобы n решений ДУ (1) y1, y2, ………yn составляли его фундаментальную систему необходимо и достаточно, чтобы их определитель Вронского был отличен от 0. Если y1, y2, ………yn есть какая-либо фундаментальная система решений ДУ(1), то линейная комбенация этих решений с n произвольными параметрами С1, С2, ………Сn есть общее решение ДУ(1). у= c1y1+c2y2+……+cnyn П: у”+y=0 Очевидно что у=cosx и у=sinx будут его частными решениями т.к. W(x)<>0 Следовательно у=С1cosx +С2sinx Билет 17 ЛОДУ 2-ог порядка с переменными коэффициентами Это уравнение вида y”+P1(x)y’+P2(x)y=0 . Можно решить это уравнение подбором, т.е. эвристически найти фундаментальные системы решения. Найти подбором 2 и более частных решений не всегда удается, поэтому существует еще один способ, но для его реализации должно быть уже найдено 1 частное решение, тогда 2 решение можно будет найти по определенной формуле. Т: Для уравнения y”+P1(x)y’+P2(x)y=0 определитель Вронского можно записать через коэффициенты, т.е. W(x)=C*exp(-P(x)dx) Следствие из Т: Если известно что частное решение уравнения будет y то 2 частное решение y2 линейно независимое с y1 найдется по следующей формуле:
До-во: y”+(2y’)/(x)+y=0, y1=(cosx)/x 1)
P1(x)=2/x
Найдем y2
Билет 18 ЛНДУ с переменными коэффициентами
О: Линейное
неоднородное ДУ n-ого
порядка с переменными коэффициентами
называется ДУ следующего вида
L(y)=F(x) L(y)-линейный дифференциальный оператор Т: Сумма общего решения однородного уравнения и какого либо частного решения неоднородного уравнения есть общее решение неоднородного уравнения, т.е. Уон=Уоо+Учн Алгоритм возможного решения:
1. Решаем
соответствующее однородное Ду
т.е.
Уоо=С1У1+С2У2+…..+СnУn 2. Затем нужно найти какое-либо частное решение неоднородого ДУ (1)(чаще всего это делается подбором) 3. Окончательное общее решение неоднородного уравнения. Уоо=С1У1+С2У2+…..+СnУn+Учн=Уоо+Учн
П: Рассмотрим Ду
2-ого порядка
Метод называется методом варьирования произвольной постоянной в соответствующем данному однородном ДУ
Алгоритм:
(4) С1(х)У1 + С2(х)У2=0 С1’(х)У1'+ С2’(х)У2’= F(x)
Т У=С1(х)У1+С2(х)У2 Р2(х) У=С1(х)У1+С2(х)У2 Р1(х) У=С1(х)У1+С2(х)У2 1 Получим: L(y)=C1(х)L(y1)+ C2(х)L(y2)+f(х) (6) Но L(y1=L(y2)=0, т.к. у1 и у2 есть решения ДУ (3) поэтому ур (6) перепишется L(y)=f(x), а это и есть(2). Отсюда ф-ия (*) есть общее решение (2) при условиях (4) из которых можно найти С1(х) и С2(х) Определитель (4) есть определитель Бронского от у1 и у2 (здесь они постоянные а С1’(х) и С2’(х)-искомые). По формулам крамера находим С1’(х) и С2’(х) С1’(х)=W1(x)/W(x); С2’(х)= W2(x)/W(x); С1 (х)= (W1(x)/W(x))dx+C1; С2’(х)= (W2(x)/W(x))dx+C2
Уон=( (W1(x)/W(x))dx+C1)у1+( (W2(x)/W(x))dx+C2)у2= у1 (W1(x)/W(x))dx+ +у2 (W2(x)/W(x))dx+ С1У1+С2У2= Уоо+Учн
ЛНДУ с постоянными
коэффициентами. Т: Сумма общего решения однородного уравнения и какого либо частного решения неоднородного уравнения есть общее решение неоднородного уравнения, т.е. Уон=Уоо+Учн Уоо находится по характеристическому уавнению:
1. k1,
k2,…,
kn
:
2.
3.
Характеристическое уравнение имеет
кратные корни:
Для некоторых
видов правой части линейного
неоднородного дифференциального
уравнения
(1) можно подобрать частное решение в виде функции с неопределенными коэффициентами, которые определяются путем подстановки этой функции в уравнение (1).
б) если p ± qi - корни характеристического уравнения кратности α, то
Пример.
Для уравнения
Билет 20 Дифференциальные уравнения свободных колебаний
Спроектируем уравнение движения на ось X, при этом учтем, что сила упругости пропорциональна смещению из положения равновесия и направлена в сторону ему противоположную, а ускорение - это вторая производная координаты по времени. Тогда:
Преобразуем выражение (1) к виду
Введем
обозначение
Выражение (2) - это дифференциальное уравнение свободных гармонических незатухающих колебаний.Решение уравнения (2) будем искать в виде:
Подставим (3) в (2) получим
Из
полученного выражения найдем значения
где
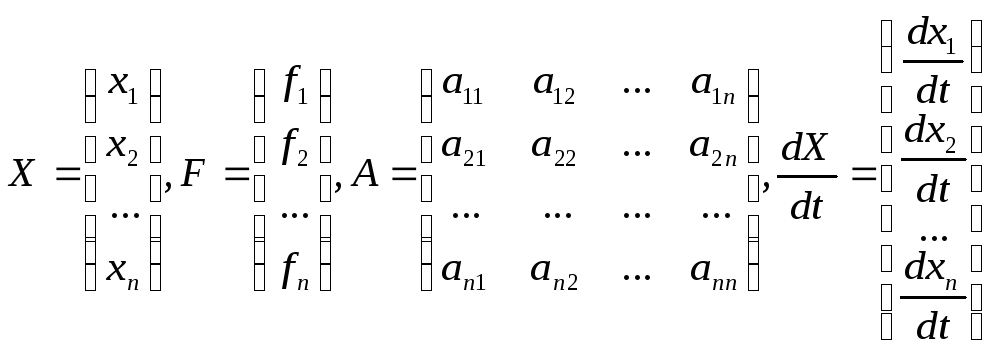
Билет 23 _системы линейных уравнений О. Система дифференциальных уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных. В частности, система линейных уравнений первого порядка с постоянными коэффициентами имеет вид:
. Тогда системе
(1) эквивалентно матричное уравнение
Так как оператор L обладает свойствами линейности:
то для решений линейной однородной системы (3) (при F = 0) справедливы те же свойства: если Х1 и Х2 – решения однородного уравнения (3) , то и их линейная комбинация будет решением того же уравнения. Можно ввести понятие линейной зависимости решений Х1, Х2,…, Хп: О: Х1, Х2,…, Хп , где
Замечание. Назовем определителем Вронского для уравнения (23.4) определитель вида
являющийся определителем системы уравнений, получаемых при координатной записи равенства (23.4). Можно показать, что так же, как и в случае решения линейного однородного уравнения, при W = 0 решения Х1, Х2,…, Хп линейно зависимы на [a,b]. Тогда справедлива следующая теорема:
Теорема 23.1.
Линейная комбинация
однородной системы является общим решением этой системы. Будем искать фундаментальную систему решений линейной однородной системы с постоянными коэффициентами
в виде:
где αi – постоянные. Подставив (23.7) в (23.6) и сократив на ekt, получим:
Для того, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы ее главный определитель был равен нулю:
что представляет
собой уравнение п
– й степени относительно k,
называемое характеристическим.Если
все корни характеристического уравнения
различны, то, подставляя их последовательно
в систему (23.8), можно найти соответствующие
им значения
где ci – произвольные постоянные.
Следовательно,
общее решение системы имеет вид:
В случае кратных корней характеристического уравнения решение системы (23.6) имеет вид
Замечание. Для неоднородной системы (23.1) общим решением, так же как для неоднородного уравнения, будет сумма общего решения соответствующей однородной системы и частного решения неоднородной системы. При подборе частных решений справедлив принцип суперпозиции. Билет 24 Кратные интегралы Р
Пусть
в области D
задана функция z
= f(x,
y).
Обозначим через f(P1),
f(P2),…,
f(Pn)
значения этой функции в выбранных
точках и составим сумму произведений
вида f(Pi)ΔSi
:
О:.
Сумма вида
Замечание.
С геометрической точки зрения (при
Определение
7.2. Если
существует один и тот же предел
интегральных сумм (7.1) при
Область D при этом называется областью интегрирования.
Замечание 1. Для выяснения вопроса об условиях интегрируемости функции двух переменных можно по аналогии со случаем определенного интеграла ввести понятие верхней и нижней интегральных сумм, выбирая в каждой части области D точки, значение функции в которых является наибольшим и наименьшим для данной части. Тогда можно доказать, что необходимым и достаточным условием интегрируемости функции f(x, y) является, во-первых, ее ограниченность на D, а во-вторых, условие
где τ – некоторое разбиение, а Sτ и sτ – соответственно верхняя и нижняя интегральные суммы. Замечание 2. если функция f(x, y) непрерывна на D, то она интегрируема по этой области. Тройной интеграл.
Понятие тройного (а в дальнейшем – т-мерного) интеграла вводится по аналогии с двойным интегралом. Пусть
в пространстве задана некоторая
область V,
ограниченная замкнутой поверхностью
S.
Зададим в этой замкнутой области
непрерывную функцию
f(x,
y,
z).
Затем разобьем область V
на произвольные части Δvi
, считая
объем каждой части равным Δvi
, и составим интегральную сумму вида
где точка Pi принадлежит Δvi . Пусть ρ – наибольшее расстояние между двумя точками любой части области V.
Определение
7.3. Предел
при
Замечание 1. Условие непрерывности подынтегральной функции не является обязатель-ным для существования кратного (двойного, тройного и т.д.) интеграла, но исследование вопросов, связанных с интегрированием разрывных функций, выходит за рамки нашего курса. Замечание 2. Все сформулированные ранее свойства двойного интеграла можно распространить на тройной интеграл. Замечание 3. Подобным образом можно дать определение интеграла любой кратности, рассматривая функцию п переменных, заданную в замкнутой области п-мерного пространства. Разберем вычисление кратных интегралов на примере тройного интеграла. Назовем трехкратным интегралом от функции f(x, y, z) по области V выражение вида:
Трехкратный и двукратный интеграл обладают одинаковыми свойствами:
Т: Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу по той же области:
Замечание: изменение порядка интегрирования не меняет значения трехкратного и двукратного интегралов. Пример.
Вычислим интеграл
точках (0, 0, 0), (1, 0, 0), (0, 1, 0) и (0, 0, 1). Ее проекцией на плоскость Оху является треугольник с вершинами (0, 0), (1, 0) и (0, 1). Снизу область ограничена плоскостью z = 0, а сверху – плоскостью x + y + z = 1. Перейдем к трехкратному интегралу:
Билет № 25. Наиболее часто к замене переменной в тройном интеграле прибегают с целью перейти от декартовой прямоугольной системы координат к цилиндрической или сферической системе. См. Цилиндрическая и сферическая системы координат. Рассмотрим эти преобразования подробнее.
Цилиндрическая система координат.
Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:
Итого:
Билет № 26. Сферическая система координат.
Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
Для представления тройного интеграла в сферических координатах вычисляем Якобиан:
Окончательно получаем:
Билет 27 _Геометрические приложения кратных интегралов Двойной интеграл.
где ΔDi
– проекция
ΔSi
на плоскость Оху,
γ – угол между осью Оz
и нормалью к ΔSi
в некоторой ее точке
и устремив ее к
пределу при
Тройной интеграл. 1. Объем тела. Из определения 7.3 следует, что при f(x, y, z) ≡ 1 тройной интеграл по некоторой замкнутой области V равен объему тела V:
2. Масса тела. Если γ = γ (x, y, z) – функция, задающая плотность вещества, из которого состоит тело V, то масса тела выражается формулой
Билет 28 Механические приложения кратных интегралов Двойной интеграл Момент инерции плоской фигуры.Вспомним определение момента инерции а) материальной точки М с массой т относительно точки О: I = mr² (r – расстояние от М до О);
б) системы
материальных точек m1,
m2,…,
mn
относительно точки О:
Определим теперь момент инерции относительно точки О материальной плоской фигуры D.
ΔSi D
ri
Рис. 1. Найдем момент инерции фигуры D (рис.1) относительно начала координат, считая, что плотность в каждой точке равна 1. Разобьем область D на части ΔSi (i = 1, 2,… n) и выберем в каждой части точку Pi (ξi, ηi). Назовем элементарным моментом инерции площадки ΔSi выражение вида ΔIi = (ξi² + ηi²)ΔSi и составим интегральную сумму
для функции f(x, y) = x² + y² по области D.
О:.
Предел
интегральной суммы (14.4) при
О:.
Интегралы (3) называются моментами инерции фигуры D относительно осей Ох и Оу.
Замечание.
Если поверхностная плотность не равна
1, а является некоторой функци-ей γ
= γ(х, у), то
момент инерции фигуры относительно
начала координат вычисляет-ся по
формуле Координаты центра масс плоской фигуры. Как известно, координаты центра масс системы материальных точек P1, P2,…, Pn с масса-ми т1, т2,…, тп определяются по формулам
Если разбить плоскую фигуру D с поверхностной плотностью, равной 1, на части, то масса каждой части будет равна ее площади. Будем считать теперь, что вся масса эле-ментарной площадки ΔSi сосредоточена в какой-либо ее точке Pi (ξi, ηi). Тогда фигуру D можно рассматривать как систему материальных точек, центр масс которой определяется равенствами
Переходя
к пределу при
В случае переменной поверхностной плотности γ = γ (х, у) эти формулы примут вид
Тройной интеграл
Используя формулы для моментов инерции точки М (x, y, z) массы т относительно координатных осей:
и проводя те же рассуждения, что и при определении моментов плоской фигуры, можно задать моменты инерции тела относительно координатных осей в виде:
где γ (х, y, z) – плотность вещества.
Формулы для координат центра масс тела тоже задаются аналогично случаю плоской фигуры:
Билет № 29. Криволинейные интегралы первого и второго рода, его приложения(длина дуги, масса кривой, моменты инерции кривой, координаты центра масс кривой)
Рассмотрим на
плоскости или в пространстве кривую
L
и функцию f,
определенную в каждой точке этой
кривой. Разобьем кривую на части Δsi
длиной Δsi
и выберем
на каждой из частей точку Mi.
Составим интегральную сумму
Определение
10.1. Если
существует конечный предел интегральной
суммы
Криволинейный интеграл 1-го рода.
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
3. Моменты кривой
l
найдем, рассуждая так же, как в случае
плоской области:
4.Координаты центра масс кривой вычисляются по формулам
Билет №30. Вычисление криволинейного интеграла первого рода при различном задании области определения(дуги кривой). Свойства криволинейного интеграла первого рода. Свойства криволинейного интеграла 1-го рода:
Справедливость этих свойств следует из определения криволинейного интеграла 1-го рода.
Способ вычисления криволинейного интеграла 1-го рода.
Выберем на кривой
L
направление от начальной точки А
и отметим, что положение точки М
на кривой определяется длиной дуги
АМ = s.
Тогда кривую L
можно задать параметрически: x
= x(s),
y
= y(s),
z
= z(s),
где
где
Если же кривая L задана в параметрической форме: x = φ(t), y = ψ(t), z = χ(t), t0 ≤ t ≤ T, то, применяя в интеграле (10.3) формулу замены переменной и учитывая, что дифференциал дуги
получим:
Таким образом, вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции переменной t в пределах, соответствующих изменению значения этой переменной на рассматриваемой кривой.
Билет№31. Криволинейный интеграл второго рода. Задача о работе силового поля .Интеграл в декартовой и векторной форме.
Вновь рассмотрим
кривую L,
в каждой точке которой задана функция
f(M),
и зададим разбиение кривой на отрезки.
Выберем на каждом отрезке точку Mi
и умножим значе-ние функции в этой
точке не на длину i-го
отрезка, как в случае криволинейного
инте-грала 1-го рода, а на проекцию
этого отрезка, скажем, на ось Ох,
то есть на разность xi
– xi-1
= Δxi.
Составим из полученных произведений
интегральную сумму
Определение
10.2. Если
существует конечный предел при
Подобным образом можно определить и криволинейные интегралы 2-го рода вида
Определение 10.3. Если вдоль кривой L определены функции P(M) = P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y, z) и существуют интегралы
то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают
Замечание. Если
считать, что сила
то есть криволинейным интегралом 2-го рода.
Свойства криволинейного интеграла 2-го рода.
Действительно, при этом изменяется знак Δxi в интегральной сумме.
Способ вычисления криволинейного интеграла 2-го рода.
Теорема 10.1. Пусть кривая L задана параметрическими уравнениями x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β , где φ, ψ, χ – непрерывно дифференцируемые функции, и на ней задана непрерывная функция f(x, y, z). Тогда интеграл (10.5) существует и имеет место равенство
Доказательство. Запишем Δxi = xi – xi-1 = φ(ti) – φ(ti-1) и преобразуем последнюю разность по формуле Лагранжа: φ(ti) – φ(ti-1) = φ΄(τi)Δti, где τi – некоторое значение t, заключенное между ti-1 и ti. Выберем точку Мi так, чтобы ее координаты соответствовали значению параметра, равному τi : Mi(φ(τi), ψ(τi), χ(τi)). Подставив эти значения в формулу (10.5), получим:
Справа получен предел интегральной суммы для функции f(φ(t),ψ(t),χ(t))φ΄(t) на отрезке [α, β], равный определенному интегралу от этой функции:
что и требовалось доказать.
Следствие.
Аналогичные соотношения можно получить
для криволинейных интегра-лов вида
Билет № 32. Криволинейный интеграл второго рода по замкнутому контуру. Формула Грина. Независимость криволинейного интеграла 2-го рода от пути интегрирования.
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярное или векторное). Рассмотрим некоторые характеристики скалярных и векторных полей.
Определение 11.1. Если в некоторой области задано скалярное поле U(x,y,z), то поверхность, определяемая уравнением U(x, y, z) = C, (11.1) называется поверхностью уровня. В двумерном случае линия уровня задается уравнением U(x, y) = C. (11.1`)
Определение
11.2. Если в
некоторой области задано векторное
поле
Поверхность, составленная из векторных линий, называется векторной поверхно-стью. Если векторная поверхность образована векторными линиями, проходящими через каждую точку некоторой замкнутой кривой, то она называется векторной трубкой.
Определение 11.3. Пусть задано скалярное поле U(x, y, z). Вектор
называется градиентом величины U в соответствующей точке (см. лекцию 4 за 2-й семестр). Замечание. Таким образом, скалярное поле U(x, y, z) порождает векторное поле градиента gradU.
Определение
11.4. Пусть
дано векторное поле
называется
линейным
интегралом от вектора
Здесь
Замечание. Иногда
криволинейный интеграл 2-го рода по
замкнутому
контуру обозначают
Пример. Вычислить
циркуляцию векторного поля
x² + y² = 9, z = 2 (направление обхода контура – от точки (3,0,2) к точке (0,3,2)). Зададим контур L параметрически: x = 3cos t, y = 3sin t, z = 2 (0 ≤ t ≤ 2π). Тогда
Формула Грина.
Установим связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом по границе L этой области. Пусть в плоскости Оху дана ограниченная замкнутым контуром L правильная область D. Кривые, ограничивающие эту область снизу и сверху, заданы уравнениями y = y1(x) и y = y2(x), y1(x) ≤ y2(x), a ≤ x ≤ b (рис.1).
y=y2(x) M D N y=y1(x) Q
O a b x Рис. 1. Зададим в области D непрерывные функции P(x, y) и Q(x, y), имеющие непрерывные частные производные, и рассмотрим интеграл
Переходя к двукратному интегралу, получим:
Так как у = у2(х) – параметрическое выражение кривой МPN, то
где справа стоит криволинейный интеграл по кривой MPN. Аналогично получаем, что
Подставим полученные результаты в формулу (11.5):
так как контур L представляет собой объединение кривых MPN и NQM.
Так же можно
получить, что
Вычтем из равенства (11.6) равенство (11.7):
При этом обход контура L происходит по часовой стрелке. Изменим направление обхода. Тогда предыдущее равенство примет вид:
Эта формула, задающая связь между двойным интегралом и криволинейным интегралом 2-го рода, называется формулой Грина.
Замечание 1. Если в криволинейном интеграле по замкнутому контуру не указано направление обхода, то предполагается, что он производится против часовой стрелки.
Замечание 2. Если рассматривать в плоскости Оху векторное поле {P(x,y), Q(x,y)}, то в правой части формулы (11.8) стоит его циркуляция по контуру L.
Условия независимости криволинейного интеграла 2-го рода от пути интегрирования.
Рассмотрим
криволинейный интеграл 2-го рода
Проведем две произвольные кривые MPN и MQN, лежащие в области D и соединяющие точки M и N (рис.1).
P
Предположим,
что Тогда
Билет №34. Поверхностный интеграл первого род(по площади поверхности).Приложения(масса материальной поверхности, координаты центра тяжести, моменты, площадь искривленной поверхности).
Рассмотрим незамкнутую поверхность S, ограниченную контуром L, и разобьем ее какими-либо кривыми на части S1, S2,…, Sn. Выберем в каждой части точку Mi и спроектируем эту часть на касательную плоскость к поверхности, проходящую через эту точку. Получим в проек-ции плоскую фигуру с площадью Ti. Назовем ρ наибольшее расстояние между двумя точками любой части поверхности S.
Определение 12.1. Назовем площадью S поверхности предел суммы площадей Ti при
Поверхностный интеграл первого рода.
Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S1, S2,…, Sп (при этом площадь каждой части тоже обозначим Sп). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части Si точку Mi (xi, yi, zi) и составим интегральную сумму
Определение
12.2. Если
существует конечный предел при
Замечание. Поверхностный интеграл 1-го рода обладает обычными свойствами интегралов (линейность, суммирование интегралов от данной функции по отдельным частям рассматриваемой поверхности и т.д.).
Геометрический и физический смысл поверхностного интеграла 1-го рода.
Если подынтегральная
функция f(M)
≡ 1, то из определения 12.2 следует, что
Если же считать, что f(M) задает плотность в точке М поверхности S, то масса этой поверхности равна
Приложение поверхностного интеграла 1-го рода.
(Ω – проекция S на плоскость Оху).
Билет №35. Вычисление поверхностного интеграла 1-го рода(сведение его к кратному).
Ограничимся случаем, когда поверхность S задается явным образом, то есть уравне-нием вида z = φ(x, y). При этом из определения площади поверхности следует, что
Si
=
где (xi, yi, zi) – координаты точки Mi. Cледовательно,
Подставляя это выражение в формулу (12.2), получим, что
г z
S: z=φ(x,y)
Si L
O y Δσi Ω
x Рис. 1.
При этом в правой
части получена интегральная сумма
для функции двух переменных по плоской
области, которая в пределе при
Замечание. Уточним еще раз, что в левой части формулы (12.5) стоит поверхностный интеграл, а в правой – двойной.
Билет № 36. Поверхностный интеграл второго рода. Поток векторного поля. Связь между поверхностными интегралами первого и второго рода. Поток векторного поля.
Рассмотрим
векторное поле А(М),
определенное в пространственной
области G,
ориентированную
гладкую поверхность S
Определение 13.3. Поверхностный интеграл 1-го рода
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Замечание 1. Если выбрать другую сторону поверхности, то нормаль, а, следова-тельно, и поток изменят знак.
Замечание 2. Если вектор А задает скорость течения жидкости в данной точке, то интеграл (13.1) определяет количество жидкости, протекающей в единицу времени через поверхность S в положительном направлении (отсюда общий термин «поток»). Поверхностный интеграл второго рода.
Введем определение поверхностного интеграла 2-го рода по аналогии с соответ-ствующим криволинейным интегралом. Рассмотрим гладкую двустороннюю поверхность S, заданную уравнением z = z(x, y), в каждой точке которой определена функция f(M) = f(x, y, z), и выберем какую-либо из ее сторон (или, что то же самое, определенную ориентацию). Разобьем поверхность S на части S1, S2,…, Sп, выберем в каждой части Si точку Mi(xi, yi, zi), и умножим f(Mi) на площадь Di проекции части Si на плоскость Оху. При этом будем считать, проекция части верхней по отношению к плоскости Оху стороны рассматриваемой поверхности имеет знак «+», а нижней – знак «-». Составим сумму
Определение 13.4. Если существует конечный предел суммы (13.2) при ρ→0, не зависящий от способа разбиения поверхности и выбора точек на ней, то он называет-ся поверхностным интегралом второго рода от функции f(M) по выбранной сто-роне поверхности S и обозначается
Замечание. В этой символической записи не содержится указания на то, какая сторона поверхности выбрана, поэтому это требуется оговаривать отдельно.
Подобным образом можно проектировать части поверхности на координатные плос-кости Оxz и Оyz (при условии, что уравнение поверхности можно представить в виде y = y(x, z) или x = x(y, z) ). Получим два других поверхностных интеграла 2-го рода:
Рассмотрев сумму интегралов вида (13.3) и (13.4) по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:
Поверхностный
интеграл 2-го рода представляет собой
поток векторного поля
Отметим основное свойство поверхностного интеграла 2-го рода: При
замене рассматриваемой стороны
поверхности на противоположную
поверхностный интеграл 2-го рода меняет
знак:
Вычисление поверхностного интеграла 2-го рода.
Если задать
единичный вектор выбранной нормали
к поверхности S
в виде п
= {cos
α, cos
β, cos
γ}, где
α, β, γ –
углы, образованные нормалью с осями
координат, то
Здесь D – проекция поверхности S на плоскость Оху, а выражение для dS взято из формулы (12.5). Таким образом, вычисление поверхностного интеграла 2-го рода сводится к вычислению обычного двойного интеграла по области D от функции f, в которую вместо координаты z подставлено ее выражение из уравнения поверхности S. Обобщая эти рассуждения, получим, что
где D΄ и D΄΄ - проекции поверхности S на соответствующие координатные плоскости.
Пример. Вычислить
поверхностный интеграл 2-го рода
Применим формулу
(13.7), учитывая, что выбрана нижняя
сторона поверхности и что проекцией
части конуса на плоскость Оху
является круг
Связь поверхностных интегралов первого и второго рода.
Учитывая, что проекции элемента поверхности Si на координатные плоскости имеют вид Sicosγ, Sicosβ, Sicosα, из (13.5) получим:
где векторное
поле
Пример. Рассмотрим
интеграл
Билет 37 Векторное поле.Виды. Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор.Когда исходное пространство — евклидово (конечномерное линейное пространство со скалярным произведением), понятие векторного поля становится наглядным, и тогда векторное поле интерпретируется как способ задания движений некоторой динамической системы: вектор в данной точке описывает направление и скорость движения изображающей точки по фазовой кривой.Векторное поле, заданное на евклидовом пространстве, соответствует полю направлений, где каждой точке пространства сопоставляется некоторая прямая, проходящая через данную точку.Точка пространства, в которой векторное поле равно нулю, называется особой точкой векторного поля. В этом случае направление движения не определено, и соответствующая фазовая кривая вырождается в точку.В более общем случае, когда исходное пространство является многообразием, векторное поле — это сечение касательного расслоения к данному многообразию.В физике термин векторное поле кроме общего значения, описанного выше, имеет специальное значение, в основном в отношении фундаментальных полей (см. ниже). Смысл этого употребления сводится к тому, что фундаментальные физические поля классифицируются по природе их потенциала, и один из таких типов — векторные поля (как электромагнитное или глюонное поля). Виды векторных полей
1.Векторные
поля на прямой.
Любую
вещественнозначную функцию вещественного
переменного можно интерпретировать
как одномерное векторное поле.
2.Векторные
поля на плоскости.
Если
3.Векторные поля в трёхмерном пространстве
Если
Билет№38. Формула Гаусса-Остроградского. Дивергенция векторного поля.
Формула Гаусса-Остроградского.
З z
S2 (z=f2(x,y))
S3
V S1 (z=f1(x,y))
O y
x D Рис. 1. Будем считать, что поверхность S можно разбить на три части: S1, заданную уравнением z = f1(x, y), S2 ( z = f2 (x, y) ) и S3 – цилиндрическую поверхность с образующей, параллель-ной оси Oz (рис.1). Зададим в каждой точке области V и поверхности S непрерывные функции P(x, y, z), Q(x, y, z) и R(x, y, z) и вычислим интеграл
Зададим ориентацию поверхности S, выбрав направление внешней нормали, тогда на S1 cos(n, z) < 0, на S2 cos(n, z) > 0, a на S3 cos(n, z) = 0. Двойные интегралы, стоящие в правой части предыдущего равенства, равны соответствующим поверхностным интегралам:
(Знак «-» во втором интеграле появляется за счет того, элементы площади поверхности S1 и области D связаны соотношением dxdy = ΔS(-cos(n, z)) ). Следовательно, исходный интеграл можно представить в виде:
Окончательный результат можно записать так:
Таким же образом можно получить соотношения
Складывая эти три равенства, получаем формулу Гаусса-Остроградского:
Воспользовавшись формулой 13.9, задающей связь между поверхностными интегралами 1-го и 2-го рода, можно записать формулу Гаусса-Остроградского в ином виде:
где запись «S+» означает, что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.
Дивергенция векторного поля.
Продолжим изучение характеристик векторных полей.
Определение 15.1. Дивергенцией векторного поля A = {Ax, Ay, Az}, где Ax, Ay, Az – функции от x, y, z, называется
Замечание 1. Из определения видно, что дивергенция является скалярной функцией. Замечание 2. Слово «дивергенция» означает «расходимость», так как дивергенция харак-теризует плотность источников данного векторного поля в рассматриваемой точке.
Рассмотрим формулу Гаусса-Остроградского с учетом определений потока и дивергенции векторного поля. Тогда в левой части формулы (15.1) стоит тройной интеграл по объему V от дивергенции векторного поля {P, Q, R}, а в правой – поток этого вектора через ограни-чивающую тело поверхность S:
Докажем, что величина дивергенции в данной точке не зависит от выбора системы коор-динат. Рассмотрим некоторую точку М, которую окружает трехмерная область V, ограни-ченная поверхностью S. Разделим обе части формулы (15.4) на V и перейдем к пределу при стягивании тела V к точке М. Получим:
Это равенство можно считать инвариантным определением дивергенции, то есть определением, не зависящим от выбора координатной системы.
Билет№39. Формула Стокса. Ротор векторного поля.
Формула Стокса.
Рассмотрим поверхность S такую, что любая прямая, параллельная оси Оz, пересекает ее в одной точке. Обозначим границу поверхности λ и выберем в качестве положительного направления нормали такое, при котором она образует с положительным направлением оси Оz острый угол. Если уравнение поверхности имеет вид z = f(x, y), то направляющие косинусы нормали задаются формулами
Рассмотрим некоторую трехмерную область V, в которой целиком лежит поверхность S, и зададим в этой области функцию P(x, y, z), непрерывную вместе с частными производны-ми первого порядка. Вычислим криволинейный интеграл 2-го рода по кривой λ: λ
O y x L
Рис. 2. Уравнение линии λ имеет вид z = f(x, y), где х, у – координаты точек линии L, являющейся проекцией λ на плоскость Оху (рис.2). Поэтому, используя формулу (10.8), получаем:
Обозначим P(x, y) = P(x, y, f(x, y)), Q(x, y) = 0 и применим к интегралу, стоящему в правой части предыдущего равенства, формулу Грина:
где область D ограничена линией L. Преобразуем левое подынтегральное выражение, используя формулу производной сложной функции:
и подставим его в предыдущее равенство:
так
как
При этом направление обхода контура λ выбирается соответствующим положительному направлению нормали (рис.2). Задавая в области V непрерывно дифференцируемые функции Q(x, y, z) и R(x, y, z), можно получить для них аналогичные соотношения:
Складывая левые и правые части полученных равенств, получим формулу Стокса, уста-навливающую связь между поверхностным интегралом 1-го рода по поверхности σ и криволинейным интегралом 2-го рода по ограничивающему ее контуру λ с учетом ориен-тации поверхности:
Последняя запись позволяет лучше запомнить подынтегральное выражение в правой части формулы Стокса, которое можно получить, раскрывая определитель по первой строке и учитывая, что во второй его строке стоят операторы частного дифференцирова-ния по соответствующим переменным, применяемые к функциям, стоящим в третьей строке. Используя связь между поверхностными интегралами 1-го и 2-го рода (формула (13.9)), можно записать формулу Стокса в ином виде:
Ротор векторного поля.
Определение 15.2. Ротором или вектором вихря векторного поля A = {Ax, Ay, Az}, где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
Замечание 1. Ротор характеризует завихренность поля А в данной точке, то есть наличие вращательных движений, так как его модуль равен удвоенной угловой скорости в этой точке.
Замечание 2. Формула Стокса в векторной формулировке имеет вид:
то есть циркуляция вектора по замкнутому контуру равна потоку ротора этого вектора через поверхность, натянутую на данный контур.
Замечание 3. Можно дать другое, инвариантное, определение ротора. Для этого рассмотрим произвольное направление п, исходящее из данной точки М, и окружим эту точку плоской площадкой σ, перпендикулярной к п и ограниченной контуром λ. Приме-няя формулу Стокса, получим:
Разделив обе части этого равенства на σ и стягивая площадку σ к данной точке, найдем в пределе, что
Тем самым можно определить проекцию ротора на любую ось, то есть вектор rot A не зависит от выбора координатной системы.
Билет №40. Сумма ряда. Сходимость. Ряд, составленный из членов бесконечно убывающей геометрической прогрессии. Основные свойства числовых рядов. Необходимый признак сходимости. Гармонический ряд.
Определение
Если дана
бесконечная последовательность чисел
называется
числовым
рядом;
числа
Если дан ряд (1),
то сумма первых n
членов этого ряда называется
– ……………………….
... – ………………………. образуют
последовательность частичных сумм
Определение
Ряд (1) называется
сходящимся,
если существует конечный предел
последовательности частичных сумм,
то есть
3 ОСНОВНЫЕ СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
также сходится,
и его сумма равна
Эти свойства доказываются с помощью определения сходящихся рядов. Для примера докажем второе свойство.
Пусть
Очевидно, что
при любом
На практике часто не столь важно найти сумму ряда, как ответить на вопрос о сходимости ряда. Для этой цели используются признаки сходимости, основанные на свойствах общего члена ряда. НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА ТЕОРЕМА 1
Если ряд
Кратко: если ряд сходится, то его общий член стремится к нулю.
Доказательство.
Пусть ряд сходится и его сумма равна
Тогда
Из доказанного
необходимого признака сходимости
вытекает достаточный
признак расходимости ряда:
если при
|


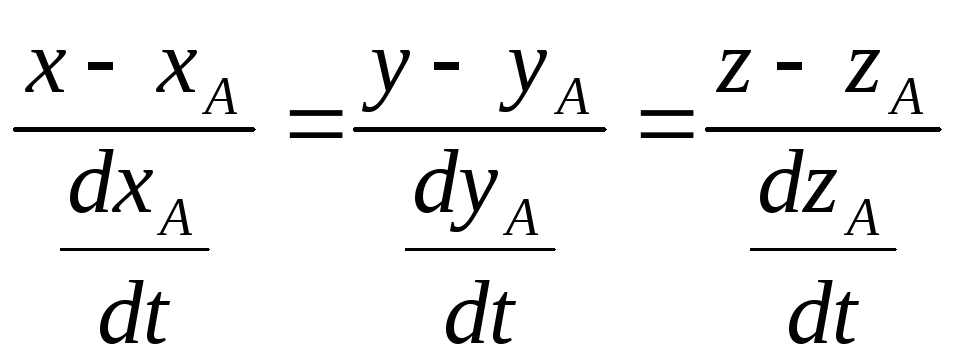 .
.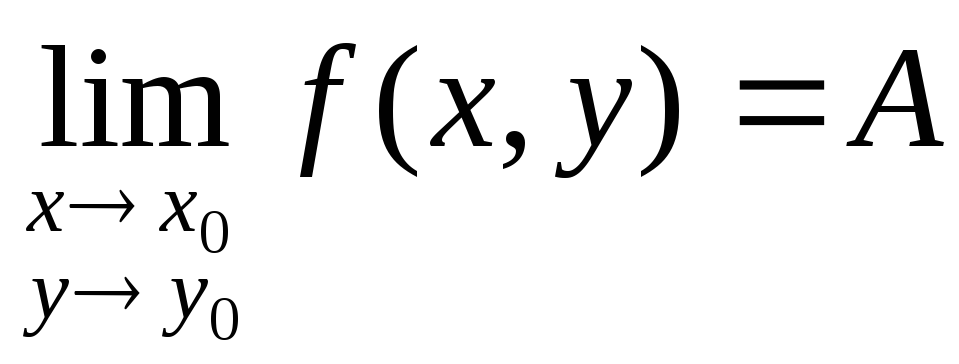
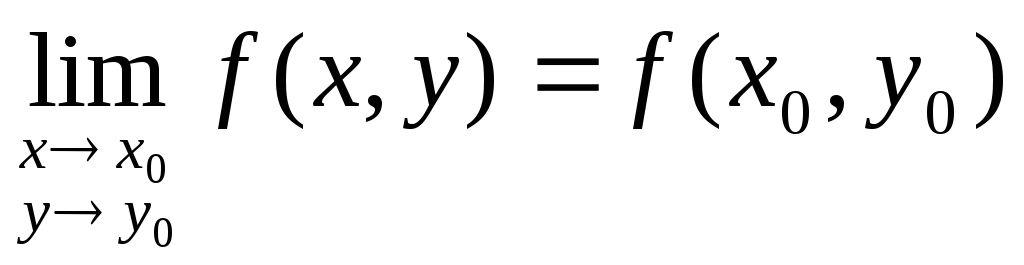 (1)
(1)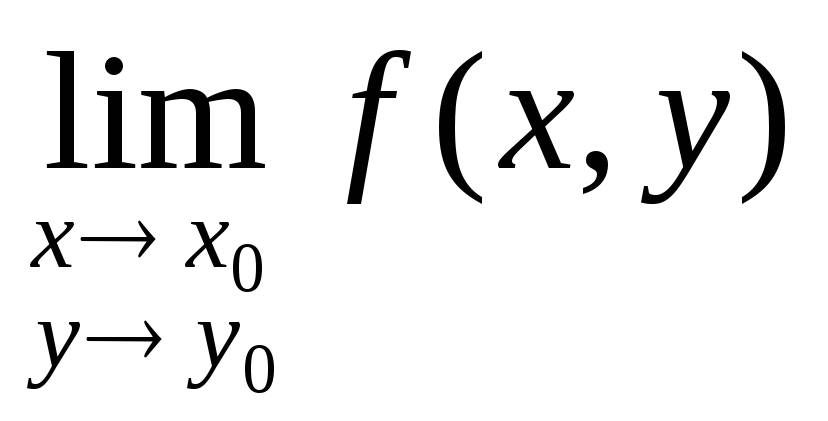 .
. пр.:
Приращением функции
пр.:
Приращением функции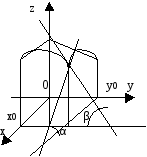 еометрический
смысл: Частная производная равна
тангенсу угла наклона касательной,
проведенной к функции с плоскостью
еометрический
смысл: Частная производная равна
тангенсу угла наклона касательной,
проведенной к функции с плоскостью
 нормаль
нормаль


 M
M
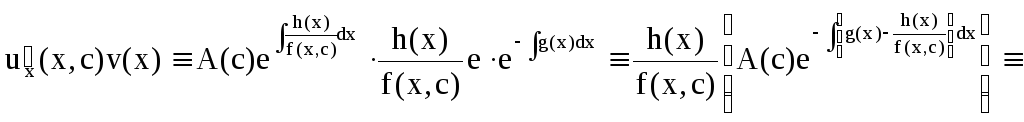
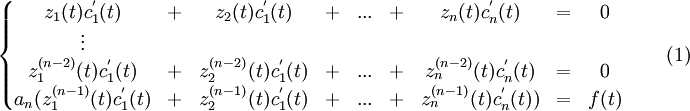

 Тогда общее
решение запишется
Тогда общее
решение запишется
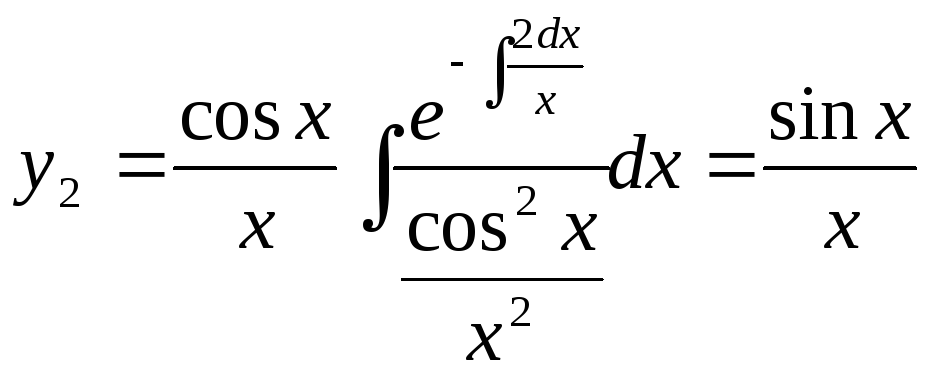
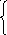
 огда
имеем систему (5). Умножим уравнение
(5)на единицу, Р1(х) и Р2(х) начиная снизу
и сложим:
огда
имеем систему (5). Умножим уравнение
(5)на единицу, Р1(х) и Р2(х) начиная снизу
и сложим: .
.

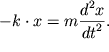
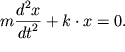
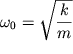 (частота
собственных незатухающих колебаний
или собственная
частота),
окончательно получим
(частота
собственных незатухающих колебаний
или собственная
частота),
окончательно получим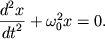
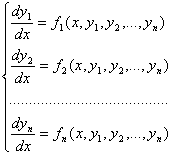 (1)
(1)
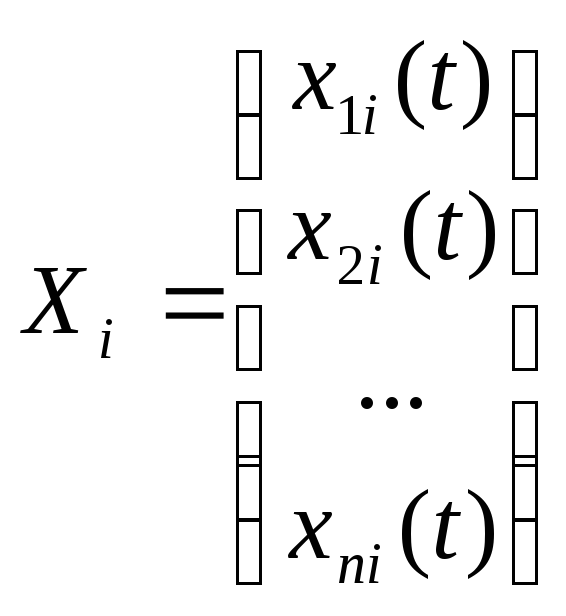 ,
называются линейно
зависимыми при
,
называются линейно
зависимыми при
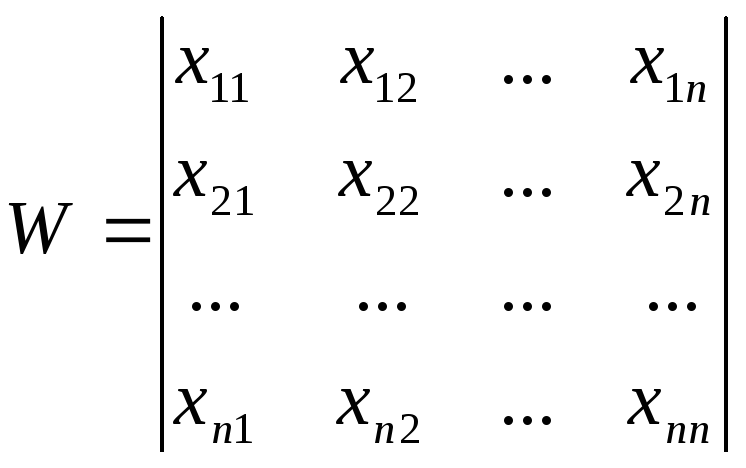 ,
(5)
,
(5)
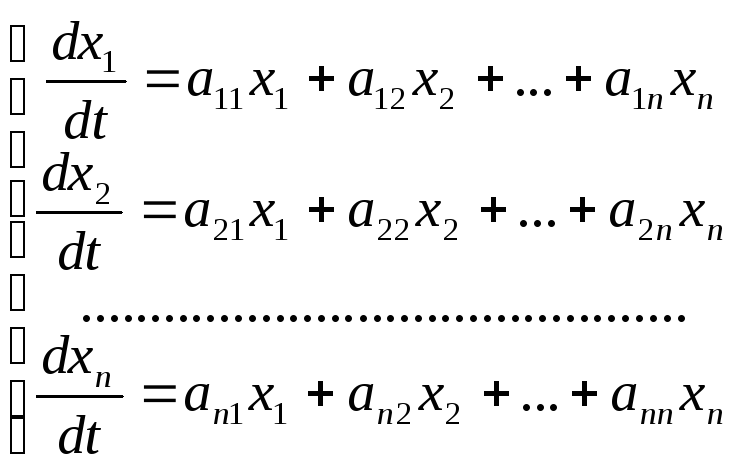 (23.6)
(23.6)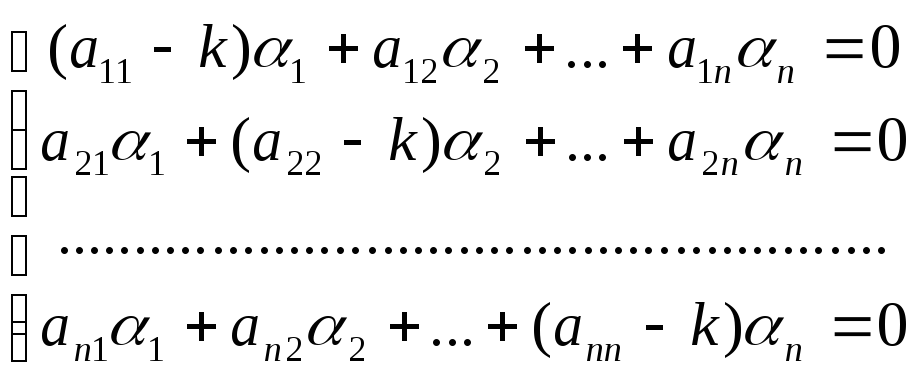 .
(23.8)
.
(23.8)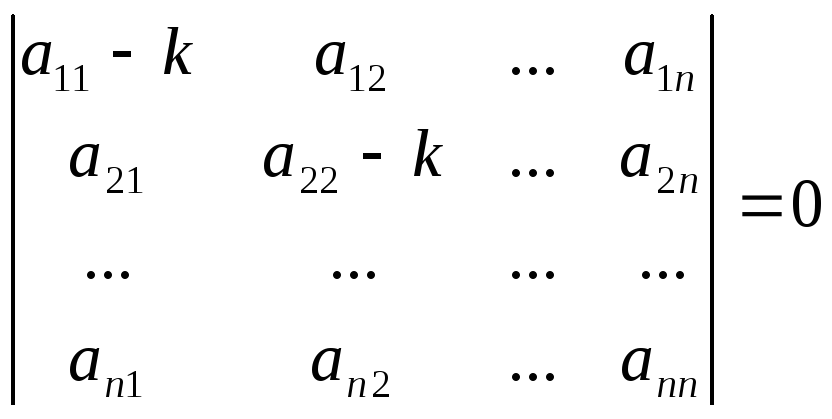 ,
(23.9)
,
(23.9)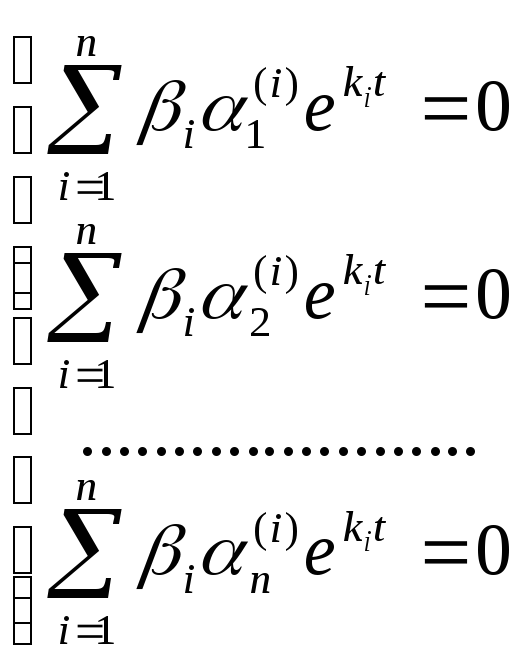 (*)
(*)
 (**) , то в силу линейной независимости
функций
(**) , то в силу линейной независимости
функций
 ассмотрим
в плоскости Оху
замкнутую область D,
ограниченную линией L.
Разобьем эту область какими-нибудь
линиями на п
частей
ассмотрим
в плоскости Оху
замкнутую область D,
ограниченную линией L.
Разобьем эту область какими-нибудь
линиями на п
частей
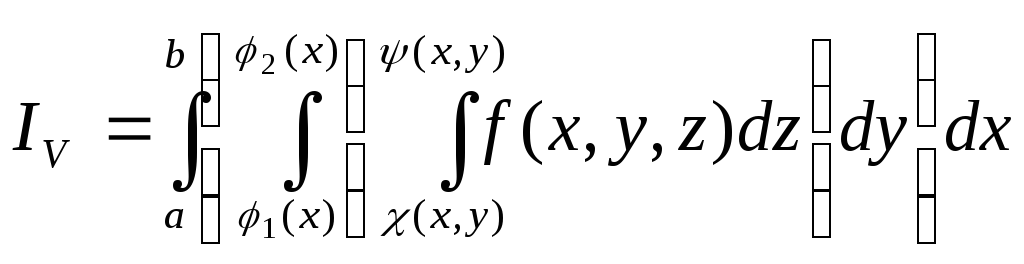 .
(9.1)
.
(9.1)
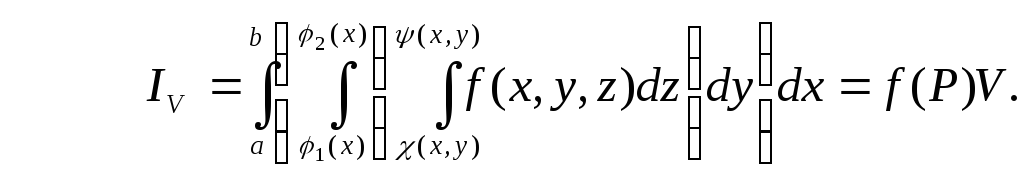
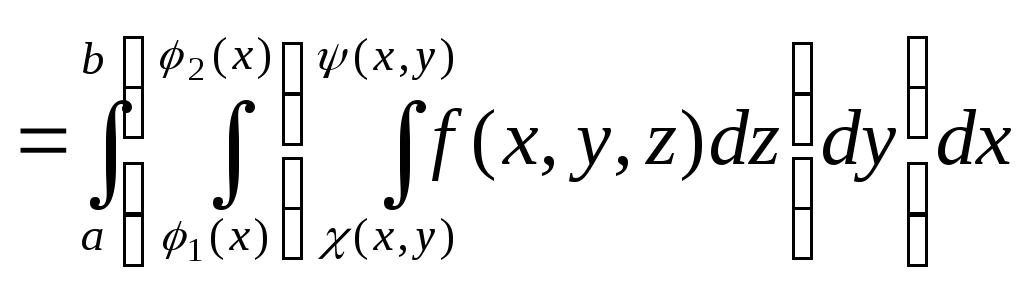 .
(9.3)
.
(9.3)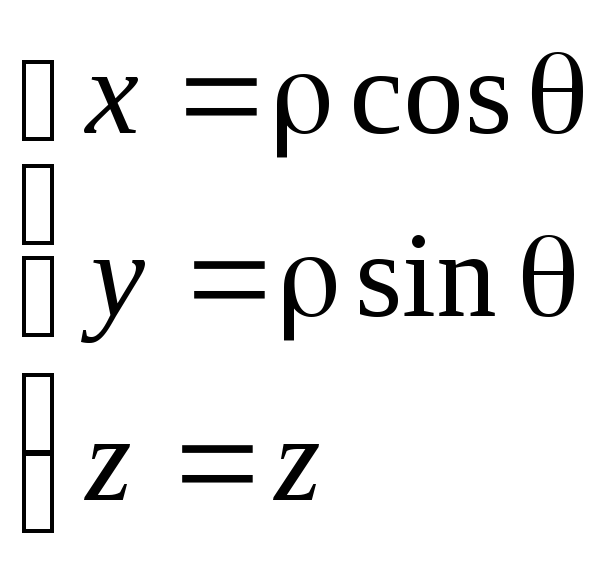
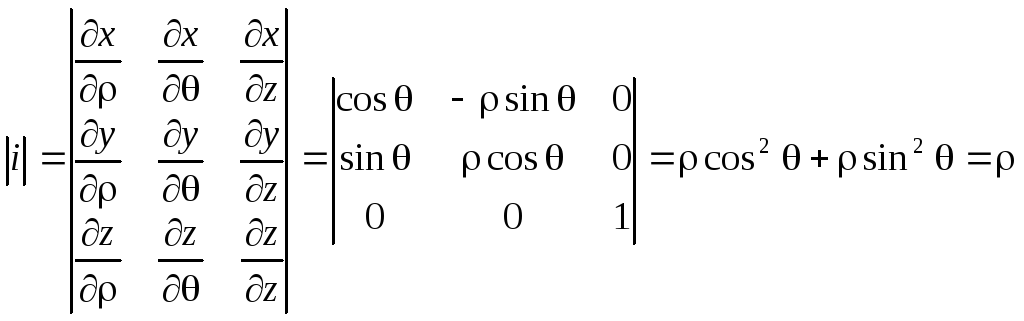

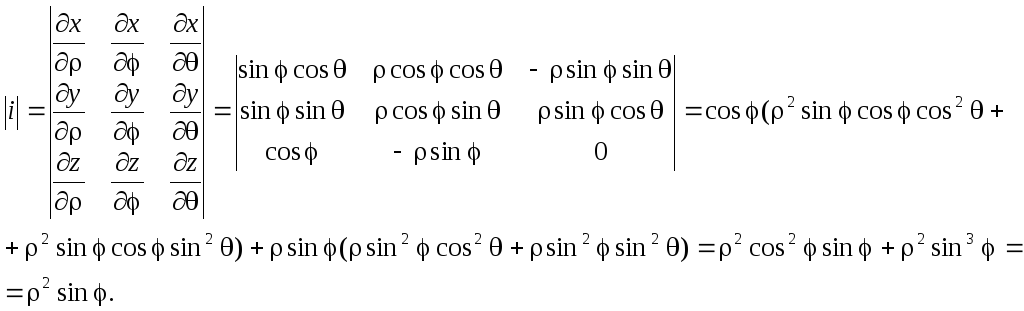
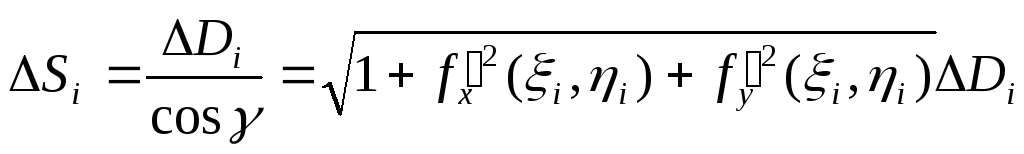

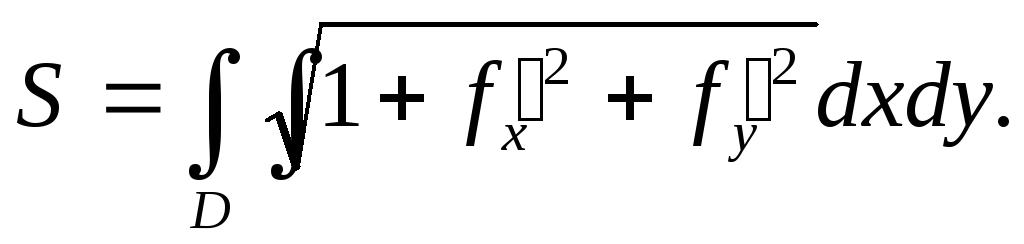
 у
у


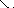

 ηi
Pi
ηi
Pi
 O
ξi
x
O
ξi
x
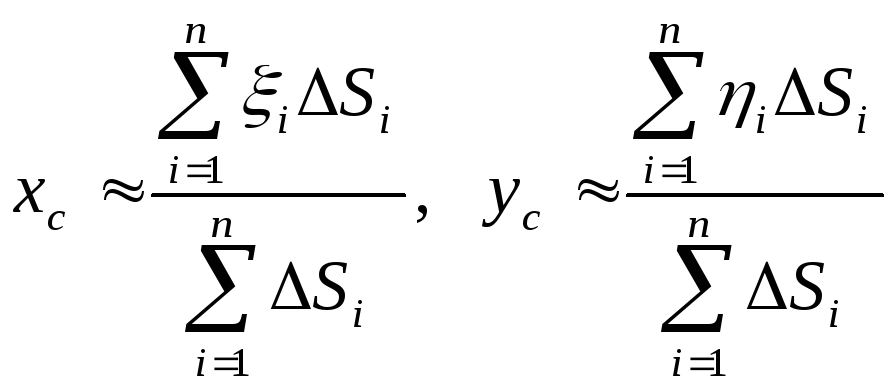 .
.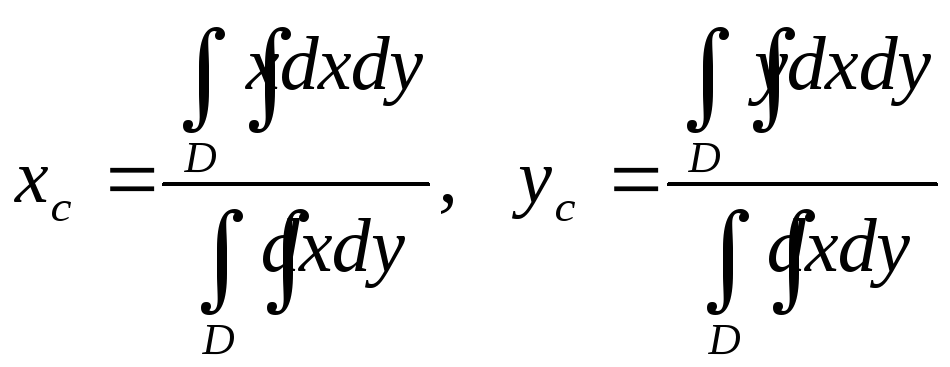 .
(5)
.
(5) .
.
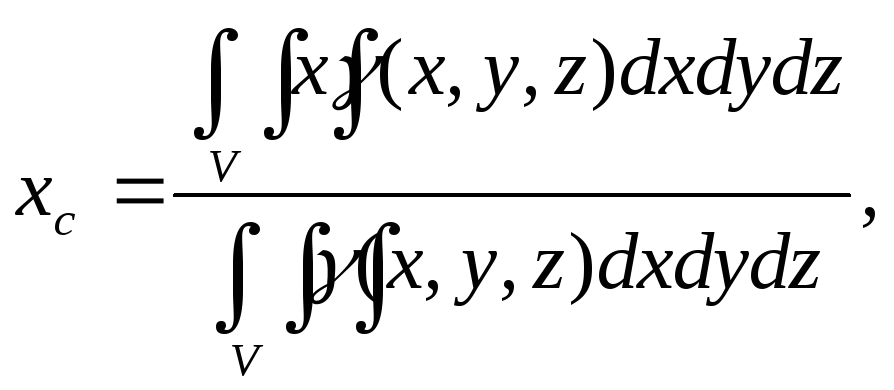
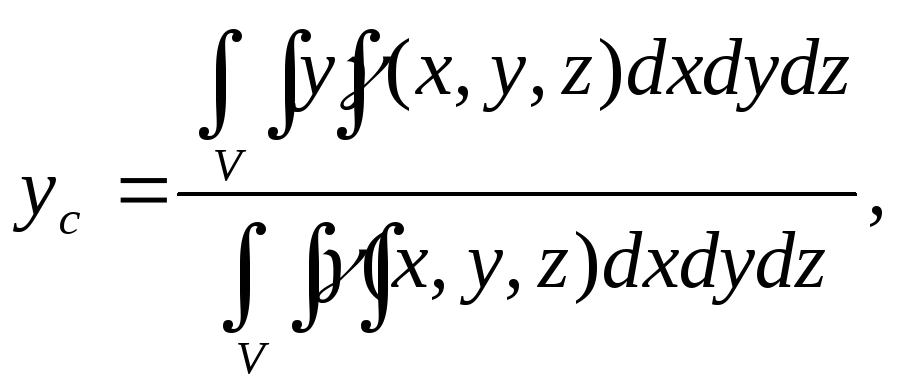
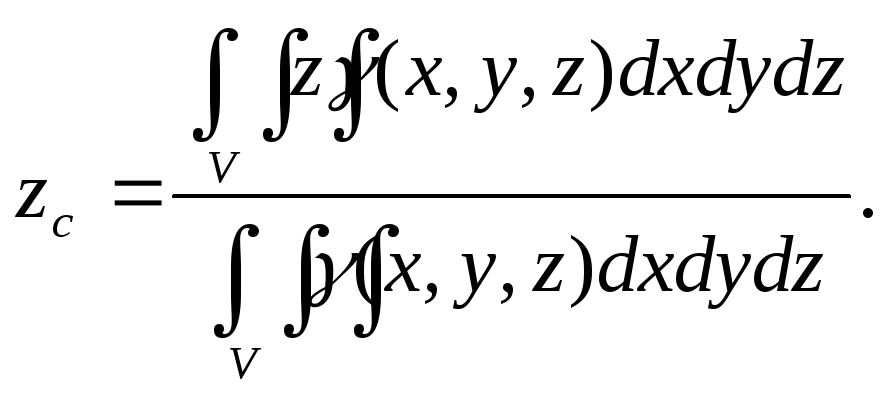 (7)
(7)
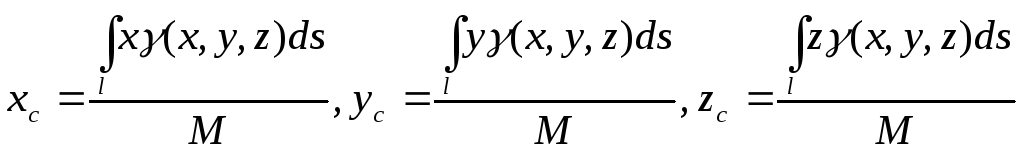 .
(14.19)
.
(14.19)
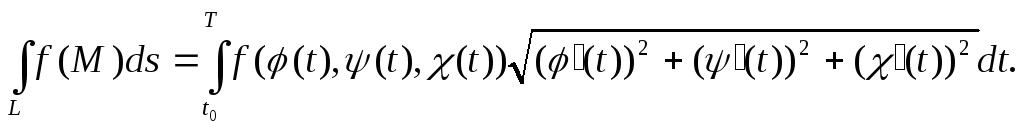 (10.4)
(10.4) y
y





 P
P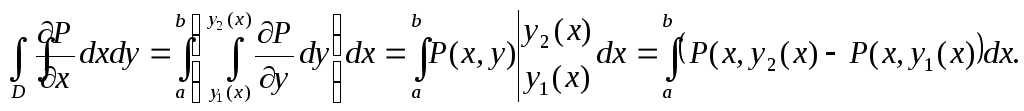 (11.5)
(11.5)
 Q
Q
 • М
• N
Рис.
1.
• М
• N
Рис.
1.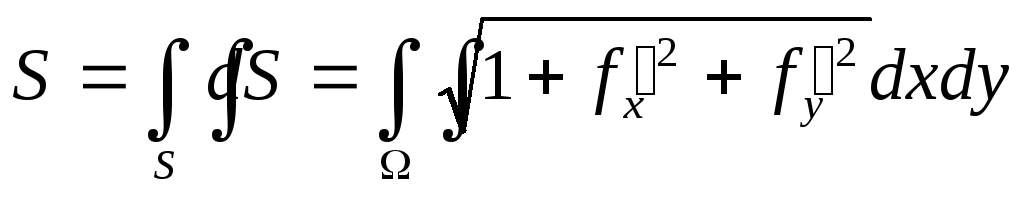 (14.21)
(14.21)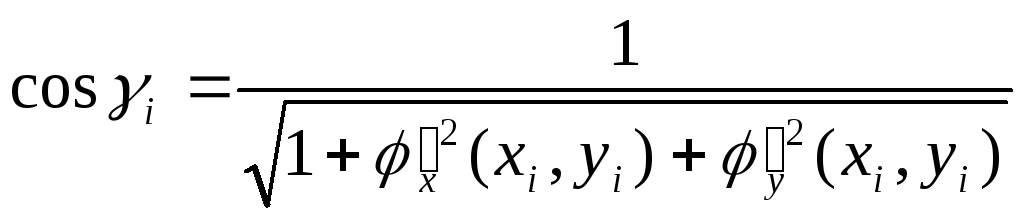 ,
, .
.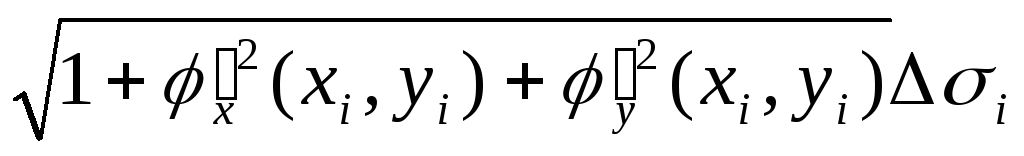 ,
,









 де
суммирование справа проводится по
области Ω плоскости Оху,
являющейся проекцией на эту плоскость
поверхности S
(рис.1).
де
суммирование справа проводится по
области Ω плоскости Оху,
являющейся проекцией на эту плоскость
поверхности S
(рис.1). (выбор знака зависит от направления
нормали). Тогда из (13.2), (13.3) следует,
что
(выбор знака зависит от направления
нормали). Тогда из (13.2), (13.3) следует,
что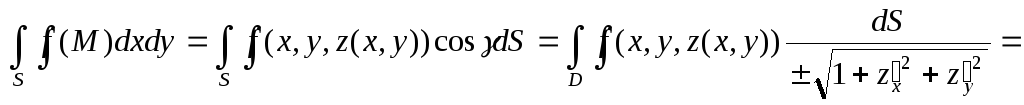
 .
(13.7)
.
(13.7)







 ададим
в пространстве замкнутую трехмерную
область V,
ограниченную поверхностью
S
и
проектирующуюся на плоскость Оху
в правильную
область D.
ададим
в пространстве замкнутую трехмерную
область V,
ограниченную поверхностью
S
и
проектирующуюся на плоскость Оху
в правильную
область D.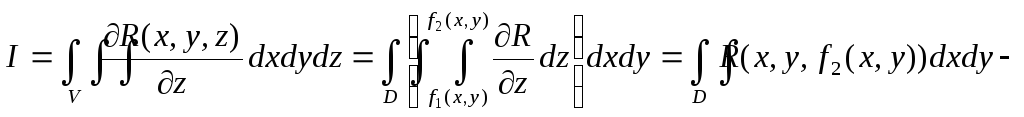
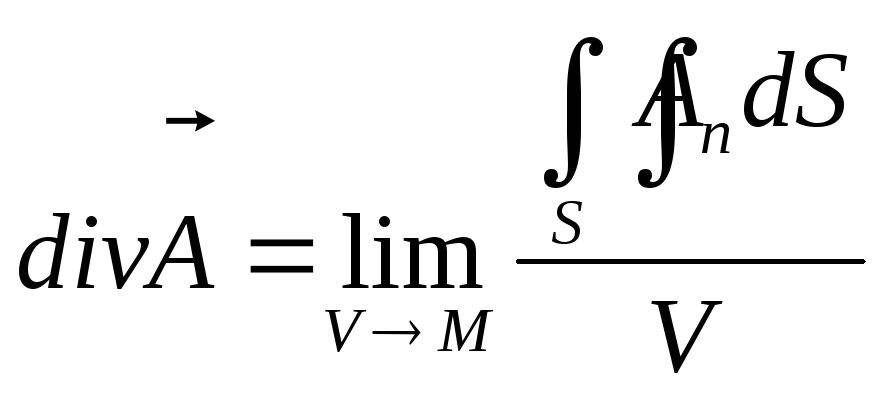 .
(15.5)
.
(15.5)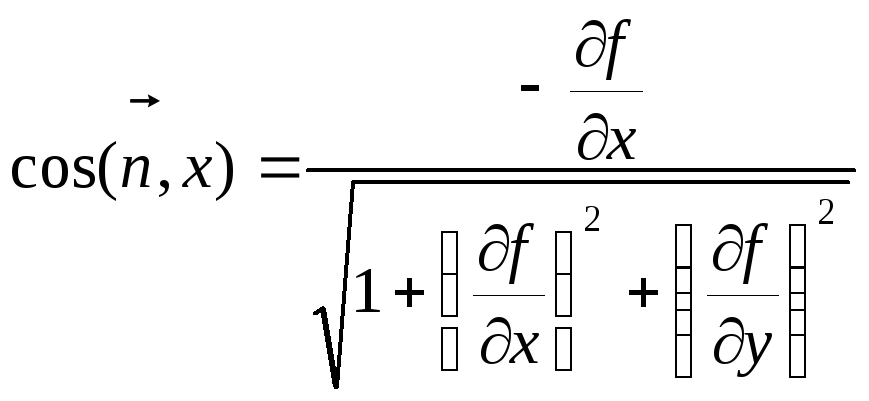 ,
,
 ,
,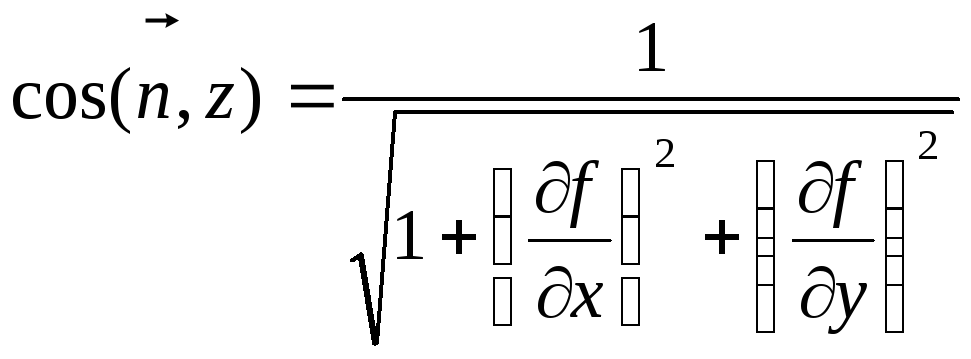 .
.
 z
z
 n
n








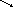 σ
σ
 D
D
 (15.6)
(15.6)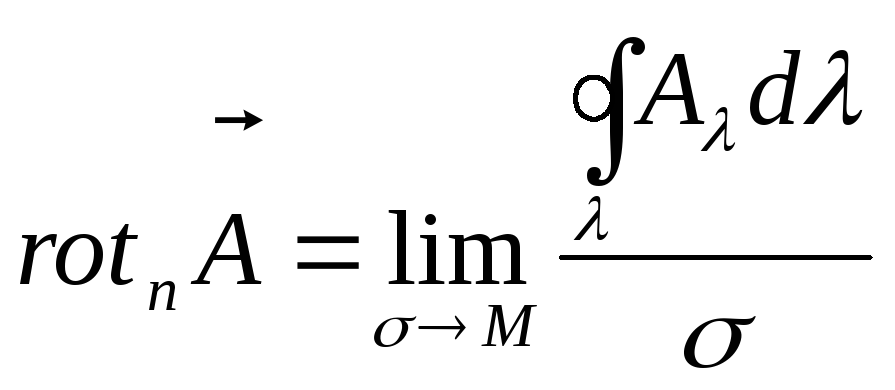 .
.