Результат

корень x=4.5768

значение функции y=0.000

количество приближений k= 49

y

*

yl

* yr

| | | |

y a xl xr b

*

yl * yr

| | | | |

a xl xr b

Рис. 2.3 Предыдущее и последующее приближения метода

золотого сечения

a, b, f(x)

g=0.618034

xl=b-(b-a)g, yl=f²(xl)

xr=a+(b-a)g, yr=f²(xr)

k=0

k=k+1

нет yl< yr да

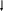
a=xl, xl=xr, yl=yr b=xr, xr=xl, yr=yl

xr=a+(b-a)g, yr=f²(xr) xl=b-(b-a)g, yl=f²(xl)

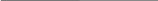
нет |b-a|

да

x=(a+b)/2

x, y=f²(x)

Рис. 2.4 Блок-схема алгоритма метода золотого сечения

Рабочее задание

С использованием ЭВМ отделить один из действительных корней.Со- ставить программу метода половинного деления и с точностью =0.0001 найти один действительный корень. Для четных вариантов составить программу метода золотого сечения, а для нечетных - метода дробления шага, и с точностью =0.0001 найти один действительный корень.

Написать отчет, содержащий:

- задание;

- принятые обозначения;

- программы отделения корней, метода половинного деления и золотого

сечения или дробления шага;

- результаты.

Варианты заданий к лабораторной работе 2

Таблица 2.1

№ вари анта	Уравнение
1	x3+2x2+2=0
2	x3-3x2+9x-10=0
3	x3-2x+2=0
4	x3+3x-1=0
5	x3+x-3=0
6	x3+0.4x2+0.6x-1.6=0
7	x3-0.2x2+0.4x-1.4=0
8	x3-0.1x2+0.4x+2=0
9	x3+3x2+12x+3=0
10	x3-0.2x2+0.5x-1=0
11	x3-0.1x2+0.4x+1.2=0
12	x3-3x2+6x-5=0
13	x3-0.2x2+0.5x-1.4=0
14	x3+2x+4=0
15	x3-3x2+12x-12=0
16	x3+0.2x2+0.6x+0.8=0
17	x3+4x-6=0
18	x3+0.1x2+0.4x-1.2=0
19	x3+3x2+6x-1=0
20	x3-0.1x2+0.4x-1.5=0

Лабораторная работа 3

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

ПРЯМЫМИ МЕТОДАМИ

Методы решения систем линейных уравнений делятся на две группы: прямые (точные) и итерационные.

Прямые методы дают решение после заранее известного количества операций. Эти методы сравнительно просты и универсальны, но требуют относительно много места в памяти ЭВМ. Кроме того, им свойственно накапливание погрешностей в процессе решения, поскольку вычисления на любом этапе используют результаты предыдущих операций. Вслед-ствие этого прямые методы применяют обычно для решения сравни-тельно небольших (n<200) систем. К прямым методам относятся метод Гаусса и его многочисленные модификации.

В итерационных методах решение получается как предел после- довательных приближений, вычисляемых некоторым единообразным процессом. Для итерационных методов существенной характеристикой оказывается быстрота сходимости. В этом смысле итерационные мето-ды не являются универсальными: давая быструю сходимость для одних систем уравнений, они могут медленно сходиться или даже вовсе не сходиться для других. В сравнении с прямыми итерационные методы требуют несколько меньшего объема памяти. Погрешности окончатель-ных результатов не накапливаются, поскольку точность вычислений в каждой итерации определяется лишь результатами предыдущей итера-ции и практически не зависит от ранее выполненных вычислений. Все это оказывается особенно ощутимым при решении больших систем урав-нений. К итерационным методам относятся метод простой итерации и метод Зейделя.

Систему уравнений будем записывать в виде:

a_{1 1}x₁+a_{1 2}x₂+ . . . +a_{1 n}x_n=a_{1 n+1} ,

a_{2 1}x₁+a_{2 2}x₂+ . . . +a_{2 n}x_n=a_{2 n+1} , (3.1)

. . . . . . . . . .

a_{n 1}x₁+a_{n 2}x₂+ . . . +a_{n n}x_n=a_{n n+1} ,

позволяющем несколько упростить тексты программ. В матричной форме левую часть этой системы можно представить как произведение квад-ратной матрицы коэффициентов ( матрицы системы) на вектор-столбец неизвестных. В правой части размещается вектор-столбец свободных членов:

a_{1 1} a_{1 2} . . . a_{1 n} x₁ a_{1 n+1}

a_{2 1} a_{2 2} . . . a_{2 n} x₂ a_{2 n+1} (3.2)

. . . . * =

a_{n 1} a_{n 2} . . . a_{n n} x_n a_{n n+1}

или

a_{i k}x_k=a_{i n+1} i=1, 2, ...n (3.3)