ВВЕДЕНИЕ
Методические указания к выполнению лабораторных работ по мето-дам вычислений имеют своей целью ознакомить с наиболее употреби-тельными численными методами и привить навыки выполнения расчетов на ЭВМ при решении инженерных задач. При составлении заданий использовались тексты лабораторных работ, разработанных препода-вателями кафедры.
Лабораторная работа 1
ВЫЧИСЛЕНИЕ ФУНКЦИЙ
Для вычисления функций с помощью арифметических операций (сло-жение, вычитание, умножение, деление) может использоваться разложе-ние в степенные ряды по формуле Маклорена:
.
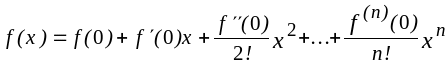
Например, функции еx, sin x, cos x разлагаются в следующие степен-ные ряды:
,
,
,
сходящиеся при любом значении x.
Разложение в ряд логарифмической функции
сходится при 0<x<2.
Для возведения в дробные степени и извлечения корней удобнее использовать формулу бинома Ньютона:
Если коэффициенты степенного многочлена (полинома) уже вычислены и полином представляется в виде:
y=a0+a1x+a2x2+...+anxn ,
то для вычисления его значения наиболее рациональной является, так называемая, схема Горнера
y=a0+x(a1+x(a2+...+x(an-1+anx)...)) .
Фрагмент программы на языке Паскаль в этом случае записывается в следующем виде:
y:= a[ n ];
for i:= n-1 downto 0 do
y:= y*x+a[ i ];
В ряде случаев при вычислении значений сумм степенных рядов возможно использование рекуррентных соотношений, которые позво-ляют вычислять очередной член ряда не непосредственно, а через уже вычисленные предыдущие члены. Для нахождения рекуррентного соотношения можно взять отношение двух соседних членов.
Например, для функции sin x модуль общего члена ряда имеет вид
.
.
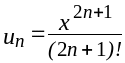Взяв отношение последующего члена к предыдущему, получим
.
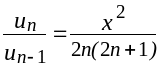Таким образом, для двух соседних членов ряда получаем рекуррентное соотношение
.
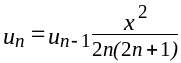Пример расчета функции суммированием ряда
Пример вычисления sin x с точностью до =10-6 с использованием рекуррентного соотношения.
Текст программы
program prsin;
var x,y,z,u,eps:real; n:integer;
begin eps:=1e-6;
writeln('введите аргумент x=');
read(x);
y:=x; u:=x; n:=1; z:=-1;
repeat u:=u*x*x/(2*n)/(2*n+1);
y:=y+z*u;
n:=n+1;
z:=-z;
until u<=eps;
writeln('x=',x:8:5,' y=',y:8:5,' n=',n);
writeln('sin x=',sin(x):8:5)
end.
Рабочее задание
Разложить функцию, заданную в табл. 1.1., в степенной ряд.
Составить программу, рассчитать значение функции суммированием членов ряда с точностью =10-6 и количество членов ряда n.
Составить программу и рассчитать коэффициенты степенного ряда a0, a1,...an для n членов ряда.
Составить программу и рассчитать значение функции суммированием n членов ряда по схеме Горнера.
Рассчитать значение функции с использованием стандартных функций языка.
Написать отчет, содержащий:
- рабочее задание;
- тексты программ расчета функции прямым суммированием членов ряда, расчета коэффициентов ряда и расчета функции по схеме Горнера;
- результаты расчетов.
Варианты заданий к лабораторной работе 1
Таблица 1.1
-
№
вари-
анта
Функция y=f(x)
Аргумент x
и
параметр a
1
y=sh x=(ex-e-x)/2
x=0.95
2
y=ch x=(ex+e-x)/2
x=0.93
3
y=ln(1+x)
x=0.91
4
y=ln(1-x)
x=0.89
5
y=ln(a+x)
x=0.15 a=0.65
6
y=ln(a-x)
x=0.15 a=0.65
7
y=ax
x=0.15 a=0.65
8
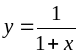
x=0.87
9
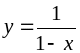
x=0.85
10
x=0.83
11
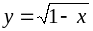
x=0.81
12
x=0.79
13
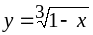
x=0.77
14
y=arc sin x
x=0.75
15
y=arc cos x
x=0.73
16
y=arc tg x
x=0.71
Лабораторная работа 2
РЕШЕНИЕ УРАВНЕНИЙ С ОДНОЙ НЕИЗВЕСТНОЙ
Обычная запись уравнения с одной неизвестной:
f(x)=0 , (2.1)
где f(x) - непрерывная функция.
Всякое значение x, при котором f(x) превращается в нуль, называ-ется корнем уравнения, а процесс нахождения корней - решением урав-нения.
Задачей численного решения является определение приближенного значения корня или установление отрезка [a,b], содержащего значение корня, с требуемой точностью. Численное решение обычно выполняется в два этапа: отделение корней и уточнение корней уравнения. На первом этапе довольно грубо определяются границы отрезка [a,b], содержащего корень, а на втором этапе производится уточнение значения корня или сближение границ отрезка [a,b] до заданной степени точности.