
- •Наивная теория множеств
- •Аксиоматическая теория множеств
- •Аксиомы Пеано
- •Теоретико-множественное определение (Определение Фреге-Рассела)
- •0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (Последовательность a000045 вOeis)
- •1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (Последовательность a001175 в oeis)
- •Обозначения
- •Основные свойства
- •Математическая модель
- •Доказательство
- •Свойства нок
- •Свойства нод
Аксиомы Пеано
Множество
будем
называть множеством натуральных чисел,
если зафиксирован некоторый
элемент ![]() (единица)
и функция
(единица)
и функция ![]() (функция
следования) так, что выполнены следующие
условия
(функция
следования) так, что выполнены следующие
условия
(1 является натуральным числом);
Если
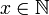 ,
то
,
то 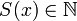 (Число,
следующее за натуральным, также является
натуральным);
(Число,
следующее за натуральным, также является
натуральным);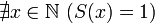 (1 не
следует ни за каким натуральным числом);
(1 не
следует ни за каким натуральным числом);Если S(b) = a и S(c) = a, тогда b = c (если натуральное число a непосредственно следует как за числом b, так и за числом c, то b= c);
Аксиома индукции. Пусть P(n) — некоторый одноместный предикат, зависящий от параметра — натурального числа n. Тогда:
если P(1) и ![]() ,
то
,
то ![]()
(Если некоторое высказывание P верно для n = 1 (база индукции) и для любого n при допущении, что верно P(n), верно и P(n+ 1) (индукционное предположение), то P(n) верно для любых натуральных n).
Перечисленные аксиомы отражают наше интуитивные представления о «натуральном ряде».
Принципиальным фактом
является то, что эти аксиомы по сути
однозначно определяют натуральные
числа (категоричность системы аксиом
Пеано). А именно, можно доказать (см.[1],
а также краткое доказательство[2]),
что если ![]() и
и ![]() —
две модели для системы аксиом Пеано, то
они необходимо изоморфны, то есть
существует биекция
—
две модели для системы аксиом Пеано, то
они необходимо изоморфны, то есть
существует биекция ![]() такая,
что
такая,
что ![]() и
и ![]() для
всех
.
для
всех
.
Поэтому, достаточно зафиксировать в качестве какую-либо одну конкретную модель множества натуральных чисел, например, ту, что описана ниже.
Теоретико-множественное определение (Определение Фреге-Рассела)
Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
Ноль как натуральное число
Иногда, в иностранной и переводной литературе, в первой и третьей аксиомах Пеано заменяют 1 на 0. В этом случае ноль считается натуральным числом. При определении через классы равномощных множеств 0 является натуральным числом по определению. Специально отбрасывать его было бы неестественно. Кроме того, это значительно усложнило бы дальнейшее построение и применение теории, так как в большинстве конструкций ноль, как и пустое множество, не является чем-то выделенным. Одним из преимуществ натурального нуля является то, что при этом образует полугруппу с единицей.
В русской литературе
обычно ноль исключён из числа натуральных
чисел ![]() ,
а множество натуральных чисел с нулём
обозначается как
,
а множество натуральных чисел с нулём
обозначается как ![]() .
Если в определение натуральных чисел
включен ноль, то множество натуральных
чисел записывается как
,
а без нуля как
.
Если в определение натуральных чисел
включен ноль, то множество натуральных
чисел записывается как
,
а без нуля как ![]() .
.
В международной
математической литературе, с учётом
сказанного выше и во избежание
неоднозначностей, множество ![]() обычно
называют множеством положительных
целых чисел и обозначают
обычно
называют множеством положительных
целых чисел и обозначают ![]() .
Множество
.
Множество ![]() зачастую
называют множеством неотрицательных
целых чисел и обозначают
зачастую
называют множеством неотрицательных
целых чисел и обозначают ![]() .
.
Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Сложение. Слагаемое + Слагаемое = Сумма
Умножение. Множитель * Множитель = Произведение
Возведение в степень ab, где a — основание степени и b — показатель степени. Если основание и показатель натуральны, то и результат будет являться натуральным числом.
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
Вычитание. Уменьшаемое − Вычитаемое = Разность. При этом Уменьшаемое должно быть больше Вычитаемого (или равно ему, если считать 0 натуральным числом).
Деление. Делимое / Делитель = (Частное, Остаток). Частное p и остаток r от деления a на b определяются так: a = p * b + r, причём
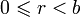 .
Заметим, что именно последнее условие
запрещает деление на ноль, так как
иначе a можно представить в
виде a = p * 0 + a,
то есть можно было бы считать частным 0,
а остатком = a.
.
Заметим, что именно последнее условие
запрещает деление на ноль, так как
иначе a можно представить в
виде a = p * 0 + a,
то есть можно было бы считать частным 0,
а остатком = a.
Следует заметить, что именно операции сложения и умножения являются основополагающими. В частности, кольцо целых чиселопределяется именно через бинарные операции сложения и умножения.
Теоретико-множественные определения
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Будем обозначать класс эквивалентности множества A относительно биекций как [A]. Тогда основные арифметические операции определяются следующим образом:
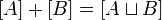

[A][B] = [AB]
где ![]() — дизъюнктное
объединение множеств,
— дизъюнктное
объединение множеств, ![]() — прямое
произведение, AB —
множество отображений из B в A.
Можно показать, что полученные операции
на классах введены корректно, то есть
не зависят от выбора элементов классов,
и совпадают с индуктивными определениями.
— прямое
произведение, AB —
множество отображений из B в A.
Можно показать, что полученные операции
на классах введены корректно, то есть
не зависят от выбора элементов классов,
и совпадают с индуктивными определениями.
Основные свойства
Коммутативность сложения.
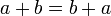
Коммутативность умножения.
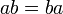
Ассоциативность сложения.
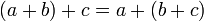
Ассоциативность умножения.
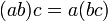
Дистрибутивность умножения относительно сложения.
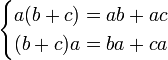
Расширение понятия числа — это новые определения для числовых выражений, не вычислимых в старой области значений, при «постоянстве формальных законов» (Hankel, 1867, §3.)
Например, среди натуральных чисел нет такого, которое означало бы половину, однако «половина», «середина отрезка», «равная пропорция» суть термины, вполне строго соответствующие операции деления единицы на двойку: 12. Обобщение этого построения до всех возможных значений выражения aba,b∈N — есть расширение понятия числа от натуральных N к неотрицательным рациональным Q≥0, при котором натуральные пропорции 1:1, 2:1 … n:1 суть частный случай: ∀a,b∈Nabb≡a=a1∈Q.
С другой стороны:
Отношение равенства позволяет определить ноль, как натуральное число, сумма которого с любым натуральным числом равна тому числу: 1+0=1, то есть нейтральный элемент («единица») по сложению.
На утверждении равенства двух выражений основан вычислительный приём уравнения.
Операция вычитания, — инверсия (обращение, «переворот») сложения: 1+1−1=1; 1−1=0. Вычитание большего числа из меньшего требует расширения системы до Z — алгебраического кольца целых чисел: 1−(1+1)=−1
Это простейшие примеры, однако, знак равенства =, отрицательные числа и ноль не употребляются классическими математиками Греции и Рима.
Логическая же невозможность точного дробного (рационального, Q) вычисления даже таких простых геометрических формализмов, как диагональ квадрата 2a−−√ или длина единичной окружности π — ведут к допущению иррациональных (или, соответственно, трансцендентных) чисел, не выразимых в конечных арифметических (или алгебраических) соотношениях, но, по факту их принадлежности континууму, состоящих во множестве действительных чисел R. В школьных учебниках те обычно представляются как бесконечные и допустимо апериодичные десятичные дроби.
Алгебраическое замыкание поля действительных чисел образует поле комплексных чисел С. Его можно представлять как поле действительных чисел и мнимой единицы i.
Примеры дальнейших расширений понятия числа: гиперкомплексные (начиная с кватернионов), трансфинитные, p-адические, сюрреальные…
Первоосновой всех этих объектов являются натуральные числа.
Числовая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения вматематическом анализе.
Пусть множество X —
это либо множество вещественных чисел ![]() ,
либо множество комплексных чисел
,
либо множество комплексных чисел ![]() .
Тогда последовательность
.
Тогда последовательность ![]() элементов
множества Xназывается числовой
последовательностью.
элементов
множества Xназывается числовой
последовательностью.
Примеры
Функция
 является
бесконечной последовательностью целых
чисел. Начальные отрезки этой
последовательности имеют вид
является
бесконечной последовательностью целых
чисел. Начальные отрезки этой
последовательности имеют вид 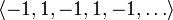 .
.Функция
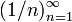 является
бесконечной последовательностью рациональных
чисел. Начальные отрезки этой
последовательности имеют вид
является
бесконечной последовательностью рациональных
чисел. Начальные отрезки этой
последовательности имеют вид 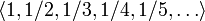 .
.Функция, сопоставляющая каждому натуральному числу
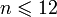 одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида
одно
из слов «январь», «февраль», «март»,
«апрель», «май», «июнь», «июль», «август»,
«сентябрь», «октябрь», «ноябрь»,
«декабрь» (в порядке их следования
здесь) представляет собой последовательность
вида 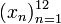 .
В частности, пятым членом x5 этой
последовательности является слово
«май».
.
В частности, пятым членом x5 этой
последовательности является слово
«май».
Операции над последовательностями
На множестве всех последовательностей элементов множества X можно определить арифметические и другие операции, если таковые определены на множестве X. Такие операции обычно определяют естественным образом, т. е. поэлементно.
-
Пусть на множестве X определена N-арная операция f:
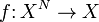
Тогда для элементов
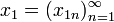 ,
, 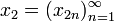 ,
…,
,
…, 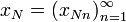 множества
всех последовательностей элементов
множества Xоперация f будет
определяться следующим образом:
множества
всех последовательностей элементов
множества Xоперация f будет
определяться следующим образом:
Например, так определяются арифметические операции для числовых последовательностей.
Суммой числовых последовательностей (xn) и (yn) называется числовая последовательность (zn) такая, что zn = xn + yn.
Разностью числовых последовательностей (xn) и (yn) называется числовая последовательность (zn) такая, что zn = xn − yn.
Произведением числовых
последовательностей xn и yn называется
числовая последовательность (zn) такая,
что ![]() .
.
Частным числовой
последовательности xn и
числовой последовательности yn,
все элементы которой отличны от нуля,
называется числовая последовательность  .
Если в последовательности yn на
позиции
.
Если в последовательности yn на
позиции ![]() всё
же имеется нулевой элемент, то результат
деления на такую последовательность
всё равно может быть определён, как
последовательность
всё
же имеется нулевой элемент, то результат
деления на такую последовательность
всё равно может быть определён, как
последовательность 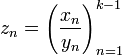 .
.
Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или дажекольца.
Подпоследовательности
Подпоследовательность последовательности (xn) —
это последовательность ![]() ,
где (nk) — возрастающая
последовательность элементов множества
натуральных чисел.
,
где (nk) — возрастающая
последовательность элементов множества
натуральных чисел.
Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.
Примеры
Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел.
Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.
Свойства
Всякая последовательность является своей подпоследовательностью.
Для всякой подпоследовательности
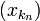 верно,
что
верно,
что 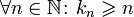 .
.
Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.
Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.
Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.
Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
Чи́сла Фибона́ччи — элементы числовой последовательности
