
- •Наивная теория множеств
- •Аксиоматическая теория множеств
- •Аксиомы Пеано
- •Теоретико-множественное определение (Определение Фреге-Рассела)
- •0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (Последовательность a000045 вOeis)
- •1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (Последовательность a001175 в oeis)
- •Обозначения
- •Основные свойства
- •Математическая модель
- •Доказательство
- •Свойства нок
- •Свойства нод
Доказательство
Обобщения теоремы
Если p простое число, а m и n — такие положительные целые числа, что
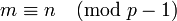 ,
тогда
,
тогда 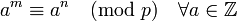 .
Это утверждение используется в системе
шифрования с открытым ключом RSA.
.
Это утверждение используется в системе
шифрования с открытым ключом RSA.Малая теорема Ферма является частным случаем теоремы Эйлера, которая, в свою очередь, является частным случаем теоремКармайкла и Лагранжа.
Малая теорема Ферма также имеет изящное обобщение в теории конечных полей.
Теорема Вильсона — теорема теории чисел, которая утверждает, что
p — простое число тогда и только тогда, когда (p − 1)! + 1 делится на p |
Практическое использование теоремы Вильсона для определения простоты числа нецелесообразно из-за сложности вычисленияфакториала.
Свойства нок
Коммутативность:
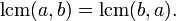
Ассоциативность:
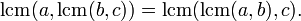
Связь с наибольшим общим делителем gcd(a,b):
![]()
В частности, если a и b — взаимно-простые числа, то:
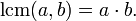
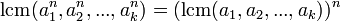 при
при
Наименьшее общее кратное двух целых чисел m и n является делителем всех других общих кратных m и n. Более того, множество общих кратных m, n совпадает с множеством кратных для НОК(m, n).
Асимптотики для
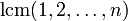 могут
быть выражены через
некоторые теоретико-числовые функции.
Так, функция Чебышёва
могут
быть выражены через
некоторые теоретико-числовые функции.
Так, функция Чебышёва 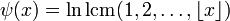 .
А также:
.
А также: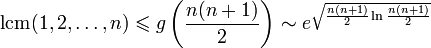 .
Это следует из определения и
свойств функции
Ландауg(n).
.
Это следует из определения и
свойств функции
Ландауg(n).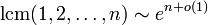 ,
что следует из закона
распределения простых чисел.
,
что следует из закона
распределения простых чисел.
Свойства нод
Основное свойство: наибольший общий делитель m и n делится на любой общий делитель этих чисел. Пример: для чисел 12 и 18 наибольший общий делитель равен 6; он делится на все общие делители этих чисел: 1, 2, 3, 6.
Следствие 1: множество общих делителей m, n совпадает с множеством делителей НОД(m, n).
Следствие 2: множество общих кратных m, n совпадает с множеством кратных НОК(m, n).
Если m делится на n, то НОД(m, n) = n. В частности, НОД(n, n) = n.
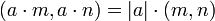 —
общий множитель можно выносить за знак
НОД.
—
общий множитель можно выносить за знак
НОД.Если D = (m,n), то после деления на D числа становятся взаимно простыми, то есть,
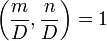 .
Это означает, в частности, что для
приведения дроби к
несократимому виду надо разделить
её числитель и знаменатель на
их НОД.
.
Это означает, в частности, что для
приведения дроби к
несократимому виду надо разделить
её числитель и знаменатель на
их НОД.Мультипликативность: если a1,a2 взаимно просты, то:
![]()
Наибольший общий делитель чисел m и n может быть определён как наименьший положительный элемент множества всех ихлинейных комбинаций:
![]()
и поэтому (m,n) представим в виде линейной комбинации чисел m и n:
![]() .
.
Это соотношение
называется соотношением
Безу, а коэффициенты u и v — коэффициентами
Безу. Коэффициенты Безу эффективно
вычисляются расширенным
алгоритмом Евклида. Это
утверждение обобщается на наборы
натуральных чисел — его смысл в том,
что подгруппа группы ![]() ,
порождённая набором
,
порождённая набором ![]() , — циклическая и
порождается одним элементом: НОД
, — циклическая и
порождается одним элементом: НОД![]() .
.
Свойства Арифм. прогрессии
Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии:
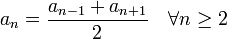 .
.Обратное также верно, то есть это свойство является признаком арифметической прогрессии.
Доказательство:
![]()
![]() аналогично
аналогично
Сумма n первых членов арифметической прогрессии может быть выражена формулами
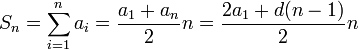
Доказательство:
Через сумму:
![]()
![]()
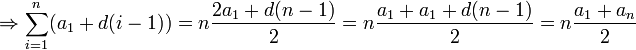
По индукции:
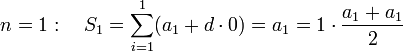
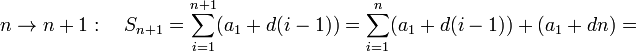
![]()
![]()
Сумма n последовательных членов арифметической прогрессии начиная с члена k:
![]()
Пример суммы арифметической прогрессии является сумма ряда натуральных чисел до n включительно:
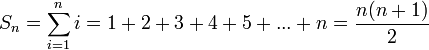
Произведение членов арифметической прогрессии выражается через Гамма-функцию.
Свойства геометр. прогрессии
Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию
Доказательство[скрыть]
Пусть wn —
последовательность : ![]()
![]()
![]()
Полученное соотношение является характеристическим для арифметической прогрессии.
Доказательство[скрыть]
![]()
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
![]() ,
,
Доказательство[скрыть]
![]()
Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
![]()
Доказательство[скрыть]

Сумма n первых членов геометрической прогрессии:
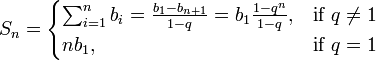
Доказательство[скрыть]
Через сумму:
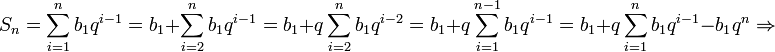
![]()
Индукцией по n:
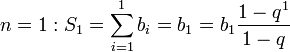
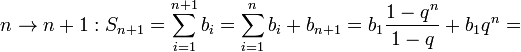
![]()
Если
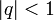 ,
то
,
то 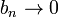 при
при 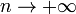 ,
и
,
и
![]() при
.
при
.
Основные свойства пропорций
Обращение пропорции. Если
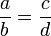 ,
то
,
то 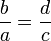
Перемножение членов пропорции крест-накрест. Если , то
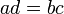
Перестановка средних и крайних членов. Если , то
![]() (перестановка
средних членов пропорции),
(перестановка
средних членов пропорции),
![]() (перестановка
крайних членов пропорции).
(перестановка
крайних членов пропорции).
Увеличение и уменьшение пропорции. Если , то
![]() (увеличение
пропорции),
(увеличение
пропорции),
![]() (уменьшение
пропорции).
(уменьшение
пропорции).
Составление пропорции сложением и вычитанием. Если , то
![]() (составление
пропорции сложением),
(составление
пропорции сложением),
![]() (составление
пропорции вычитанием).
(составление
пропорции вычитанием).
