Аксиоматическая теория множеств

Особенностью аксиоматического подхода является отказ от лежащего в основе программы Кантора представления о действительном существовании множеств в некотором идеальном мире. В рамках аксиоматических теорий множества «существуют» исключительно формальным образом, и их «свойства» могут существенно зависеть от выбора аксиоматики. Этот факт всегда являлся мишенью для критики со стороны тех математиков, которые не соглашались (как на том настаивал Гильберт) признать математику лишённой всякого содержания игрой в символы. В частности, Н. Н. Лузин писал, что «мощность континуума, если только мыслить его как множество точек, есть единая некая реальность», место которой в ряду кардинальных чисел не может зависеть от того, признаётся ли в качестве аксиомы континуум-гипотеза, или же её отрицание.

В настоящее время наиболее распространённой аксиоматической теорией множеств является ZFC — теория Цермело — Френкеля саксиомой выбора. Вопрос о непротиворечивости этой теории (а тем более — о существовании модели для неё) остаётся нерешённым.

Не всеми математиками аксиома выбора принимается безоговорочно. Так, например Эмиль Борель и Анри Лебег считают, что доказательства, полученные при помощи этой аксиомы, имеют другую познавательную ценность, чем доказательства, независимые от неё. Другие же математики, такие как Феликс Хаусдорф и Адольф Френкель, принимают аксиому выбора безоговорочно, признавая за ней ту же степень очевидности, что и за другими аксиомами Цермело — Френкеля.^[2]

Основные понятия

В основе теории множеств лежат первичные понятия: множество и отношение быть элементом множества (обозначается как  ^[3] — «x есть элемент множества A»). Среди производных понятий наиболее важны следующие:

• пустое множество;

• подмножество и надмножество;

• семейство множеств;

• пространство (Универсум);

• конституента.

Над множествами определены следующие операции:

• объединение (или сумма) (обозначается как  );

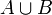• разность (обозначается как   реже  );

• дополнение (обозначается как   или  );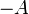

• пересечение (или произведение) (обозначается как  );

• симметрическая разность (обозначается как 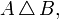  реже  ).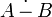

Для множеств определены следующие бинарные отношения:

• отношение равенства (обозначается как  );

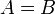• отношение включения (обозначается как  ).

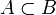Операции над множествами

[править]Бинарные операции

Ниже перечислены основные операции над множествами:

• пересечение:

• объединение:

Если множества A и B не пересекаются:  , то их объединение обозначают также:  .

• разность (дополнение):

• симметрическая разность:

• Декартово или прямое произведение:

Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.

[править]Унарные операции

• Абсолютное дополнение:

Операция дополнения подразумевает некоторый универсум (универсальное множество U, которое содержит A):

Относительным же дополнением называется А\В (см.выше):

• Мощность множества:

| A |

Результатом является кардинальное число (для конечных множеств — натуральное).

• Множество всех подмножеств (булеан):

Обозначение происходит из того, что   в случае конечных множеств.

Числовые множества. Мы будем рассматривать следующие числовые множества, которые нам будут встречаться.

N - множество натуральных чисел. Это числа вида один, два, три и т. д. Мы не будем специально определять, что такое натуральное число.

Множество целых чисел Z, это числа ноль, один, минус один, два, минус два и т. д. То есть мы к натуральным числам добавляем ноль и отрицательные числа.

Q - множество рациональных чисел. Это числа вида M деленное на N, где M и N целые и N отличное от нуля. Рациональные числа могут быть записаны так же в виде десятичных дробей, при помощи известной операции деления. В результате деления будет получаться либо конечные дроби, либо периодические.

Например: одна двадцать пятая равна ноль целых четыре сотых, одна третья равна ноль целых и бесконечная цепочка троек или как говорят три в периоде. Кратко можно написать как ноль целых, запятая и три в скобках. Пять шестых рaвняется ноль целых восемь и три в периоде.

Числа, которые невозможно представить в виде m делённое на n, где m и n целые числа, называются иррациональными. Иррациональные числа не представляются в виде конечных десятичных дробей или в виде бесконечной периодической дроби. Например, число пи или корень из двух.

Дальше множество действительных чисел. Ее можно определить как множество десятичных дробей как периодических, так и непериодических. Непериодические бесконечные десятичные дроби называют иррациональными числами.

Действительные числа можно изображать в виде точек на числовой прямой. Для этого нужно взять прямую, отметить на ней точку, которой будет соответствовать число ноль - точка отсчета, выбрать единичный отрезок, то есть отметить некоторую точку числом единица и при этом мы уже на прямой выбираем положительное направление. Предположим мы отметили точку соотвествующую единице справа от нуля. С той стороны, где стоит единица, это направление считается положительным.

Слева от нуля будут отрицательные числа,

а справа от нуля - положительные.

Каждой точке А на этой прямой соответствует число, которая определяется так: находим длину отрезка ОА, принимая за единицу измерения отрезок от нуля до единицы

и эту длину называем координатой точки А и это число приписываем точке А. Если точка взята справа, то число берем с плюсом, а если слева, то берем с минусом.

Для действительных чисел определяется модуль.

Модуль числа Х обозначается так, он по определению равен Х, если Х больше или равно нуля и минус Х, если Х меньше нуля. Например: модуль пяти равен пяти, модуль минус трех равен трем,

то есть для пяти мы используем первую строчку, так как пять больше нуля а для минус трех используем вторую строчку, так как минус три меньше нуля.

В этом случае нужно поменять знак Х, то есть отбросить минус. Геометрический смысл:

модуля Х можно рассматривать как расстояние от точки А с координатой Х до начала координат.

Натуральные числа можно использовать для счёта (одно яблоко, два яблока и т. п.).

Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).

Существуют два подхода к определению натуральных чисел — числа, используемые при:

• перечислении (нумеровании) предметов (первый, второй, третий, …);

• обозначении количества предметов (нет предметов, один предмет, два предмета, …). Принят в трудах Бурбаки, где натуральные числа определяются как мощностиконечных множеств.

Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются.

Множество всех натуральных чисел принято обозначать знаком  . Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.