
- •Наивная теория множеств
- •Аксиоматическая теория множеств
- •Аксиомы Пеано
- •Теоретико-множественное определение (Определение Фреге-Рассела)
- •0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (Последовательность a000045 вOeis)
- •1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (Последовательность a001175 в oeis)
- •Обозначения
- •Основные свойства
- •Математическая модель
- •Доказательство
- •Свойства нок
- •Свойства нод
1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (Последовательность a001175 в oeis)
В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
Натуральное число N является числом Фибоначчи тогда и только тогда, когда 5N2 + 4 или 5N2 − 4 является квадратом.[4]
Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[5]
Последовательность Фарея n-ного порядка представляет собой возрастающий ряд всех несократимых дробей, знаменатель которых меньше или равен n:
![]()
Последовательность Фарея порядка n + 1 можно построить из последовательности порядка n по следующему правилу:
Копируем все элементы последовательности порядка n.
Если сумма знаменателей в двух соседних дробях последовательности порядка n дает число не большее, чем n + 1, вставляем между этими дробями их медианту, равную отношению суммы их числителей к сумме знаменателей.
Пример
Последовательности Фарея для n от 1 до 8:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Свойства
-
Если p1 / q1 < p2 / q2 — две соседние дроби в ряде Фарея, тогда q1p2 − q2p1 = 1.
Доказательство. Заметим,
что треугольник на плоскости с
вершинами ![]() ,
, ![]() и
и ![]() не
может содержать целых точек, отличных
от вершин. Иначе, если целая точка
не
может содержать целых точек, отличных
от вершин. Иначе, если целая точка ![]() содержится
в
содержится
в ![]() ,
то дробь r / s лежит
между p1 / q1 и p2 / q2,
а знаменатель s не превосходит
,
то дробь r / s лежит
между p1 / q1 и p2 / q2,
а знаменатель s не превосходит ![]() .
Значит, по формуле
Пика, его площадь равна 1 / 2.
С другой стороны, площадь
равна (q1p2 − q2p1)
/ 2. Ч.
т. д.
.
Значит, по формуле
Пика, его площадь равна 1 / 2.
С другой стороны, площадь
равна (q1p2 − q2p1)
/ 2. Ч.
т. д.
Справедливо и обратное
утверждение: если дроби p1 / q1 < p2 / q2 таковы,
что q1p2 − q2p1 =
1, то они представляют собой соседние
члены ряда Фарея ![]() .
.
Дели́мость — одно из основных понятий арифметики и теории чисел, связанное с операцией деления. С точки зрения теории множеств, делимость целых чисел является отношением, определённым на множестве целых чисел.
Если для некоторого целого числа a и целого числа b существует такое целое число q, что bq = a, то говорят, что число a делится нацело на b или, что b делит a.
При этом число b называется делителем числа a, делимое a будет кратным числа b, а число q называется частным от деления aна b.
Хотя свойство делимости определено на всём множестве целых чисел, обычно рассматривается лишь делимость натуральныхчисел. В частности, функция количества делителей натурального числа подсчитывает лишь его положительные делители.
Обозначения
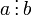 означает,
что a делится на b
означает,
что a делится на bb | a или b \ a означает, что b делит a, или, что то же самое: b — делитель a.
Свойства
Замечание: во
всех формулах этого раздела предполагается,
что ![]() —
целые числа.
—
целые числа.
Любое целое число является делителем нуля, и частное равно нулю :
![]()
Любое целое число делится на единицу:
![]()
На ноль делится только ноль:
![]() ,
,
причём частное в этом случае не определено.
Единица делится только на единицу:
![]()
Для любого целого числа
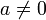 найдётся
такое целое число
найдётся
такое целое число 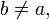 для
которого
для
которого 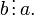
Если и
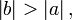 то
то 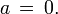 Отсюда
же следует, что если
и
то
Отсюда
же следует, что если
и
то 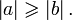
Для того чтобы необходимо и достаточно, чтобы
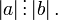
Если
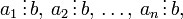 то
то 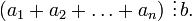
Свойство делимости является отношением нестрогого порядка и, в частности, оно:
рефлексивно, т.е. любое целое число делится на себя же:
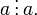
транзитивно, т.е. если и
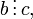 то
то 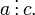
антисимметрично, т.е. если и
 то
либо
то
либо 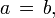 либо
либо 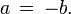
Множество рациональных чисел
Множество рациональных
чисел обозначается ![]() и
может быть записано в виде:
и
может быть записано в виде:
![]()
Нужно понимать, что
численно равные дроби, например, ![]() и
и ![]() ,
входят в это множество как одно число.
Поскольку делением числителя и знаменателя
дроби на ихнаибольший
общий делитель можно получить
единственное несократимое представление
рационального числа, то можно говорить
об их множестве как о множестве несократимых дробей
со взаимно
простыми целым числителем
и натуральным знаменателем:
,
входят в это множество как одно число.
Поскольку делением числителя и знаменателя
дроби на ихнаибольший
общий делитель можно получить
единственное несократимое представление
рационального числа, то можно говорить
об их множестве как о множестве несократимых дробей
со взаимно
простыми целым числителем
и натуральным знаменателем:
![]()
Здесь gcd(m,n) — наибольший общий делитель чисел m и n.
Множество рациональных
чисел является естественным обобщением
множества целых
чисел. Легко видеть, что если у
рационального числа ![]() знаменатель n =
1, то a = m является
целым числом. В этой связи возникают
некоторые обманчивые предположения.
Однако, хотя кажется, что рациональных
чисел больше чем целых, и тех и
других счётное
число (то есть оба они могут
быть перенумерованы
натуральными числами, причём
явно).
знаменатель n =
1, то a = m является
целым числом. В этой связи возникают
некоторые обманчивые предположения.
Однако, хотя кажется, что рациональных
чисел больше чем целых, и тех и
других счётное
число (то есть оба они могут
быть перенумерованы
натуральными числами, причём
явно).
