Доказательство теоремы
Рассмотрим
произвольные векторы ядра линейного
оператора:
и
.
Это означает:
и
.
A
— линейный оператор, следовательно,
т.е.
;
для любого числа
,
т.е.
.
Теорема доказана.
Определение. Размерность ядра линейного оператора называется дефектом оператора, обозначается def(A): r=def(A)=dimKer(A).
Примеры.
Ядро и образ нулевого
оператора: поскольку
то
ядро
и образ тождественного (единичного)
оператора: поскольку
,
то
Билет 26
Линейный оператор. Матрица линейного оператора в заданных (заданном) базисах.
Определение. Если каждому элементу из пространства Rn ставится в соответствие единственный элемент из пространства Rm , то говорят, что задан оператор, действующий из пространства Rn в пространство Rm (или оператор, действующий в пространстве Rn, если n=m).
Результат действия оператора A на элемент обозначают .
Если элементы и связаны соотношением , то называют образом ; а — прообразом .
Множество элементов пространства Rn, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A).
Множество элементов пространства Rm, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если , то
Ядром оператора называется множество элементов линейного пространства Rn, образом которых является нулевой элемент. Ядро оператора обозначают Ker(A): .
Определение. Оператор A, действующий из пространства Rn в пространство Rm называется линейным оператором, если для любых из Rn и для любого действительного числа α справедливо:
и .
Определение. Матрица, столбцами которой являются координаты образов базисных векторов некоторого базиса в Rт —
называется матрицей линейного оператора A в заданных базисах.
Обратите внимание,
теперь и в дальнейшем A
(полужирная) — обозначение линейного
оператора, A(светлая)
или Aef
— обозначение матрицы оператора A
в некоторых базисах или в базисе
и
.
Таким образом, доказана следующая теорема.
Теорема (связь
координат образа и прообраза). Если в
пространствах Rn
и Rm
определены некоторые базисы
и
,
,
— и
,
то векторы-столбцы их координат
и
в этих базисах связаны соотношением
,
где A — матрица
оператора A
в этих базисах.
Между множеством линейных операторов, действующих из пространства Rn в пространство Rm , и множеством прямоугольных матриц размерности m, n можно установить взаимно однозначное соответствие.
Примеры
1.
Матрица нулевого оператора:
поскольку
то
и, следовательно, матрица нулевого
оператора — нулевая матрица.
2.
Матрица тождественного (единичного)
оператора: поскольку
,
то
(единица на i-м месте)
и, следовательно, матрица тождественного
оператора — единичная матрица.
3.
Матрица оператора проектирования
пространства R3
на подпространство R2
параллельно вектору
:
поскольку
,
то у матрицы P оператора
проектирования последний столбец —
нулевой; она имеет вид
.
Билет 27
Преобразование координат вектора при изменении базиса
Как
уже отмечалось, в n-мерном
пространстве Rn
существует множество различных
базисов. Пусть
и
—
два базиса в Rn.
Обозначим
и
координаты вектора
в базисах
и
(векторы-столбцы!!!),
т.е.
,
,
,
.
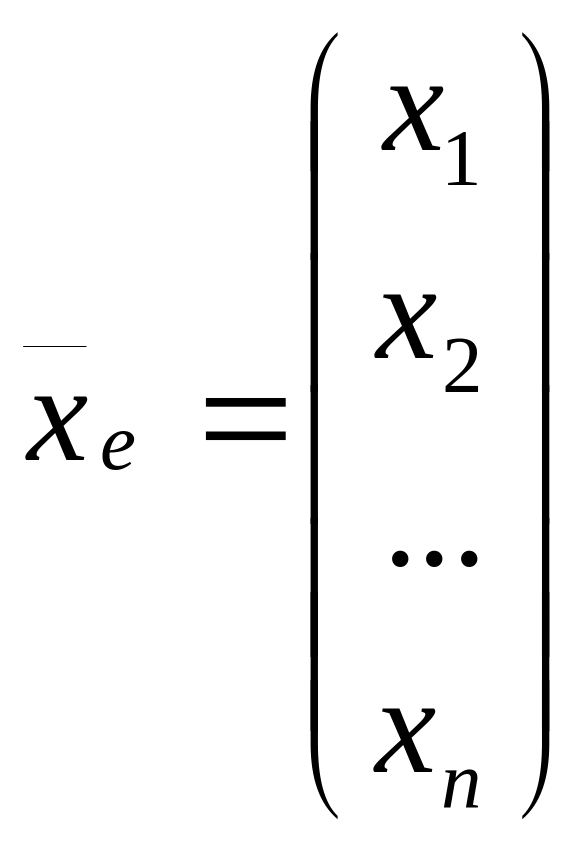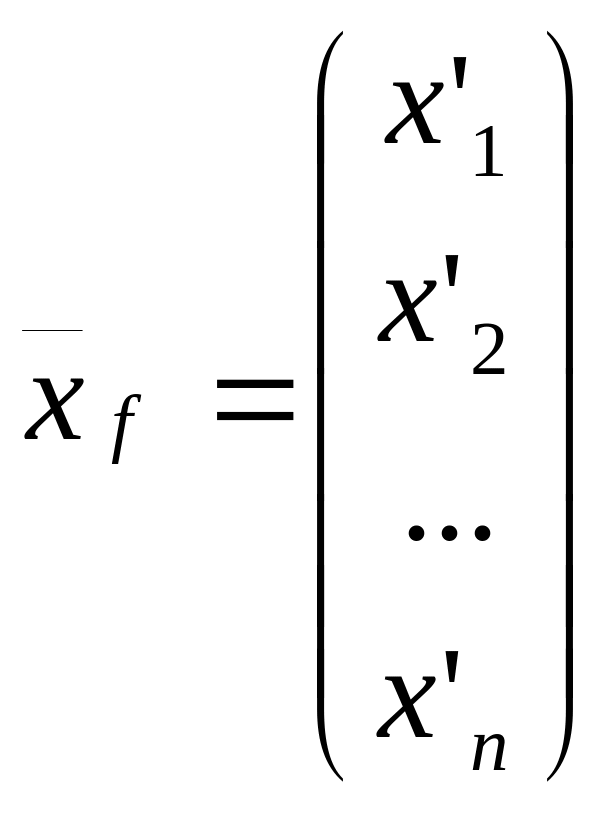Естественно,
существует связь между координатами
вектора в разных базисах. Найдем ее.
Поскольку векторы
базиса
сами
являются векторами из Rn,
их можно разложить по базису
:
.
Тогда
,
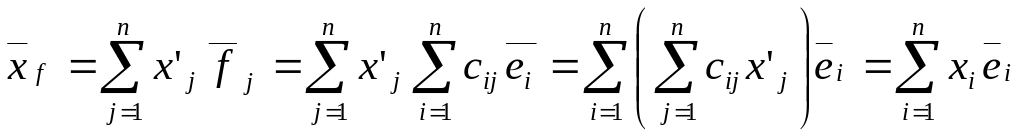т.е.
или, что то же самое,
,
.
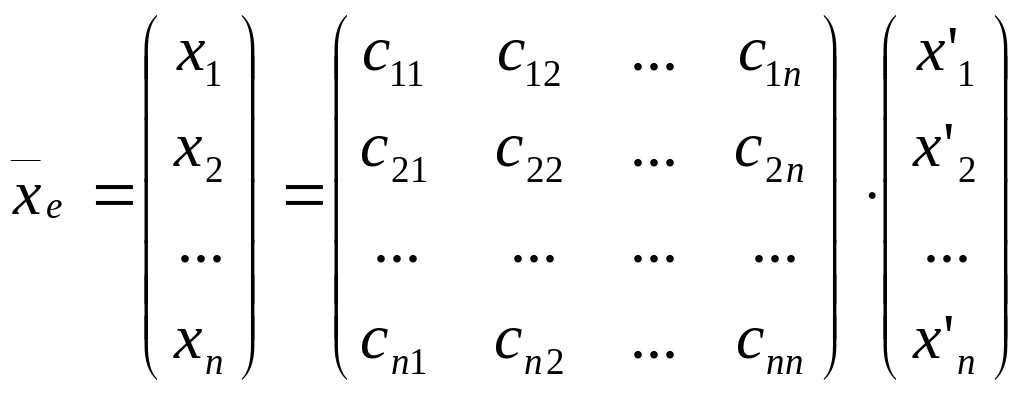Определение.
Матрица
называется матрицей перехода от базиса
к базису
,
это матрица, столбцами которой являются
координаты базисных векторов
(«новых» базисных векторов) в базисе
(в
«старом» базисе).
Матрица перехода обратима. Действительно, ее столбцы линейно независимы, поскольку они — координатные столбцы базисных векторов.
Тогда
из
имеем формулу преобразования координат
вектора при изменении базиса:
.
Билет 28
Преобразование матрицы линейного оператора при изменении базиса
Пусть и — два базиса в Rn.
Обозначим
и
координаты векторов
и
из Rn
и матрицу оператора A
соответственно в базисах
и
,
а
—
матрицу перехода от базиса
к
базису
,
т.е.
,
,
Тогда
откуда имеем
формулы преобразования матрицы линейного
оператора при изменении базиса:
.
Билет 29
Собственные значения и собственные векторы линейного оператора. Характеристическое уравнение.
Определение.
Пусть A
— линейный оператор, действующий в
линейном пространстве Rn.
Число
называется собственным значением, а
ненулевой вектор
из
Rn
— соответствующим собственным вектором
линейного оператора A,
если они связаны между собой соотношением.
.
Примеры.
1. Нулевой
оператор
:
,
т.е.
— собственное значение нулевого
оператора, а соответствующие собственные
векторы — все ненулевые векторы
пространства Rn.
2. Тождественный
(единичный) оператор I:
— т.е.
собственное значение тождественного
оператора, а соответствующие собственные
векторы — все ненулевые векторы
пространства Rn.
3.
Оператор P2
— оператор проектирования пространства
R3 на
подпространство R2
параллельно вектору
:
,
,
т.е.
— собственное значение оператора,
проектирования, а соответствующие
собственные векторы — все ненулевые
векторы R3,
третья координата которых равна нулю:
.
Пусть A— матрица оператора в некотором базисе в Rn.
Собственные
значения оператора и соответствующие
им собственные векторы связаны
соотношением
или, что то же самое,
:
,
. Здесь
—
единичный оператор.
По теореме о связи
координат образа и прообраза имеем:
,
где E — единичная
матрица, а
— нулевой вектор Rn
.
Это означает, что
собственный вектор оператора является
ненулевым решением линейной однородной
системы
.
Ненулевое решение однородной системы
(система нетривиально совместна),
существует тогда и только тогда, когда
определитель матрицы системы равен
нулю:
.
Следовательно, собственные значения
линейного оператора могут быть вычислены
как корни уравнения
,
а собственные векторы — как решения
соответствующих однородных систем.
Легко видеть, что
определитель
—
многочлен n-й
степени относительно
.
Определение. Уравнение называется характеристическим уравнением оператора, а многочлен — характеристическим многочленом оператора
Билет 30
Собственные значения и собственные векторы линейного оператора. Свойства собственных векторов. Доказать, что собственные векторы, отвечающие различным собственным значениями линейно независимы.
Определение. Пусть A — линейный оператор, действующий в линейном пространстве Rn. Число называется собственным значением, а ненулевой вектор из Rn — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением. .
Примеры.
1. Нулевой оператор : , т.е. — собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
2. Тождественный (единичный) оператор I: — т.е. собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
3. Оператор P2 — оператор проектирования пространства R3 на подпространство R2 параллельно вектору : , , т.е. — собственное значение оператора, проектирования, а соответствующие собственные векторы — все ненулевые векторы R3, третья координата которых равна нулю: .
Пусть A— матрица оператора в некотором базисе в Rn.
Собственные значения оператора и соответствующие им собственные векторы связаны соотношением или, что то же самое, :
, . Здесь — единичный оператор.
Свойства собственных векторов
Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:
характеристический многочлен оператора, действующего в Rn является многочленом n-й степени относительно ;
линейный оператор, действующий в Rn, имеет не более n различных собственных значений;
собственные векторы оператора определяются с точностью до постоянного сомножителя; поэтому принять вычислять собственные векторы единичной длины — орты собственных векторов;
докажем, что если
— собственный вектор линейного оператора
A, отвечающий собственному
значению
,
то для любого отличного от нуля числа
вектор
(
)—
собственный вектор оператора A,
отвечающий собственному значению
:
;
корни характеристического многочлена не зависят от базиса;
собственные векторы, отвечающие различным собственным значениям, линейно независимы.
Докажем линейную независимость собственных векторов, отвечающих различным собственным значениям.
Пусть
— собственный вектор линейного оператора
A, отвечающий собственному
значению
,
а
— собственный вектор линейного оператора
A, отвечающий собственному
значению
,
:
и
.
Предположим, что
векторы
и
линейно зависимы. Это означает, что один
из них линейно выражается через другой:
существует такое число
,
что
.
Тогда:
.