Доказательство теоремы
Необходимость.
Система
нетривиально совместна. Это означает,
что существуют числа
не все равные нулю, для которых справедливо
.
Последнее равенство означает, что n
столбцов матрицы систем линейно
зависимы и, следовательно, ранг матрицы
системы (максимальное число линейно
независимых столбцов) меньше числа
столбцов, меньше числа неизвестных.
Необходимость доказана.
Достаточность.
Пусть ранг r матрицы
системы меньше числа n
неизвестных. По теореме о базисном
миноре из этого следует, что существует
отличный от нуля минор матрицы порядка
r. Не умаляя общности,
будем полагать, что базисный минор —
главный минор матрицы
Базисные
переменные можно вычислить по формулам
Крамера
,
i = 1, 2, …, r
.
Тогда
вектор
—
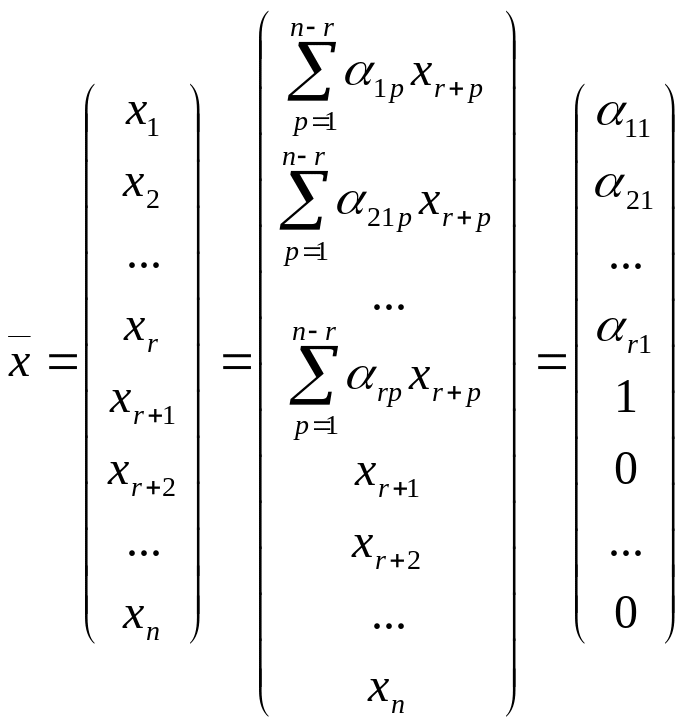отличное от тождественного нуля решение
однородной системы
.
Т.е. однородная система нетривиально
совместна. Теорема доказана.
Билет 21
Однородная система линейных алгебраических уравнений. Фундаментальная система решений
Напомним, что система линейных уравнений может быть записана в матричной форме:
,
где
—
матрица системы,
—
правая часть,
—
искомое решение,
Определение. Если правая часть системы равна нулю, то система называется однородной.
Если и — два решения однородной системы , то при любых действительных числах α и β вектор — решение системы .
Пусть
и
— два решения системы
,
т. е.
и
и пусть α и β
любые действительные числа. Тогда
,
т.е. вектор
— решение однородной системы.
Определение.
Система
,
состоящая из n-r
линейно независимых решений однородной
системы
,
,
RgA=r
, называется фундаментальной
системой решений однородной
системы.
Билет 22
Однородная система линейных алгебраических уравнений. Структура общего решения.
Напомним, что система линейных уравнений может быть записана в матричной форме:
,
где — матрица системы, — правая часть, — искомое решение,
Определение. Если правая часть системы равна нулю, то система называется однородной.
Если и — два решения однородной системы , то при любых действительных числах α и β вектор — решение системы .
Пусть и — два решения системы , т. е. и и пусть α и β любые действительные числа. Тогда , т.е. вектор — решение однородной системы.
Определение. Выражение, позволяющее вычислить все (любое) решения системы, называется общим решением системы.
Билет 23
Неоднородная система линейных алгебраических уравнений. Структура общего решения.
Напомним, что система линейных уравнений может быть записана в матричной форме:
,
где — матрица системы, — правая часть, — искомое решение,
Определение. Если правая часть системы не равна нулю, то система называется неоднородной.
Если и — два решения неоднородной системы , то вектор — решение приведенной однородной системы однородной .
Если решение неоднородной системы , а — решение однородной системы , то вектор — решение неоднородной системы .
Структура общего решения неоднородной системы
Вспомним одно из свойств решений линейной неоднородной системы:
Если и — два решения системы , то вектор — решение приведенной однородной системы .
Поскольку выражение
задает все решения однородной
системы, то для любых двух решений
и
неоднородной системы справедливо
и, следовательно,
выражение
позволяет вычислить любое решение
неоднородной системы.
Билет 24
Линейный оператор. Определение. Примеры
Определение. Если каждому элементу из пространства Rn ставится в соответствие единственный элемент из пространства Rm , то говорят, что задан оператор, действующий из пространства Rn в пространство Rm (или оператор, действующий в пространстве Rn, если n=m).
Результат действия
оператора A на элемент
обозначают
.
Если элементы и связаны соотношением , то называют образом ; а — прообразом .
Множество элементов пространства Rn, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A).
Множество элементов
пространства Rm,
которые являются образами элементов
из области определения D(A)
оператора A, называют
образом оператора A
и обозначают Im(A).
Если
,
то
Ядром оператора
называется множество элементов линейного
пространства Rn,
образом которых является нулевой
элемент. Ядро оператора обозначают
Ker(A):
.
Определение.
Оператор A,
действующий из пространства Rn
в пространство Rm
называется линейным оператором,
если для любых
из Rn
и для любого действительного числа α
справедливо:
и
.
Примеры
1.
Нулевой оператор
:
— линейный оператор, D()=Rn,
,
Ker()=Rn.
Докажем линейность нулевого оператора:
;
.
2.
Тождественный (единичный) оператор I:
— линейный оператор, D(I)=
Rn,
Im(I)=
Rn,
.
Докажем линейность тождественного оператора:
;
.
3.
Оператор P2
— оператор проектирования пространства
R3 на
подпространство R2
параллельно вектору
:
линейный оператор, D(P2)=
R3 R3,
Im(P2)=
R2,
.
Билет 25
Линейный оператор. Ядро линейного оператора. Примеры
Определение. Если каждому элементу из пространства Rn ставится в соответствие единственный элемент из пространства Rm , то говорят, что задан оператор, действующий из пространства Rn в пространство Rm (или оператор, действующий в пространстве Rn, если n=m).
Результат действия оператора A на элемент обозначают .
Если элементы и связаны соотношением , то называют образом ; а — прообразом .
Множество элементов пространства Rn, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A).
Множество элементов пространства Rm, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если , то
Ядром оператора называется множество элементов линейного пространства Rn, образом которых является нулевой элемент. Ядро оператора обозначают Ker(A): .
Определение. Оператор A, действующий из пространства Rn в пространство Rm называется линейным оператором, если для любых из Rn и для любого действительного числа α справедливо:
и .
Нулевой оператор : — линейный оператор, D()=Rn, , Ker()=Rn.
Докажем линейность нулевого оператора:
;
.
Определение.
Ядром линейного оператора
называется множество элементов
пространства Rn,
образом которых является нулевой
элемент. Ядро оператора обозначают
Ker(A):
.
Теорема. Ядро линейного оператора — линейное подпространство пространства Rn.